卡爾曼濾波在智駕中套用廣泛,從傳感器檢測的跟蹤到多傳感器的資訊融合,從單一傳感器定位資訊的濾波到多傳感器融合定位,從傳統檢測演算法到深度學習的後處理,都少不了卡爾曼濾波的身影。本文以基礎卡爾曼濾波器的套用舉例,試圖從整體框架和套用方面對卡爾曼濾波有個整體的理解,解決如何使用和使用過程中數據的分析解讀問題。
1. 整體介紹
全文以激光雷達對一個行人的檢測結果為輸入數據,構建卡爾曼濾波器對其檢測結果進行濾波,調整關鍵參數,直觀感受關鍵參數對濾波結果的影響。整體思路如下:
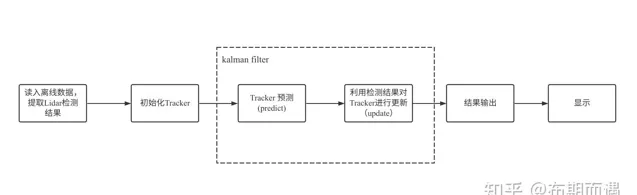
該開源數據中包含激光雷達和毫米波雷達兩個傳感器同時檢測的結果,因此需要從中提取出Lidar的檢測。通常我們detect或measurement來表示傳感器的檢測,用tracker表示經過卡爾曼濾波後跟蹤或濾波的結果。基卡爾曼濾波總體可以分為兩個部份:predict和update。其中predict接收上一時刻的tracker,將其預測到當前時刻下;update 接收measurement對predict得到的tracker進行更新,具體後面會詳細介紹。
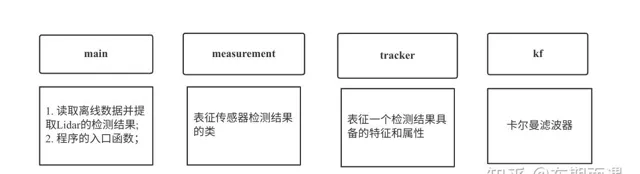
如圖2所示,文中會涉及到四個檔或類,分別是:函數的入口main, 處理檢測的measurement, 處理檢測結果的tracker, 進行濾波的kf。
2. 數據匯入
數據保存在 obj_pose-laser-radar-synthetic-input.txt 中 [1] ,一個行人在前面行走,一輛搭載了激光雷達和毫米波雷達的智能車輛對其進行持續的檢測。數據如圖3所示,該數據中包含了激光雷達和毫米波雷達的檢測結果,第一列的L表示該行是Lidar的數據,R表示行是Radar的數據。每行的第二列為傳感器檢測到的目標X座標,第三列為Y座標,第二列之後的數據本文暫不使用。

/* 以下為main.cpp的匯入數據部份 */
// 路徑為放置obj_pose-laser-radar-synthetic-input.txt檔的路徑
std
::
string
file_name
=
"obj_pose-laser-radar-synthetic-input.txt"
;
std
::
ifstream
in_file
(
"路徑/obj_pose-laser-radar-synthetic-input.txt"
);
if
(
!
in_file
.
is_open
())
{
std
::
cout
<<
"can not open input file: "
<<
file_name
<<
std
::
endl
;
}
int
i
=
0
;
std
::
string
one_line
;
// measurement類用於存放檢測結果,每一個檢測由時間戳timestamp,傳感器類別sensor_type,檢測數據x,y組成
std
::
vector
<
Measurement
>
measurement_list
;
// 每次讀取一行數據,其中i用於控制讀取數據的行數
while
(
getline
(
in_file
,
one_line
)
&&
(
i
<=
10
))
{
std
::
istringstream
iss
(
one_line
);
Measurement
one_frame_data
;
std
::
string
current_sensor
;
// 讀取一行中的第一個數據,也就是R或L
iss
>>
current_sensor
;
// 僅使用L的數據
if
(
current_sensor
.
compare
(
"L"
)
==
0
)
{
//一個檢測的sensor_type
one_frame_data
.
sensor_type_
=
Measurement
::
lidar
;
float
x
;
float
y
;
iss
>>
x
;
iss
>>
y
;
one_frame_data
.
sensor_measurment_
=
Eigen
::
VectorXd
(
2
);
// 一個檢測xy座標,構成一個二維的向量
one_frame_data
.
sensor_measurment_
<<
x
,
y
;
// 一個檢測的時間戳
iss
>>
one_frame_data
.
timestamp_
;
// 將整幀數據放到所有的測量中
measurement_list
.
push_back
(
one_frame_data
);
}
else
if
(
current_sensor
.
compare
(
"R"
)
==
0
)
{
continue
;
}
// i++; //當需要控制讀取行數時開啟
}
3.單幀數據的處理
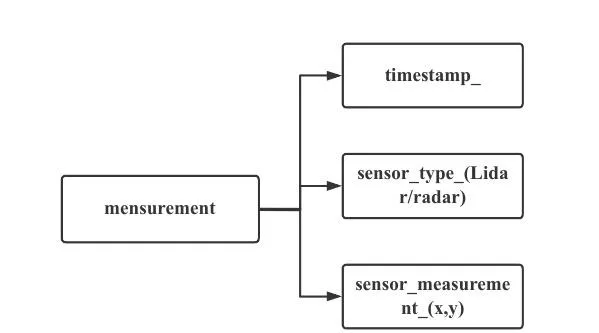
讀取的一幀幀數據依次存放到measurement_list中,每一幀的數據格式如圖4所示。
/* measurement.h */
#ifndef MEASUREMENT_H_
#define MEASUREMENT_H_
#include<stdint.h>
#include"Eigen/Dense"
class Measurement
{
public:
int64_t timestamp_;
enum SensorType
{
lidar,
radar
}sensor_type_;
Eigen::VectorXd sensor_measurment_;
};
#endif
下面對每一幀的數據進行處理,除第一次處理需要初始化外,其他幀直接進入處理過程,處理過程主要由predict和update兩步組成。
(1)tracker的初始化
tracker的初始化只在第一幀時發生,主要分為兩個部份,一個是卡爾曼濾波器相關參數的初始化,該類參數不依賴檢測數據,可直接在tracker新建的時候直接生成,例如測量矩陣H,狀態共變異數矩陣P,測量雜訊矩陣R,狀態轉移矩陣F; 第二類是與檢測相關的狀態參數,狀態量x,y,time_stamp.
tracker::tracker(){
kf_filer_.H_ = Eigen::MatrixXd(2,4);
kf_filer_.H_<< 1, 0, 0, 0,
0, 1, 0, 0;
kf_filer_.P_ = Eigen::MatrixXd(4,4);
kf_filer_.P_ << 1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1000, 0,
0, 0, 0, 1000;
kf_filer_.X_ = Eigen::VectorXd(4);
kf_filer_.R_ = Eigen::MatrixXd(2,2);
// kf_filer_.R_ << 0.0225, 0,
// 0, 0.0225;
kf_filer_.R_ << 2, 0,
0, 2;
kf_filer_.F_ = Eigen::MatrixXd(4,4);
state_.timestamp = 0;
}
第一類的參數初始化放到了tracker中,下面具體來看各參數的初始化取值:
\left(\begin{array}{ccc} 1&0&0&0\\ 0&1&0&0\end{array}\right)*\left(\begin{array}{cc|c} x\\ y\\ vx\\vy\end{array}\right) = \left(\begin{array}{cc|c} x\\ y\end{array}\right)
x_{t}=\left(\begin{array}{ccc} 1&0&dt&0\\ 0&1&0&dt\\0&0&1&0\\0&0&0&1\end{array}\right)*x_{t-1}
第二類參數的初始化可直接將第一幀傳感器的檢測結果傳入
/* main.cpp中處理部份 */
// 新建一個tracker
tracker tracking;
for(size_t i=0; i<measurement_list.size(); i++)
{
//初始化: 只有當第一次執行時進行
if(i==0)
{
// 將第一幀的數據傳入到tracker所繫結的卡爾曼濾波器中
tracking.kf_filer_.X_ << measurement_list[0].sensor_measurment_[0],measurement_list[0].sensor_measurment_[1],0,0;
tracking.state_.timestamp = measurement_list[0].timestamp_;
continue;
}
// 傳入檢測數據,利用process_measurement函數處理每一幀
tracking.process_measurement(measurement_list[i]);
std::cout <<"X: " <<tracking.kf_filer_.X_.transpose() << std::endl;
//std::cout <<"P: " <<tracking.kf_filer_.P_ << std::endl;
}
(2)predict

如圖5所示,卡爾曼濾波的過程主要由兩部份組成,一個為predict,一個為update:
/* tracker.cpp 中process_measurement */
void tracker::process_measurement(const Measurement &measureTem)
{
// predict
float deltaT = (measureTem.timestamp_ - state_.timestamp) / 1000000.0;
kf_filer_.F_ << 1, 0, deltaT, 0,
0, 1, 0, deltaT,
0, 0, 1, 0,
0, 0, 0, 1;
CalQ(measureTem.timestamp_);
kf_filer_.predict();
state_.timestamp = measureTem.timestamp_;
//update
Eigen::VectorXd z(2);
z << measureTem.sensor_measurment_;
kf_filer_.update(z);
}
其中的predict()和update()為標準的卡爾曼濾波器公式,可單獨抽象在kf這個類中:
/* kf.cpp */
void kf::predict()
{
X_ = F_ * X_;
//std::cout << "Q: " << Q_ << std::endl;
P_ = F_ * P_ * F_.transpose()+Q_;
}
predict中的兩個公式:主要需要進行F矩陣和Q矩陣的計算,F矩陣在(1)中已經進行了解釋,
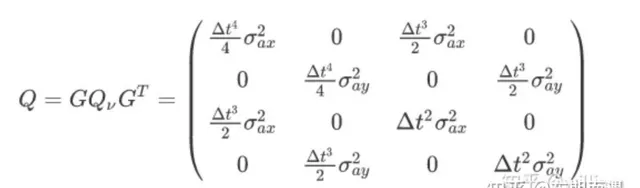
void tracker::CalQ(int64_t timeTem)
{
float deltaT = (timeTem - state_.timestamp) / 1000000.0; //ms to s
float deltaT2 = deltaT * deltaT;
float deltaT3 = deltaT2 * deltaT;
float deltaT4 = deltaT3 * deltaT;
float noise_ax = 3;
float noise_ay = 3;
Eigen::MatrixXd qTem(4, 4);
qTem << deltaT4 * noise_ax / 4.0, 0, deltaT3 * noise_ax / 2.0, 0,
0, deltaT4 * noise_ay / 4.0, 0, deltaT3 * noise_ay / 2.0,
deltaT3 * noise_ax / 2.0, 0, deltaT2 * noise_ax, 0,
0, deltaT3 * noise_ay / 2.0, 0, deltaT * noise_ay;
kf_filer_.Q_ = qTem;
}
(3)update
update的過程比較簡單,直接呼叫標準的卡爾曼濾波公式。
/* kf.cpp */
void kf::update(const Eigen::VectorXd &z)
{
Eigen::VectorXd z_pred = H_ *X_;
Eigen::VectorXd y = z - z_pred;
Eigen::MatrixXd S = H_ * P_* H_.transpose() + R_;
Eigen::MatrixXd K = P_ * H_.transpose() *S.inverse();
//std::cout << "X_ " << X_[0] << std::endl;
X_ = X_ + K * y;
long x_size = X_.size();
Eigen::MatrixXd I = Eigen::MatrixXd::Identity(x_size, x_size);
P_ = (I - K*H_)*P_;
}
4. 結果顯示

同時畫出測量和卡爾曼濾波後的結果,如圖7所示,圖中綠色的點為lidar的原始檢測結果,藍色的線為卡爾曼濾波後輸出的track結果,目標物在做「8字運動」。從圖中可以看出, tracker軌跡的趨勢與lidar檢測的結果基本一致,且經過卡爾曼濾波後,藍色track的軌跡相對綠色的原始檢測點更加平滑,體現出了卡爾曼濾波器的作用。
/*
draw
.
py
*/
import
matplotlib.pyplot
as
plt
import
numpy
as
np
x
=
[]
y
=
[]
detectX
=
[]
detectY
=
[]
# 存放結果的路徑
with
open
(
"jieguo/test7.txt"
,
"r"
)
as
f
:
for
line
in
f
.
readlines
():
line
=
line
.
strip
(
'
\n
'
)
data
=
line
.
split
(
' '
)
count
=
0
for
s
in
data
:
if
s
!=
'X:'
and
s
!=
''
and
count
<
2
:
if
(
count
==
0
):
x
.
append
(
float
(
s
))
count
+=
1
continue
if
(
count
==
1
):
y
.
append
(
float
(
s
))
count
+=
1
# 存放原始檢測結果的路徑
with
open
(
"./obj_pose-laser-radar-synthetic-input.txt"
,
"r"
)
as
fileIn
:
count
=
0
for
line
in
fileIn
.
readlines
():
line
=
line
.
strip
(
'n'
)
data
=
line
.
split
(
'
\t
'
)
if
(
data
[
0
]
==
'L'
and
count
<=
9
):
detectX
.
append
(
float
(
data
[
1
]))
detectY
.
append
(
float
(
data
[
2
]))
#count += 1
print
(
detectX
)
print
(
detectY
)
plt
.
figure
(
figsize
=
(
6
,
3
))
plt
.
plot
(
x
,
y
,
'b'
)
plt
.
scatter
(
detectX
,
detectY
,
s
=
10
,
color
=
"g"
)
plt
.
show
(
)
參數討論
(1) 調整P矩陣初值
將P由原來的 \left(\begin{array}{ccc} 1&0&0&0\\ 0&1&0&0\\ 0&0&1000&0\\ 0&0&0&1000\end{array}\right) 調整為 \left(\begin{array}{ccc} 1000&0&0&0\\ 0&1000&0&0\\ 0&0&1000&0\\ 0&0&0&1000\end{array}\right)

從圖8中可以看出,調整P的初值對結果無影響。因為從理論上講,P的初值只代表了剛開始時我們對目標物狀態量的一個置信度,將x和y的置信度從1調整為1000, 說明我們對剛開始時目標物的位置不太確定,是隨便估計的。但是隨著測量結果的叠代,目標物狀態的置信度會逐漸回歸,而不受初值的影響;
(2) 調整R矩陣
將R矩陣由 \left(\begin{array}{ccc} 2&0\\ 0&2\\ \end{array}\right) 調整為 \left(\begin{array}{ccc} 0.02&0\\ 0&0.02\\ \end{array}\right)

從圖9可以看出,調整R矩陣後,卡爾曼濾波輸出的結果更加貼近傳感器的檢測結果,但平滑度降低。從理論上分析,R矩陣表征的是傳感器測量的誤差,當我們把R矩陣對角線元素由2調整為0.02時,其物理含義為,原來傳感器的測量誤差為2,調整後的傳感器測量誤差為0.02,測量誤差減小了100倍,且誤差只有0.02,表示我們十分相信傳感器的結果,這樣勢必會導致卡爾曼濾波的結果更加貼近傳感器原始的檢測結果,理論與實踐表象一致。
(3) 調整Q矩陣
Q矩陣中 noise_ax = 3; noise_ay = 3 調整為noise_ax = 0.03; noise_ay = 0.03
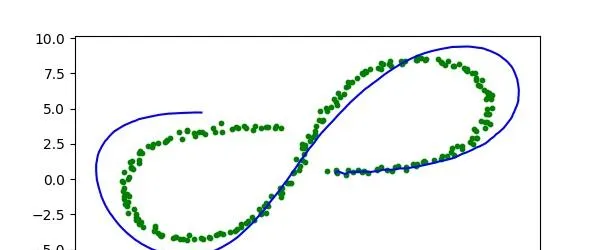
從圖10中可以看出, tracker的估計更加平滑,但是偏離原始傳感器檢測結果也更遠了。Q矩陣表征了偏離運動模型的雜訊的大小,當我們將雜訊 noise_ax 和noise_ay 從3變為0.03時,實際上是降低了過程雜訊,也就是更加相信我們建立的運動模型(F),也就是相對不太相信傳感器檢測的結果,這就會造成我們偏離原始檢測結果。
以上是本文的全部內容:。
程式碼及數據連結: https:// pan.baidu.com/s/1dwYxjJ HLoK_Ox5KcRHgY5A 提取碼: 7h8r
參考
- ^ 數據集來源: http://www.udacity.com
- ^ Q矩陣的推導方式舉例 https://mp.weixin.qq.com/s?__biz=MzI1ODYwOTkzNg==&mid=2247508342&idx=2&sn=a701c65ed5b5f92f6342ec33b2ea3c8c&chksm=ea076709dd70ee1f3fe318ee446649173a33f7dd2e28f9804c39e343f20de5bccd82f453fb25&mpshare=1&scene=1&srcid=0220DoPOR0CZDTKVgvobFDRL&sharer_sharetime=1613783463771&sharer_shareid=def5d1aee922d88fa623ca1b2829e1b1&exportkey=AzSVmNVaVNURmrtGbLbGqls=&pass_ticket=iyHntop8n5h0fEKwEtMpyGNmmY8acj76sGVADlrFzXB+xvPwOQXHalukuVgreDj&wx_header=0#rd











