最近要考试了,就不继续往下看,开始一边复习考试一边稍微看看最近学的机器学习相关。
这一篇想说的是EM算法。想说的原因是在回顾PRML第三章最后关于超参数的evidence的求解过程时候突然感觉这和EM似乎有点像。这是evidence的优化目标:
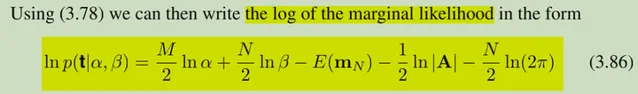
而这个evidence的产生是来自于这个分解(marginalization):

其实fully bayesian的视角就可以看成是对整个模型加了个隐变量,因此似乎理论上也可以用EM algorithm那套对于隐变量模型的迭代逼近参数算法来搞,但事实上并没有这么用,为什么咧?
我的理解是:它「用了」,也没有「用」。
前半句的原因是来源于第二张图,它和对于EM algorithm模型一样,尝试用marginalization的方法对原来的概率进行分解(EM algorithm据我所知有两个proof,分别使用两种不同的分解,一个采用jenson不等式,一个采用kl divergence来证明的,这里说的是关于jenson不等式的那个proof)。
后半句是因为,这个model和一些用em algorithm的model还是有些不同之处的:那些model(比如GMM)积分号里面虽然能够解析的写出来,但往往不能直接写成一整个distribution的形式;而这里的经过一些化简,就是一个gauss distribution。因此从某种意义上来说,此处的问题复杂度更低一些,可以用一些更「合适」的迭代算法(不至于在这一步就直接用不等式放缩),继续的进行一些对于目标化简在开始我们的approximation process,而我们的目标化简过程就是从第二张图化简到了第一张图。这就是普遍的EM过不来的一步。
然后现在的问题就是转化成了对第一张图的式子做近似,因为此时我们又遇到了和当初在考虑EM算法时相似的问题,直接求gradient是不解析的,再通过观察这个式子,我再贴一遍:
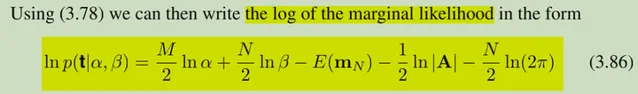
它的第三项是关于alpha比较复杂的,其他部分关于alpha的gradient都是形式很好的,那么那么迭代的灵感就来了,根据初值alpha得到第三项,然后再对固定第三项后的式子求gradient,这样就可以得到一个迭代的方法了。这也就是PRML在处理这个问题给出的一个具体方法。( 更新:这种灵感也在ADMM算法中利用过。对于non-smooth的部分采用Proximal Operator的闭式解;对于smooth的部分采用正常的优化思路 )
再来回顾一下EM算法:为了形成对比,采取同样形式对目标进行拆分(marginalization形式的拆分,但拆分之后不做分解),EM的思路要复杂许多(构造性强很多),它把目标转化成了一个期望,再利用凹凸性得到一个ELBO(可达下界还是啥名字来着),因为这种构造方式我们可以得到这种approximation的一些很好的性质(收敛性,和一些几何意义),甚至利用这种分解还能推广到广义EM算法(GEM)。其实EM算法的本质也是一种坐标下降法,只不过EM算法的第一步比较漂亮是因为某些形式比较好的优化函数可以得到解析的第一步(E步)的分布;而GEM算法就是建立在一些形式不太好的优化函数不能直接得到解析的第一步(E步)的分布,因而转化为另外一个对ELBO的argmax问题,因此EM算法也可看成是MM算法(对于ELBO两个分量利用坐标下降法轮流进行argmax的迭代算法)。
值得一提的是,EM算法找到的ELBO是一个有一定好的性质的量,因此用ELBO近似原本的优化目标,会产生一个可解析(某些模型,如HMM,GMM)的迭代方程。(如果这个近似的目标比原来目标更难求,那显然这个方法是不可取的)
具体公式可参见白板视频(我是想总结一些除了公式外的思路)
最后来总结一下,这两个算法本质其实都是一样的,利用一些分解来构造可迭代的逼近序列,只不过EM算法的构造更加精细(相对),泛化能力较强,效果也很好;但遇到具体问题,更应该先努力拆分化简优化目标,如果形式很差的话再考虑EM\GEM算法,不然可能会有一些更简单、效果也不错的迭代方法(比如PRML对于超参数的evidence的求解)。











