● 泰勒公式是在局部,用一个多项式函数,近似地替代,一个复杂函数。这一点,大家多多少少都是了解的。下面我想说明,为什么多项式函数可以近似替代复杂函数,以及泰勒公式展开的本质是什么。
为了方便大家理解,我只用最简单的「带佩亚诺余项的麦克劳林公式」做范例。看完回答后,请大家务必参照本文思路,再亲自对一般的泰勒公式进行分析,你就能彻彻底底地理解泰勒公式。
● 一般教科书把麦克劳林公式写成以下形式:
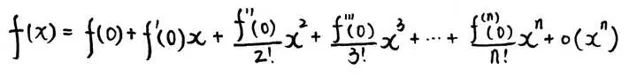
初学者一看就懵了,这啥呀这是,只能死记硬背,觉得这个公式很不可爱。
但是,如果偷偷把展开式中的【阶乘】换个位置,譬如这样:
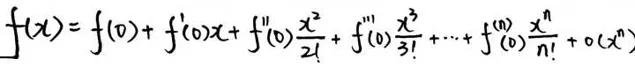
这个公式瞬间就变得和我一样可爱。书本上的公式,仅仅是为了方便求各阶幂函数前的系数;而调整阶乘位置后的这个公示,才真正触碰到了泰勒公式美丽的灵魂。
● 大家仔细想想,在泰勒展开式中,每一个幂函数(x²、x³…xⁿ)和与其搭配的阶乘(2!、3!...n!)有什么联系。
大概没想出来,但是如果我告诉你xⁿ的第n阶导数是n!呢?
也就是说,x²的2阶导数是2!,x³的3阶导数是3!,这样你能看出什么吗?
是的,你会发现,在x=0这一点,对泰勒展开式(多项式函数)求3阶导数值,其结果为f'''(0)。
因为f(0)、f'(0)x、f''(0)x²/2,分别在1次求导、2次求导和3次求导中,求导成了0;
而之后的456更高阶幂函数,在计算导数值时,需要代入x=0,其结果全部为0;
x³的3阶导数是3!,和分母的3!约去,只剩下了f'''(0)这一项。
——多项式函数(泰勒展开式)的3阶导数值,就是复杂函数f(x)的3阶导数值。
同理,多项式函数的4阶导数值,就是f(x)的 4阶导数值;多项式函数的10086阶导数值,就是f(x)的10086阶导数值。
● 大家或许有那么一点感觉了,为啥泰勒展开式都是由幂函数组成。
这并非某些答案所说的「因为幂函数很简单」,而是因为幂函数(x³)一旦与相应的阶乘(3!)组合,就可以在对应阶数(3阶)求导后【消失】,只留下这一阶的导数值(f'''(0))。
在这种意义上,泰勒展开并不是唯一的,因为任何在对应阶求导后能够消失,并只留下导数值的函数,都可以作为泰勒展开的备胎。可惜的是,幂函数与阶乘的组合,是我们已知的唯一具有上述性质的函数,因此,这种唯一性决定了泰勒展开能够且仅能够由幂函数表示。
● 总结:泰勒公式的灵魂是导数值,而非幂函数。在展开的这一点,泰勒展开式与复杂函数f(x)的每一阶导数值都完全相等。而这种「各阶导数值相等」,揭示了多项式函数和它想要替代的复杂函数f(x)在「每一个维度上完全相同」的奇妙的事实。
● 打个不精确的比方,在【某一时刻】,有一个法外狂徒张三(复杂函数f(x)),想让李四(泰勒展开式)替代自己去上学。
在这一时刻,李四和张三的外貌相同(函数值相同),体型相同(1阶导数值相同),声音相同(2阶导数值相同),那我们就可以认为,或许在这一刻,让李四替代张三是比较合理的。如果在更深入的维度上,他们具有相同的智商(3阶导数值相同),具有相同的记忆(4阶导数值相同),那么用李四替代张三就更合理了。如果他们具有相同的喜恶(5阶导数值相同),具有相同的三观(6阶导数值相同),那么用李四替代张三就越来越合理了。
这也是为什么泰勒公式展开越多项,在展开这一点的附近,就越接近f(x)本身。
● 现在再看一眼公式,大家能【理所当然】地理解为啥泰勒公式能够如此展开了吗?
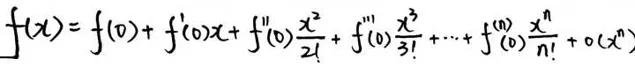
你在写出展开式的时候,内心活动应该如下:
在x=0这一点,
① 他们的函数值相同,所以写出第一项f(0)
② 他们的1阶导数值相同,所以写下f'(0),要求求1阶导的结果为f'(0),那么后面得添上x
③ 他们的2阶导数值相同,所以写下f''(0),要求求2阶导的结果为f''(0),那么后面得添上x²/2!
④ 他们的3阶导数值相同,所以写下f'''(0),要求求3阶导的结果为f'''(0),那么后面得添上x³/3!
……
⑤ 他们的n阶导数值相同,所以写下fⁿ(0);要求求n阶导的结果为fⁿ(0),那么后面得添上xⁿ/n!
——如果你能理解当中的本质,这是一个简单到不需要记忆的公式对吧?
● 希望你们看完这个回答后能够体会到,f(x)泰勒展开成怎样的函数并不重要,重要的是,在进行了某阶求导后,这个函数一切外在的躯壳都随风而逝,只留下了在这个维度上和f(x)完全相同的事实。










