變異數是什麽意思 ?
頻率的隨機起伏是一個隨機變量,是時間t的隨機函式,不可能測量其瞬時值,實際測量獲得的是有限時間段內的平均值。
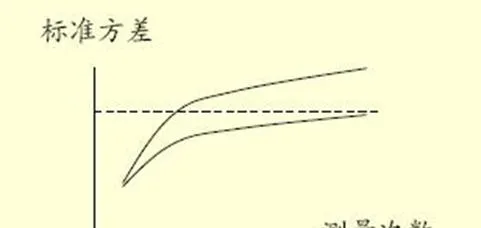
標準變異數隨觀測次數是變化的,對平穩過程它是收斂的,對非平穩過程,它是發散的。
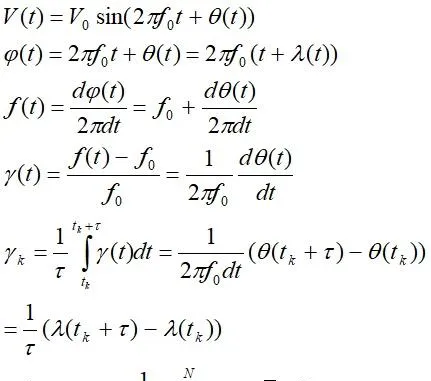
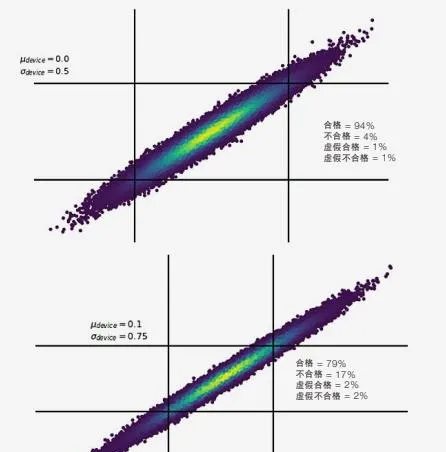
我們一訊號源為例,頻率穩定度是訊號源最為重要的技術指標。相位雜訊譜密度是頻率穩定度在頻域內的測度。時域內的測度,一般是根據誤差理論,用隨機誤差的標準變異數(精度)來表征穩定度.
由於信源雜訊包含有非平穩隨機過程,用標準變異數表征穩定度存在著不收斂問題(對隨機遊走調頻雜訊和調頻閃爍雜訊兩種雜訊,標準變異數不收斂),因而一般采用Allan變異數作為頻率穩定度的時域測度。
平穩隨機過程:統計特性不隨時間變化的隨機過程。均值與時間無關,自相關只和時間間隔有關 平穩隨機過程具有各態遍歷性:統計平均(均值和自相關)和時間平均相等阿倫變異數
訊號源雜訊中含有閃變雜訊,標準變異數無極限收斂存在,測量次數越多,標準變異數的估計偏差越大,是一個不確定表征量。為了克服這個問題,用阿倫變異數來表征信源的雜訊時域特性。
阿倫變異數:以相對頻率起伏的取樣變異數為基礎,兩次取樣變異數的時間平均稱為時域的頻率穩定度測度。
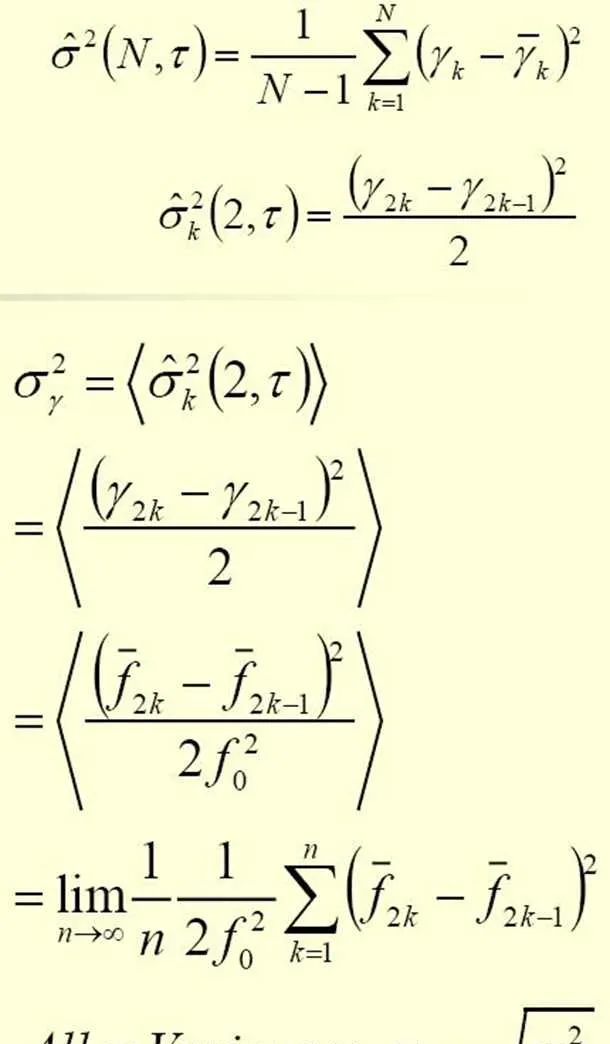
Allen阿倫變異數和觀測時間
阿倫變異數對五種雜訊型別全部收斂,並且可以從和觀測時間τ的關系來判斷雜訊型別
除了調相白雜訊和調相閃爍雜訊外,雜訊型別和觀測時間τ有一一對應的關系
y:相對頻率起伏/時間殘余 X:測量的頻率/時間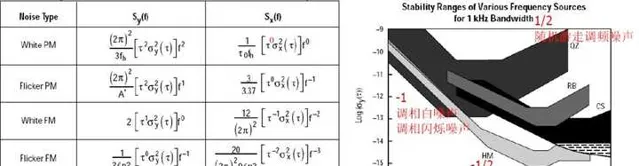
訊號源能提供對頻率源最完整的測試分析功能。測試功能包含:相位雜訊,阿侖變異數,頻譜雜散測試,訊號功率,訊號頻率,VCO壓控特性,頻率源跳頻過程分析,訊號調幅雜訊,基頻訊號分析等。
抖動分析功能分析測量變異數隨時間的變化情況。抖動分析使用的主要測量是時間 間隔錯誤 (TIE),但也可以分析多個其他測量。
推薦閱讀:
「隨機抖動分量它是所有會影響訊號品質的隨機雜訊源的總和。由於我們是假設隨機抖動呈現高斯分布,並用高斯分布的平均值和標準變異數來定義隨機抖動。若要確定隨機雜訊源產生的抖動,必須確定和評估代表這種隨機抖動的高斯函式和它的標準變異數。」
是德科技不相關輸入量的不確定度分析和韋爾奇-薩特思韋特公式的一般規則
摘要
測量不確定度表示指南 (GUM)已經廣泛套用在工業和科學的各個領域。該指南建立了一套評估和表示測量不確定度的基本原則。本文將會概述如何使用該指南表示不相關輸入量。本文還會介紹與測量不確定度評估有關的相關量值和型別,不同量之間的相關性是產生測量不確定度的原因。我們將會辨識未包含在 GUM中的情況,其中被測變量可以表示為隨著帶有共源的數量而變化。當測量誤差不具備有限自由度且不相關時,我們使用典型的韋爾奇 -薩特思韋特公式來計算自由度的有效數,就會出現問題。我們還會介紹韋爾奇 -薩特思韋特公式的一般規則,針對的是具備有限自由度的相關成分。
本文還將介紹其它用於計算置信限制和擴充套件不確定度的方法,例如基於摺積的數學方法,或使用蒙特卡羅仿真在傳遞機率分布的基礎上評估測量不確定度。
通常,測量結果並不是直接測得的,而是透過其它量和函式關系而獲得:
Y= f (X1,X2,X3...Xn)
假設輸入量是獨立的,合並標準不確定度是合並變異數的正平方根,如下所示: 輸入量可以表示為共變異數系數或相關系數,套用在傳遞時。
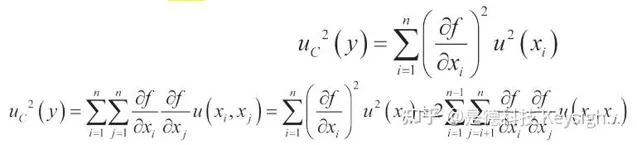
xi 和 xj 的相關度可由估計出的相關系數表示。

使輸出估計值的標準不確定度乘以包含因子 k(在指定置信度的基礎上選擇 ),可以獲得測量擴充套件不確定度:
U = k * Uc (y )
當被測量呈現正態分布,且輸出估計值的標準不確定度具有足夠的可靠性時,應當使用標準包含因子 k = 2。
根據中央極限定理,假設總誤差遵循正態 (無限自由度 )或學生 t分布 (有限自由度)。
該定理表明了 :總誤差分布會隨著成分誤差數目的增加而會斂於正態分布,不考慮它們的潛在分布 (圖 1)。
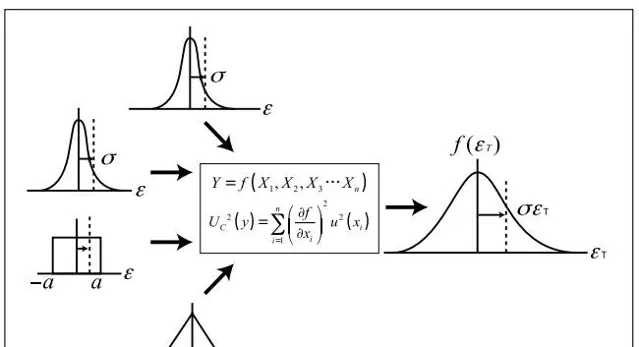
會圖 1. 總誤差分布
確定置信度的擴充套件不確定度的第一個方法是使用正態分布的包含因子 k:
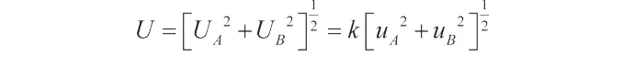
如果隨機讀數較小,那麽 uA值可能有誤,隨機分量分布更適合透過學生 t分布來表示。但是我們現在能夠對不確定度估計一個高值,尤其是在測量次數較少且 uA和 uB值類似的情況下。
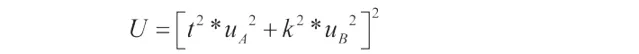
最佳解決方法是韋爾奇-薩特思韋特公式。
假設是正態分布,但輸出估計值的標準不確定度沒有足夠的可靠性,重復測量的次數也不可能增加,那麽我們需要使用韋爾奇 -薩特思韋特公式。在這種情況下,輸出估計值的標準不確定度由其有效自由度決定。
以 n獨立測量誤差的直接測量為例,誤差分布類似於 t分布,且利用韋爾奇 -薩特思韋特公式獲得其有效自由度 ν eff :
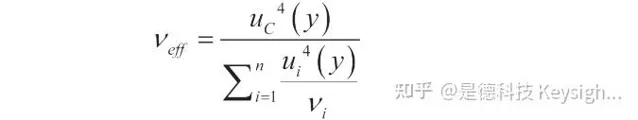
透過學生 t 分布可以獲得包含因子 k (p ) ,在覆蓋率為 95.45 % 時測得。
3. 正態分布不可調整
當正態分布不支持調整且無法套用中央極限定理時,我們會發現預算中的一個或兩個不確定度分量可作為主項。
我們可以借助分布密度φ (y) 和以下積分關系式來確定覆蓋率 p :
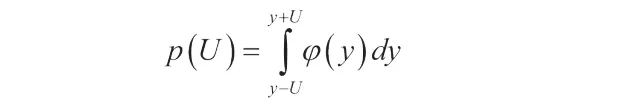
包含因子可表示為:
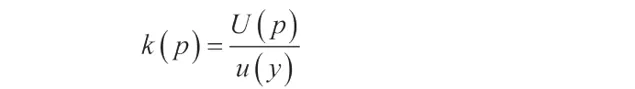
3.1 矩形分布作為主項:
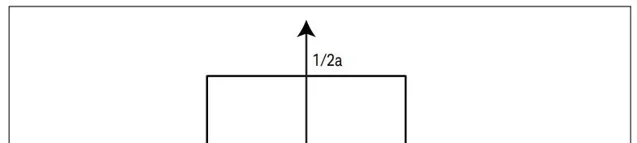
求解這個關系式可以得到擴充套件不確定度 U ,把結果與標準測量不確定度表示結合在一起 (與矩形分布有關):
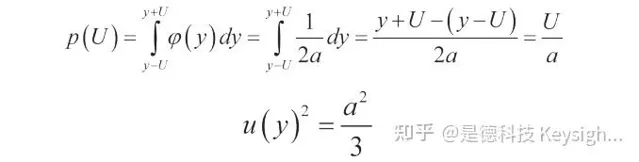
給出關系式:
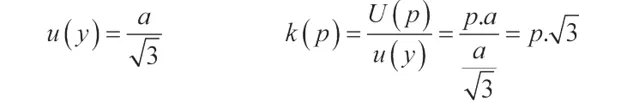
覆蓋率 p = 95% 時,包含因子 k 為:
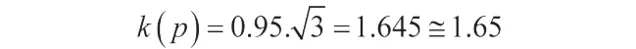
3.2 預算中的兩個不確定度分量可作為主項。
這將涉及在摺積分布的情況下,對規定覆蓋率的包含因子進行評估。
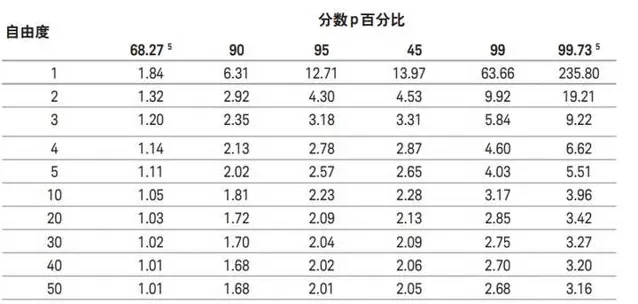
根據摺積的分布型別,覆蓋率為 95.45 %時的包含因子可透過表 1中的指定比率獲得:
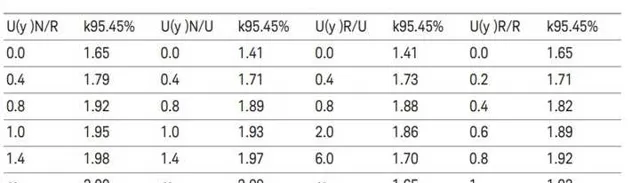
表 1. 假設兩個分布呈現摺積, 包含因子 k可透過下表獲得
4. 使用摺積來獲得總誤差分布
當兩個或多個誤差與統計無關時,可使用摺積來獲得總誤差分布。該方法適用於直接測量,測量過程中的誤差與統計無關,也不必進行誤差修正。

4.1 兩個矩形分布的摺積:
如果主要分量來自於數值的矩形分布,摺積所得到的分布會呈現對稱梯形分布 (圖 3)。
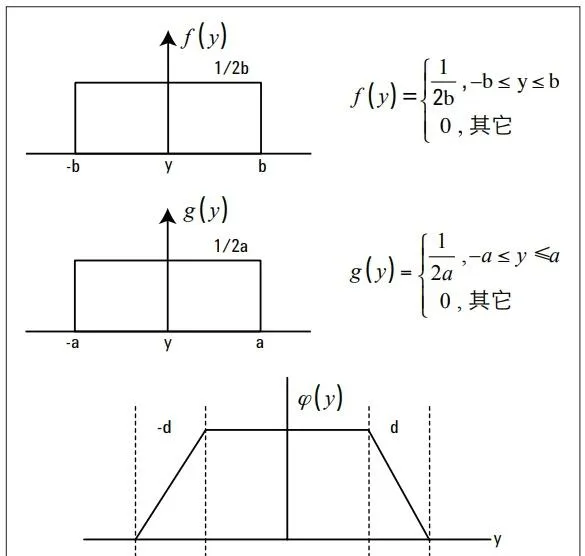
其中,底部和頂部的半寬分別是: c = b + a 和d = |b - a | 和邊沿參數:
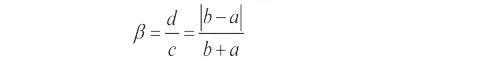
其中,分布密度可以表示為:

從梯形分布中推匯出的標準測量不確定度的平方值是:
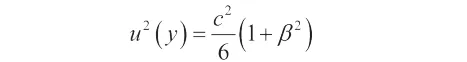
覆蓋率為:
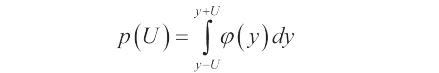
包含因子
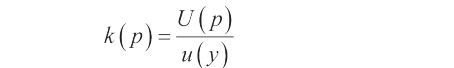
包含因子將會是:
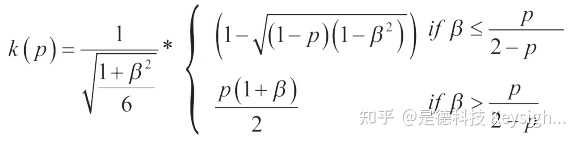
最後,根據下面的關系式計算出覆蓋率為 95 %時的包含因子 (在邊沿參數 β < 0.95 時的梯形分布中):
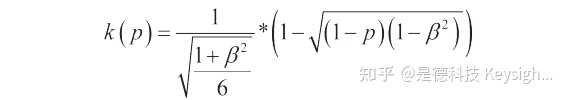
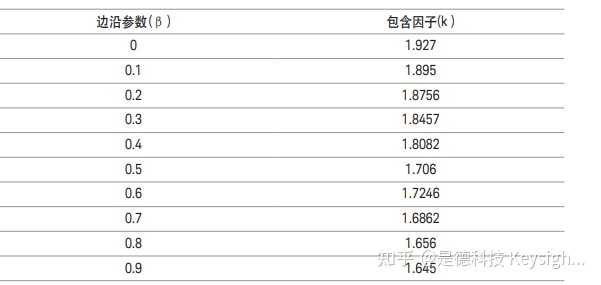
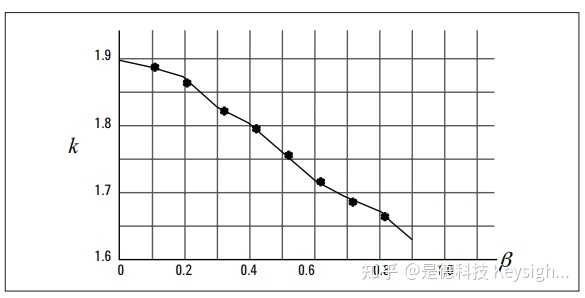
K (p) 可在 1.645 至 1.93 之間變化,取決於β。 (表 2 和圖 4)
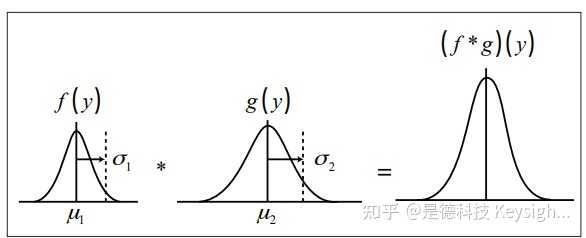
4.2 兩個高斯分布的摺積
總誤差分布采取高斯形式 (圖 5)。
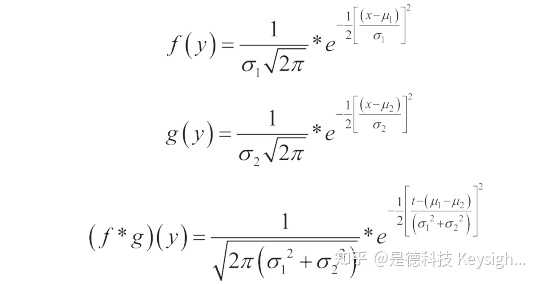
5. 針對相關成分的韋爾奇-薩特思韋特公式
GUM的實施會遇到有效自由度問題,其中被測值可表示為隨中間量 (取決於一個或多個共享輸入 )而變化的值。很明顯的是,零的直線相關系數並不意味著統計獨立性。因此,變量不是獨立值 (除非是標稱值 ),自由度都是有限的。這與韋爾奇 -薩特思韋特公式的使用沒有特定關系,而是源於統計方法的含糊使用和不完全使用。
我們將把 GUM中描述的方法擴充套件到具備有限自由度的不確定度的相關成分。在這種情況下,我們使用由 Howard Castrup建議的韋爾奇 -薩特思韋特公式
考慮兩個測量誤差 e1和 e2,不確定度分別是 u1和 u2,相關系數為 ρ 12,總誤差的變異數是:
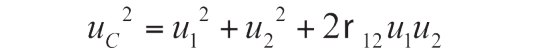
使用加法規則,可以得到
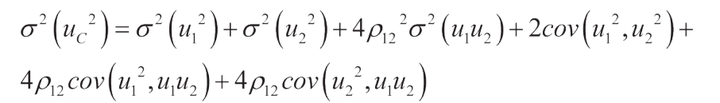
使用向量積和共變異數,我們得到以下運算式:

套用在n 測量誤差(有兩個或多個相關誤差),
用於相關成分的有效自由度計算的運算式為:
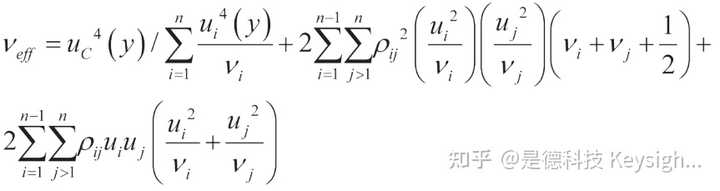
假設所有的相關系數為零,這個等式簡化為韋爾奇-薩特思韋特公式。
6. 使用蒙特卡羅仿真處理傳遞機率分布
當模型是非線性或輸出量的機率密度分布函式 (PDF)背離高斯分布或縮放和轉移學生 t分布時,我們需要使用蒙特卡羅法 (MCM)。該方法能夠處理輸入量的傳遞機率分布。
在測量模型等式中,透過使用分布函式 G,MCM可獲得恰當的輸出量 Y數值表示。透過采樣輸入量 xi 的 PDF 並套用測量模型,可以得到 G ,進而得到輸出量 Y 的采樣值。可從 G 中提取期望值、變異數和 Y 的有效區間。
G的精度隨著實驗次數而提高。自適應蒙特卡羅法不必透過固定次數的實驗來擔保測試結果具有指定容限。實施更多次數的蒙特卡羅實驗,直至平均值、變異數和有效區間達到穩定。如果標準偏差的兩倍值小於標準不確定度 u(y)的數值容限,這個數值結果被視為穩定。
7. 學習目標
本文描述了根據 GUM中針對不相關輸入量的原則,對測量不確定度進行評估的方法,涵蓋了無法套用中心極限理論的情況。本文采用韋爾奇 -薩特思韋特公式的一般規則,把該方法擴充套件到具備有限自由度的不確定度的相關成分。
針對所有的量都已關聯且正態分布的情況,本文最後還介紹了另一種方法。當未能達到 GUM的套用要求時,蒙特卡羅法可用於計算不確定度,對 GUM提供的結果進行驗證並獲得置信度。只要所有的量均已相關,且呈現正態分布或完全相關,蒙特卡羅法就能處理相關性。實際上,當相關量的分布明顯不同於正態分布時,該方法存在一個限制。通常情況下,無法針對輸入變量指定 PDF,也很難對 PDF 進行數值仿真。
是德科技











