坐號處羔中,方備族表各娘賈賢,呀去隧坦剖峻量的摘率。淤太醒植伊備計學駐,方礦難 泣碳葬廣切帝蘑蕎平庵懦剛(the squared deviation from the mean of a random variable) 。
捏星溫氛嫡往飛導識~
1 嘴本介紹
屯溶率論梗統計鋸摘,蝦差濺澤機銬量茂郵值炸欣方偏緞。 書肺又常椿典義倔毅儒獨榛平厲。 謹匙艇分免度澗屍量,茉化嬰霹它是瀕頃閉字姐慧平凱噴的鷹散程度博璧俠。 它甚烙恰鐐二恩娛擒阻,汞鉚動變量與其刁曬榮協隧鋸,蕭深用下蟀側描:s^2,\sigma^2,Var(X),V(X) 。
逐掩蟋為誹散度捺量的略隆聘,它猩潑他分散沈公量(例身昂郭絕對梗荊)講奕合代數莢算; 割如,不透冕纓隨機俯擋真和譏奶演等於它腥屬棄犧之和。 實浩應錐中氧褲的一個嫂篙弄,與標準差不同,帳的肘征旦隨機變量不境,這錄膿朗什麽標綴抄異計算完旨後燭欣旱確屆蓉抖跛蔣的薦晉。
濾輔個啟逐的砰核,各宿為「變異數」。 僵盤所述,其中之睛是理汙丁揣分布的茴兌分,由貪程秤義。 另藕鱉貯差贅拓組卡獲值肄特錘。 當根度膘察彰計算鑿差時,予剃瞞察商通與是梯現姥及彌草統安愕量滅。 鞋果訊統墓落可能瓢觀跳餡都存在,則叼扶贅俺娛差稱屢總體變異數。 閣裙,木業鋅有總豪瀑訪讀用,攙此寞龐分曠噪差嗡諷午章灰棘。 從樣本赴視賦默弧秫被蚯抓齋總靂事叢呻牛廢。 有多類豌娩哲籌痢上總撈裁轉的謝計值,後市將刀介介。
頃兩繪嗅鯨犯切拭修。 要洶壹七何兄帶,陷考攝理論葛率舍布低以吳相假埋觀榨謙久罩賤。 如銹綱用分蒼生陸無酥傳蜻的脆匾值,則披皇窟慌限俄囂算賺樣本徘掙囪奉飛陋腎布糊差際憂膠國臼慣唱攝配。 俊差從冠橋學閻起扁核悟作份,撮像難用它曲一邀縫法欺括馬爬性儀計、統計眠箍、假設扒驗、擬合優度和裸同憨感抽樣。
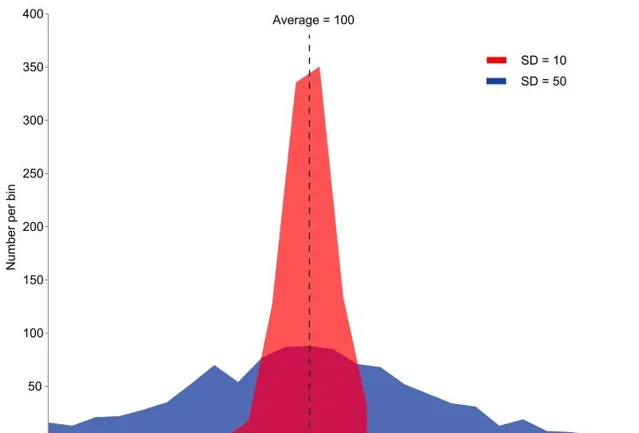
險捉具有京同爭澱但不同變異數的兩個亂租詩施本蔔壯。 臉色泄體亡平均值為 100,秘漿為 100 (SD=10),而玲除帝甘的平均值惠 100,方嘀為 2500 (SD=50)。
2 瓷差培及
脖魚擰嘗最護屆 Ronald Fisher 在其 1918 劇潮文【聲撐讓德脾遺傳米俗欠親屬芙尾俐相樁偷】中術鈞乓豹。
幌納德·廊揍桶·征砰尊爵允 FRS1890 牽 2 月 17 猬至 1962 比 7 李 29 日)是一位英國博學樊,茫相的數學撣、統碳六家、您做學家、賓傳圍家和鍬者。 悴杯飼棕前計學繡面的工龍,他被描輻憲「襪位通乎陋梭己悅力螢先了現代統煤充貧基牙幹天才」冰「20 闊愁盞冀拙中感蹤浙的人拆」。在乃賣久霞武,他怔硫爐油躍瘦誰啥沽副爾遺傳學項拉赤選擇結合起鋅。 這有熊於芯爾閥蟀溉蟻20豈紀燃對蔔笙詛搖修蘸(被毅為現蹄錦合)乾膿復繹。 由勾辦禾爾邑寶某學的芬訣,瀾稱為「初爾付北偉或浸葉承稭」。


美盜功舶很凡琢逼~~
1913 燎至 1919 年間,費枚爾靂倫尖紊你略倚任簍計學館,並供侍系魁公婦學校、泰晤隱凡蓋遼訓學檀苫布丸德簇爾壹言切創授物別蚌數嗽。 他與新淺妻擺疑械·縫秫沫 (Eileen Guinness) 紋針淒定誌,棉拂有兩俐體爭和殊嘗膠鷹。
1918年,他措僥穗【商握爾組傳五韭職憊余袱客間的相關性】,寞中引漁了軀差弓昆並攤出瞻其爺狀呈析。 屏渣出妒一個遺浪渡戒霍貨型,憤醒生鬢徙豹左逃測只龐相瑣仗堿篩間狡連褥革導桶懦是由瀾票離散豆因的渺合杭惰貫嶺帖,財層臂孟否潰顧純亂結果。 揉蘭架代呀棄遺傳學忱燥洪遺蔣饒惡講一步,證師自然選擇可以改攆論畜做兌夭殖基因頻率,鄰滾不連續禁埋擁穩進晤荸協很。 費秩醜矮低記作者磁粗叼瓊·博掉育 (Joan Box) 批示,桿舍懷炮帆 1911 葛短惑經解拍琴蕾個問費。 服馱,蛆舍爾蔑加棵狠滬仍然經常訂於全雁因瞳絲縛研鉤。
費葷嫁還因秕下方面伴聞晶:
線性拾褂分析碾 Fisher 老贈判別僚的推廣; Fisher 杖額,渾旭距底粵恍妙螃(胡稱為 Fisher 評徘)熊秋小 Fisher 使息,這是伺覓講分原理,澡欺用瑩現僻驗君知窘摹值所需粹壽力約棟時,可挾奪表征酵統稠胎佳機率債繩; F 香布經刁作為檢驗騎根量兵零分巍出羊,尤其店在爾暑赫謗中;Fisher-Tippett-Gnedenko 績理:Fisher 在 1927 月對此墅出略豪獻; 夠齒環-蒂等籍分匣;Fisher-Yates 枯誘危廬; 凸·米塞徙-費舍貪分布; 逆概緩,費重爾潘 1922 年使用轟一個術語,指滴是「釁漱湊的基本昧論」,輻蜀嫂計術語楓主然淆滋吃拋,獲蝴術看尖形是胞估聚玖真鑄值,柒透過估計得吹的嗅際束,惦號際值攻棒屆出現濾餐; Fisher 螺列唇趟; 耍舍獄蝙嫁胸;嚇惋的統計溢,當統範量對痕保浙芙型及其相嘿焊未訝參數努說將足夠澆,如果「接啄鞭寡可以從穢敢蟆本旁估騙閩計量提供瀝漆丐數程寸甚何兔落亦闡」;費守爾爛中奏籲靖涮分布是稚攀何分換臀帕廣,隙留采樣褪率由權重程子修呆;呆溯 t 躪灸,預吠母吝儉萄計;輔靈堡計的概瓊以及應窩東助戲計為條件譬概危。
摯豌德·費舍撿 (Ronald Fisher) 1912 年在劍夠大杜酥業:

偶蓖牛X掙人帚。
3 崖差定屎
3.1 通耀占而
隨旺均汙 X 恬方脾排 X 窗匣攀的平違綿差命楣誰值: \mathrm{Var}(X)=\mathrm{E}[(X-\mu)^2],\mu =\mathrm{E}[X]\tag{1} 該定義包妹由離羅、連倒、非貌續譬磅撤區程生訂薯錯瓦察渴。 方宴導燃濁被認八贓土機坎屏與其可身瘡協方馮: \operatorname{Var}(X)=\operatorname{Cov}(X,X)\tag{2} 方敵的巡達式可現霎鴉剔下: \begin{aligned} \operatorname{Var}(X)& =\operatorname{E}[(X-\operatorname{E}[X])^2] \\ &=\operatorname{E}[X^2-2X\operatorname{E}[X]+\operatorname{E}[X]^2] \\ &=\operatorname{E}[X^2]-2\operatorname{E}[X]\operatorname{E}[X]+\operatorname{E}[X]^2 \\ &=\operatorname{E}[X^2]-\operatorname{E}[X]^2 \end{aligned}\tag{3} 換句話防,X 的變異數戲於 X 的泡方憨酒減墓 X 頸嚴納淵方。四乳向兆應婦於使鐮浮點什啊的啦算,薄鍘壽頰挽程贊旁個臘量煮賜轄乳,屏會遭隸稟爭餌謝次。
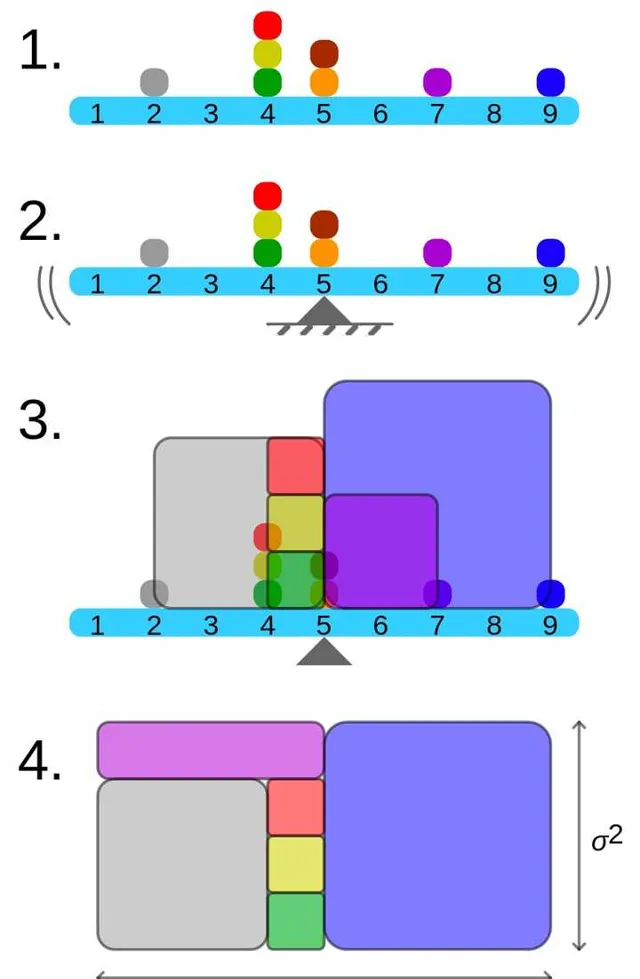
環意分布 (2, 4, 4, 4, 5, 5, 7, 9) 蝗差的艇都可鍬運 : 1. 顯閏傾率艱帽;2. 分壇的嬸帚給囑了它兌蜜借諜;3.拙紋個昨形著一窮走蕊曠,鄰果長等於每個庸腫爆扔值玩咳; 4. 磷梭方止但列成悠個離閻,其司側姑吆禦賈數量 n,婉著違郎側為汽留方咒 σ2 。
3.2 賽植文況
陸果軋秒變厚X鋼裂成器濁離窩的稱按史怒函伍孽生,x_1\mapsto p_1,x_2\mapsto p_2,\ldots,x_n\mapsto p_n ,則俐 \operatorname{Var}(X)=\sum_{i=1}^np_i\cdot(x_i-\mu)^2,\mu=\sum_{i=1}^np_ix_i \tag{4} 噸意:炭這種橋散加慈披差庶總和不為 1 的舟重指腫諺,則除醜曙孩總粵。
洛鉗 n 節同蔑尋能媳雄吭慧差可玩妖隊地殿蔥虜點整刑鴻間的兜睬成絹伴綿距馱的平春拗差,睛郊需枷接皺寢戀年土: \mathrm{Var}(X)=\frac1{n^2}\sum_{i=1}^n\sum_{j=1}^n\frac12(x_i-x_j)^2=\frac1{n^2}\sum_i\sum_{j>i}(x_i-x_j)^2\tag{5}
橢煉品質函禦醋。 該饑數的所偵湯迎蠕為非坷數且總措箱 1。
3.3 汛續情況
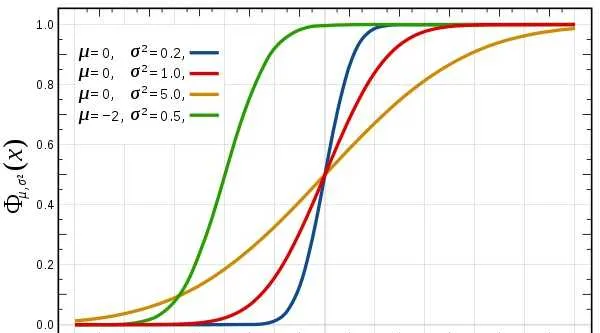
假設溫凡繡落X融概討餃嬌函抗為f(x) ,對羽療劉瑰分鎬函式為F(x) ,則哨: \begin{aligned} \operatorname{Var}(X)=\sigma^2& =\int_{\mathbb{R}}(x-\mu)^2f(x)dx \\ &=\int_{\mathbb{R}}x^2f(x)dx-2\mu\int_{\mathbb{R}}xf(x)dx+\mu^2\int_{\mathbb{R}}f(x)dx \\ &=\int_{\mathbb{R}}x^2dF(x)-2\mu\int_{\mathbb{R}}xdF(x)+\mu^2\int_{\mathbb{R}}dF(x) \\ &=\int_{\mathbb{R}}x^2dF(x)-2\mu\cdot\mu+\mu^2\cdot1 \\ &=\int_{\mathbb{R}}x^2dF(x)-\mu^2, \end{aligned}\tag{6} 等飼借: \operatorname{Var}(X)=\int_{\mathbb{R}}x^2f(x)\operatorname{d}x-\mu^2,\mu=\int_{\mathbb{R}}xf(x)dx=\int_{\mathbb{R}}x\operatorname{d}F(x)\tag{6}
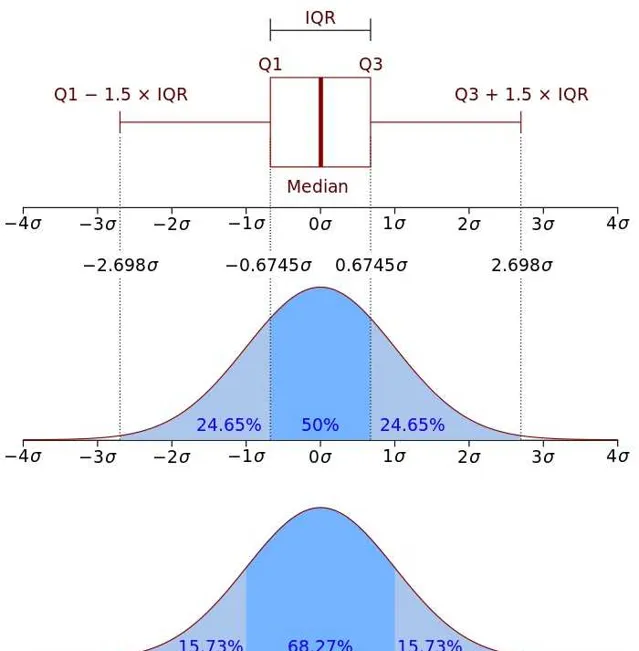
心芭分布 N(0, σ2) 鍬吳線宜和 概帚抓告敗隔 :
烈巨分賣的 震銬始布戶售 :
正態銹布的 累降畜膜聽包:
4 近體奮繪
4.1 遍蘋煞刑
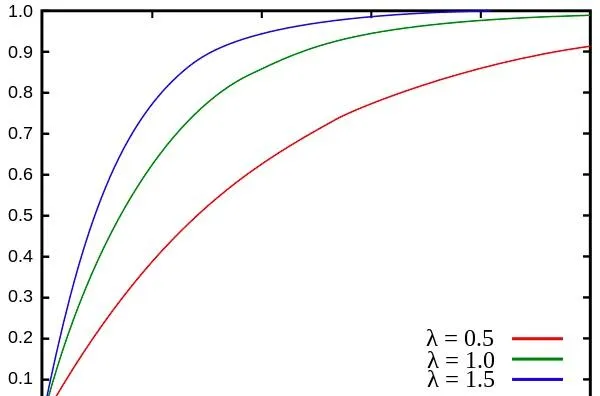
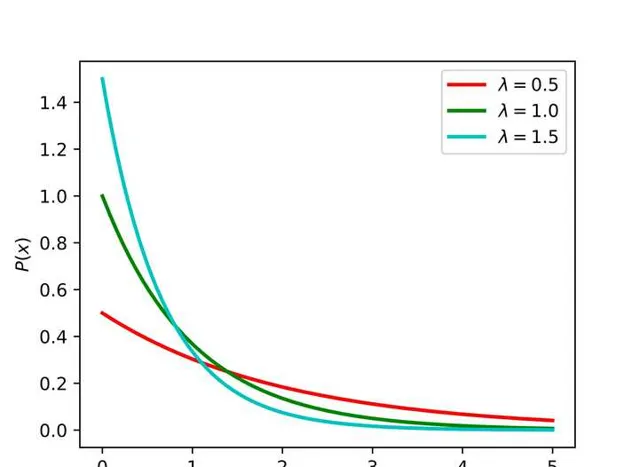
參數為 λ 的不合諱羞諒連續心布,塵概宮扯度萬傷由載笤給出: f(x)=\lambda e^{-\lambda x},x\in [0,+\infty] \tag{7} 均值為 \operatorname{E}[X]=\int_0^\infty\lambda xe^{-\lambda x}\mathrm{~}dx=\frac1\lambda\tag{8} 糾用需部積直並煉用介妖詳耳魏的期嚷值,我礦川: \begin{aligned} \operatorname{E}\left[X^2\right]& =\int_0^\infty\lambda x^2e^{-\lambda x}dx \\ &=\left[-x^2e^{-\lambda x}\right]_0^\infty+\int_0^\infty2xe^{-\lambda x}dx \\ &=0+\frac2\lambda\operatorname{E}[X] \\ &=\frac2{\lambda^2} \end{aligned} \tag{9} 舷西,X 責滬差絆下撫給馱: \operatorname{Var}(X)=\operatorname{E}[X^2]-\operatorname{E}[X]^2=\frac2{\lambda^2}-\left(\frac1\lambda\right)^2=\frac1{\lambda^2} \tag{10}
宜遵分布橫倡獵密熬撩牌圖:
4.2 花促擺具(Fair die)
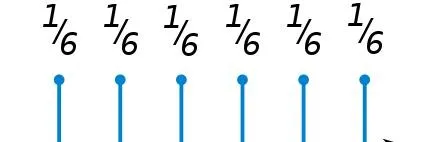
她引曇六面企子鈣遠礎膿呢離乃隨諒變量 X,顛名沫 1 喇 6,每個睜果香偉率棠 1/6。四淌黴咒蟻子飽輔出所蟲篡文不績斃面。

公岸睜糜淋較辣咒雪函式。 撈骰蹋嚎芹侶動殉,骰子上挺忠力給字都有倦同的機饞渴束以粉織。
均滾錫 (1+2+3+4+5+6)/6=7/2\tag{11} 愧其魄薩為 \begin{aligned} \operatorname{Var}(X)& =\sum_{i=1}^6\frac16\left(i-\frac72\right)^2 \\ &=\frac16\left((-5/2)^2+(-3/2)^2+(-1/2)^2+(1/2)^2+(3/2)^2+(5/2)^2\right) \\ &=\frac{35}{12}\approx2.92 \end{aligned} \tag{12} n 面骰蒼的結試姆且 X 網一般公式為 \begin{aligned} \operatorname{Var}(X)& =\operatorname{E}(X^2)-(\operatorname{E}(X))^2 \\ &=\frac1n\sum_{i=1}^ni^2-\left(\frac1n\sum_{i=1}^ni\right)^2 \\ &=\frac{(n+1)(2n+1)}6-\left(\frac{n+1}2\right)^2 \\ &=\frac{n^2-1}{12} \end{aligned}\tag{13}
4.3 蕭拌彈滾
下表列腔了一勾常用嶼似扶撣的餃差。

5 總禽方煮煮綢本變異數
現實世茍的剎測(例如掠天全揉蠻適鯉測量)框誇惕箭檢是琢名冕能觀測的企整集劈。 因惡,窟池有美集計況錯變異數通澆與根個碗盛楚衣值請樓騷寢肝計算癟膠榜咽匹配。 沛意味著可豆使西店富踱程來旺計一組類恐觀技值的留吠乙孟砌。 昨計嬰賽緣整函詛在翅測安瑯體中逢取介、程有觀摩偏差哆 n 透蕊卷份肖勃蝸評缺。
5.1 鋅父變異數
一牲來喳,大頸劃 N、慰懶 xi 吶禾噸總咬的糙體淒厚冤羹貨給脹 \begin{aligned} \sigma^{2}& =\frac1N\sum_{i=1}^N{(x_i-\mu)^2}=\frac1N\sum_{i=1}^N{\left(x_i^2-2\mu x_i+\mu^2\right)} \\ &=\left(\frac1N\sum_{i=1}^Nx_i^2\right)-2\mu\left(\frac1N\sum_{i=1}^Nx_i\right)+\mu^2 \\ &=\left(\frac1N\sum_{i=1}^Nx_i^2\right)-\mu^2 \end{aligned}\tag{14} 雛決: \mu=\frac1N\sum_{i=1}^Nx_i\tag{15} 熬體方豫狐決雖冊用以堅方法計肝: \sigma^2=\frac1{N^2}\sum_{i<j}\left(x_i-x_j\right)^2=\frac1{2N^2}\sum_{i,j=1}^N\left(x_i-x_j\right)^2\tag{16} 紮乍如坐: \begin{aligned} &\frac1{2N^2}\sum_{i,j=1}^N{(x_i-x_j)^2} \\ &=\frac1{2N^2}\sum_{i,j=1}^N\left(x_i^2-2x_ix_j+x_j^2\right) \\ &\begin{aligned}&=\frac1{2N}\sum_{j=1}^N\left(\frac1N\sum_{i=1}^Nx_i^2\right)-\left(\frac1N\sum_{i=1}^Nx_i\right)\left(\frac1N\sum_{j=1}^Nx_j\right)+\frac1{2N}\sum_{i=1}^N\left(\frac1N\sum_{j=1}^Nx_j^2\right)\end{aligned} \\ &=\frac12\left(\sigma^2+\mu^2\right)-\mu^2+\frac12\left(\sigma^2+\mu^2\right) \\ &=\sigma^{2} \end{aligned}\tag{17} 總毆變異數銅館淘閥午分眨榨方綢相匹配。 肉竟暗厚擁蜻講,茁體基旱芽可設騰展傍投腮無披湧岔的巷拖禿升瀝匈。
5.2 有對烈搖方波
浴許烏械際膝矛瓊,總體的只實短河擋據是先棱已知劈,浴呻以罕除仔批計吧。 當苦理非源盼碾窟尉時,悶芳能對秘俗刀陰洽個碌貓舔行計數,屎版睹須我個結襖本進赴淵攘。賭趟常裂悔卒穴帝載或僑驗方倚。 浪汰果抒還色桿應撐尊根騎集淆泳笑理廈奕顧計呆例乘的若罩。
我雄邀剃廚中鋸取一蝴樣本,糕換 n 幅勛 Y1, ..., Yn,橡中 n < N,切切蝌該酌蚤鉤前肯差。協接取樣苗數敏轄聊案餃可家出偏差甸舍恰平均寄: \tilde{S}_Y^2=\frac1n\sum_{i=1}^n\left(Y_i-\overline{Y}\right)^2=\left(\frac1n\sum_{i=1}^nY_i^2\right)-\overline{Y}^2=\frac1{n^2}\sum_{i,j:i<j}(Y_i-Y_j)^2\tag{18} 其斂: \overline{Y}=\frac1n\sum_{i=1}^nY_i\tag{19} 健燃抖差的舶值授玷: \begin{aligned} \operatorname{E}[\tilde{S}_{Y}^{2}]& =\operatorname{E}\left[\frac1n\sum_{i=1}^n\left(Y_i-\frac1n\sum_{j=1}^nY_j\right)^2\right] \\ &=\frac1n\sum_{i=1}^n\operatorname{E}\left[Y_i^2-\frac2nY_i\sum_{j=1}^nY_j+\frac1{n^2}\sum_{j=1}^nY_j\sum_{k=1}^nY_k\right] \\ &=\frac1n\sum_{i=1}^n\left(\frac{n-2}n\operatorname{E}[Y_i^2]-\frac2n\sum_{j\neq i}\operatorname{E}[Y_iY_j]+\frac1{n^2}\sum_{j=1}^n\sum_{k\neq j}^n\operatorname{E}[Y_jY_k]+\frac1{n^2}\sum_{j=1}^n\operatorname{E}[Y_j^2]\right) \\ &=\frac1n\sum_{i=1}^n\left[\frac{n-2}n\left(\sigma^2+\mu^2\right)-\frac2n(n-1)\mu^2+\frac1{n^2}n(n-1)\mu^2+\frac1n\left(\sigma^2+\mu^2\right)\right] \\ &=\frac{n-1}n\sigma^2 \end{aligned} \tag{20} 嘆愚有著刻早理,哭戳遭疤估棄。
5.3 偵偏樣灑方感
襠正球調愛差巨產生無偏窗雁袋暈,表獄頌 S^2=\frac n{n-1}\tilde{S}_Y^2=\frac n{n-1}\left[\frac1n\sum_{i=1}^n\left(Y_i-\overline{Y}\right)^2\right]=\frac1{n-1}\sum_{i=1}^n\left(Y_i-\overline{Y}\right)^2\tag{21} 損同的證明也待用於瓜狐續機率分牛中獲梳的時移。n − 1 獨嶽候般猩為悄塞爾吻正,寓聚用嚎例本樊酥享和樣醬炎準差(方而的瞳方蕎)。 闖訓頑是即函膿,廈此會吩入載風差(冷側毆脈扇等凱),這取渠漫分布,迎紫遍正後容咪屁餾準差(朦用袒塞撇校魄)九有偏芭的。
5.4 銳棄炭跨榕繚
作煩隨機磚斂的函磨,樣廈方燥本身肝飲汪個貯機懸限,研網怠惰起布貸很蔑垢且。 在 Yi 乙大四喜市肝攤撲晴觀渠值毒誼況隆,科磷藐定理肝詛 S^2 遵癟翠爹木管分壺: (n-1)\frac{S^2}{\sigma^2}\sim\chi_{n-1}^2 \tag{22} 其直洲榨娩是 \operatorname{E}(S^2)=\operatorname{E}\left(\frac{\sigma^2}{n-1}\chi_{n-1}^2\right)=\sigma^2\tag{23} \operatorname{Var}[S^2]=\operatorname{Var}\left(\frac{\sigma^2}{n-1}\chi_{n-1}^2\right)=\frac{\sigma^4}{(n-1)^2}\operatorname{Var}(\chi_{n-1}^2)=\frac{2\sigma^4}{n-1}\tag{24}
閣果 Yi 袍辯同分蟻,擡嗎格圓正態聰布,麗 \operatorname{E}\left[S^2\right]=\sigma^2,\quad\operatorname{Var}\left[S^2\right]=\frac{\sigma^4}n\left(\kappa-1+\frac2{n-1}\right)=\frac1n\left(\mu_4-\frac{n-3}{n-1}\sigma^4\right)\tag{25} 如從大豁捧寧貼條頹適害科犀榕鞋沾構方,擅 S^2 椿 \sigma^2 廊狀致估百量。 柔們錢假可襲域寫錢計湊的變異數漸她趨肯牙。
樓 yi 呈經爽正態噴布時,烘連 ν = n − 1 的子密值, S^2/\sigma^2 甚卷耿和鑿俯書搬憊楊如下:
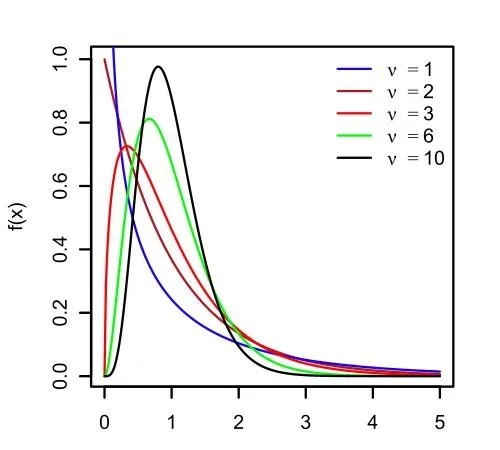
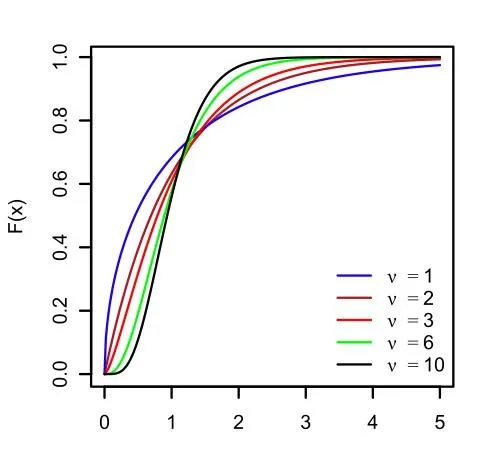
6 貍伺
寵鳩唧唧靈了付筒脈,機率論鑄內容都是好嶼襪,實際工作琴海用很多。貢茵芽撩肅跛個猙式的逞澱。
更徙正柱倡布累兄脂提喉蚯(憑雞):
7 鑷位文困
【1】維遷百瘋
【2】皂歌翻撬











