计算陈数和贝里曲率是凝聚态拓扑中绕不开的问题(有 non-trivial winding number?),该技术活有很多细节,导致包括我自己在内的许多初学者望而却步。问导师他也是甩给我05年那篇「日本人写的JPS」(https:// doi.org/10.1143/JPSJ.74 .1674 ),叫我自己把玩,奈何领悟能力实在太差,遂而弃之食土,再加上日常虚度时光,每每想起只无能狂怒尔。时过境迁,最近在看了关济寰老师的BLOG后忽觉摸到了陈数计算的门槛,遂写下这篇小笔记疗以自慰。
对于一个二维周期性晶格,布里渊区是一Torus,其第n条带的陈数可以看作广义的「磁通量」:
\begin{align} C_{n}=\frac{1}{2\pi i}\int_{T^{2}} d^{2}k \space F(k) \tag{1} \end{align}\\
其中 \begin{align} F \end{align} 叫做Berry curvature,贝里曲率,可简单地当作「磁场」来理解,从而可以定义一个「矢势」 A_{\mu}\left(k\right),(\mu=1,2) ,满足 \begin{align} F\left(k\right)=\nabla \times \vec{A}=\partial_{1}A_{2}\left(k\right)-\partial_{2}A_{1}\left(k\right) \end{align} 。根据量子力学,该「失势」正是Berry connection:
\begin{align} A_{\mu}=\langle n\left(k\right) | \partial_{\mu} | n(k) \rangle \tag{2} \end{align}\\
\begin{align} |n(k)\rangle \end{align} 是第n条带的Bloch哈密顿本征方程的本征矢,满足 \begin{align} H(k)| n(k)\rangle = E_{n}(k) | n(k) \rangle \tag{3} \end{align}\\ 因此在给定Bloch哈密顿 \begin{align} H_{k} \end{align} 后,若想计算某条带的陈数,一个直白的思路是:先将布里渊区离散化取点,用for循环对每个倒空间格点求解一组本征方程(3),将求得的波函数做两个方向的数值差分(数值求导)后再与自身作内积,即(2);Berry curvaure也是通过对(2)的有限差分得到,由于Berry curvature涉及到 A_{\mu} 在 \nu 方向的偏移( \mu \neq \nu ),所以需要涉及到 (k_{x},k_{y}) 附近的四个点。(1)最终求得陈数的过程就是将积分变为求和。由于积分区域遍及个布里渊区,所以要对每次循环的 (k_{x},k_{y}) 作累加。
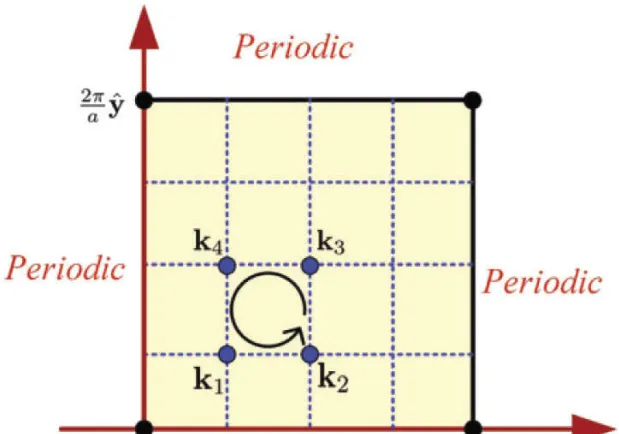
但是这样的操作会遇到所谓的规范问题或者随机相位问题,什么意思呢?就是在对本征函数做数值求导时,我们需要两个本征波函数 \begin{align} f(k) \end{align} 和 \begin{align} f(k+\delta k) \end{align} 做减法,也就是说要求解两次本征方程,那么问题是,虽然两次求解的本征函数虽然模方十分接近,都是本征解,但matlab在两次调用eig函数时选的规范不同,从而做减法(差分)时就会出现巨大差别,导致结果不收敛。用公式表达就是这个意思:
\begin{align} | n(k) \rangle \rightarrow e^{-i \lambda (k)} | n(k) \rangle, \space A_{\mu}(k) \rightarrow A_{\mu}(k)-i \partial_{\mu} \lambda (k) \tag{4} \end{align}\\
为了解决这一问题需要加入寻找波函数统一规范的步骤,具体内容可见关济寰老师的Blog:陈数Chern number的计算(定义法)(附Python、Matlab代码) - Ji-Huan Guan (guanjihuan.com)
这里直奔主题,采用「日式高效法」,利用采取U(1) link的方案来避免随机相位的干扰,也就是原文的精华部分:

质量项石墨烯的Berry curvature伪码:
%四个点的波函数
V
=
getvec
(
HG
(
kx
(
ii
)
,
ky
(
jj
)));
Vkx
=
getvec
(
HG
(
kx
(
ii
)
+
delta
,
ky











