瀉藥。強化學習(RL)在遊戲領域上已經取得了巨大成功,比如下圍棋;但是目前在現實問題上的套用還有很多困難。俞老師有一個很有名的回答:強化學習領域目前遇到的瓶頸是什麽?

據我的觀察,現實任務相較於遊戲,最大的挑戰就是stochasticity(隨機性)。這篇文章我就用我們最近的工作作為例子來講一下用RL解決現實問題的一些經驗,包括怎麽去建模現實問題、什麽是隨機性、解決的演算法應該有怎樣的性質、base model怎麽選等等。
這裏有一個選擇:RL可以用來做pre-training和post-training,但是post-training更親民一點,作為科研乞丐我也只能玩的起微型的post-training,比如這份工作從頭到尾用的GPU甚至沒超過13G,一張T4就夠了。但是模型小並不代表效能差,關鍵還是怎麽去建模這個問題然後選擇合適的演算法。例如我們把這個小模型的效能從18%(跟GPT-4水平差不多)直接飆到了82%,翻了好幾倍。現在LLM無腦堆數據和模型,我感覺還是有不少別的東西可以做的。如果大家關心工作的內容,也可以先看看我們的website,有很多demo和可以玩的東西:https://digirl-agent.github.io。
現實環境中的RL困境
Stochasticity
RL目前打遊戲很強,而遊戲往往是符合某種可預測的規則的。比如下圍棋,規則是放在那裏的,你下5行4列的黑子,這個黑子就會出現在5行4列;玩atari也是,你按一下往右的按鍵,人物就一定會往右一格。但是real-world的task不一定,會有 幾乎無限 的擾動,比如如果你要買一個東西,輸入物品名字後淘寶每次會給你推不同的東西。現在很多的RL工作做機械臂的一些模擬,都是在同一個工作台上做實驗,如果換一個桌面環境,就秒掛了。但是現實任務下,幾乎沒有辦法避免環境中出現隨機性,因此應該去 顯式地建模這種隨機性 (將解決隨機性作為任務的一部份)。為了體現隨機性,我們選了一個用手機完成查資料、購物這些現實任務的方向(之前沒有人在這個上面做過RL),這個任務的所有環境都是在手機模擬器裏面執行的,所以使用者自己玩會出現的各種隨機性,環境都會建模進去。一些比較典型的隨機性有這些:

比如網頁過一段時間主頁會變,這個會導致每次點選網頁同一個地方都可能看到不同的結果,比如前兩張圖,有時候網頁上面的廣告只有兩行,有時候有三行,這樣會導致整個網頁的布局變化;再比如後面有幾張圖,有時候網頁會有彈窗或者廣告,必須先解決掉才能繼續;又比如商品每次搜尋的順序都可能不同,是根據伺服器的推薦演算法排序的。這些隨機性會導致直接behavior cloning比較困難,直接用monte carlo去做RL也很困難,因為之前monte carlo用的data很可能沒法generalize到stochastic的情況上。
Scale
要解決stochasticity,一般來說需要 巨大的數據量 。可以這麽理解:每一個可能存在stochasticity的自由度都需要一批cover到盡可能多情況的數據進行擬合。比如上面提到的google彈窗,理想情況下我們應該盡可能多地收集在google頁面可能彈出的彈窗,以及成功的trajectory是怎麽解決這些彈窗的。當類似這樣的stochasticity的量多起來時,所需要的數據也是成倍增長的。要解決這個問題,如果用offline RL,顯然需要大量數據;如果是online RL,那每次training間隔時收集的數據也是越多越好:因為如果有偏地建立對stochasticity的表示,一定會降低collected trajectory的質素。
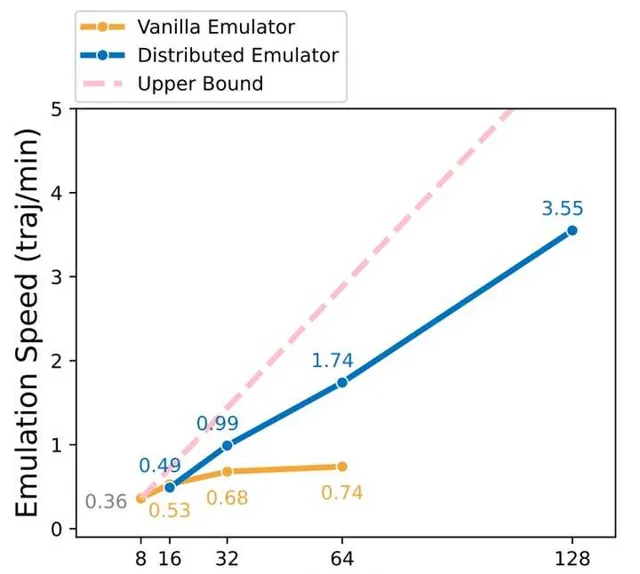
例如我們的工作中,為了解決這個問題,就專門寫了一個多機distributed parallel的指令碼,支持多機大規模收集trajectory。例如一台機子能開8個安卓模擬器的話,可以輕松scale到四機甚至十六機,收集速度是線性增長的,而且不需要任何GPU。我們對比了只在一個更多CPU的機子上開更多的模擬器的方案,這個單機方案的速度是logarithm增長的,比我們的方法慢很多,在repo裏面有詳細的分析:digirl/multimachine/README.md。工作早期四天的訓練,有了多機支持,後面只需要兩天甚至一天就搞定了。
Reward: Step-level or Trajectory-level?
之前在Jiayi的工作裏面大家嘗試了用step-level reward去解這個問題,但是發現evaluator很難正確地給出reward。比如如果我們要查詢淘寶上某一個商品的價格,那麽從淘寶跳到百度應該是一個負的reward;但是百度搜尋也是可以找到淘寶的商品的,只要給一個「淘寶」的關鍵字就可以了(有時候甚至不需要關鍵字搜出來的也都是淘寶的結果)。這使得這個reward具體的數值很難確定(有時候甚至正負也不好確定)。因此我們認為應該將reward做成trajectory-level的,因為 判斷「一個任務是否成功」比「這一步是否更靠近結果」簡單很多 ,現在的LLM例如Gemini都可以完美解決了;而對於step-level上是否離目標更近,LLM還不太行,所以應該轉而交由一個專用演算法解決,例如訓練一個很靠譜的critic。
小模型能否逆襲?
「小」不一定「差」
大家會好奇我們用的是什麽模型,好像想要解這個問題,需要一個很fancy的模型架構。其實我們用的模型非常小而且樸實,參數加起來才 1.5B,一張T4就能跑 ,無lora的training才用了13G的vram。模型的架構是一個freeze的CLIP配一個要tune的T5,之前一個大哥pre-train的,模型名字叫做AutoUI。模型的輸入是一張當前和上一個state的手機的螢幕截圖 + 上一步的action + 最終的goal。模型會輸出接下來要做什麽,例如文字或者座標。 註意輸出的是座標,比如[528, 129],螢幕上是沒有任何提示的。 之前的工作,例如GPT,都是螢幕上有很多tag,讓GPT去選一個出來,比如GPT的螢幕被弄成了這樣來讓他好做一點:
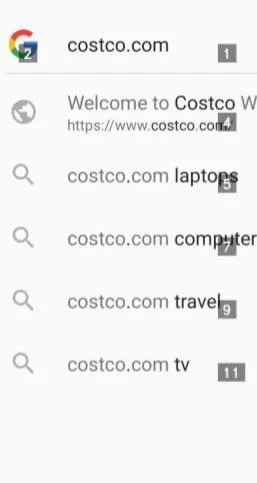
我們的是沒有這些tag的,直接輸出一個text形式的座標。這個難度要大得多,也更realistic一點,但是我們一個1.5B的模型直接把GPT幹趴了,領先三倍多(詳見後面的結果部份)。大模型固然好,但也不是人人都玩得起的,這個結果充分說明了一個專精的模型不需要很大。當然,如果要scale到general tasks,可以想像1.5B的容量還是有點小了。
選擇base模型的一些通用建議
這裏我有一些選base模型的建議,首當其沖的就是 base模型的效能不能太差 。如果policy initialization太差,那麽采集到的trajectory大概率是錯的,這個時候RL必死無疑,不管你用什麽演算法都救不回來,沒有data拿什麽學。那怎麽獲得一個還可以的policy initialization?往往需要先從human/很厲害的模型(比如GPT-4)那邊用監督學習學到一點知識,然後再上RL。比如我們的工作中,大概的流程是這樣的:
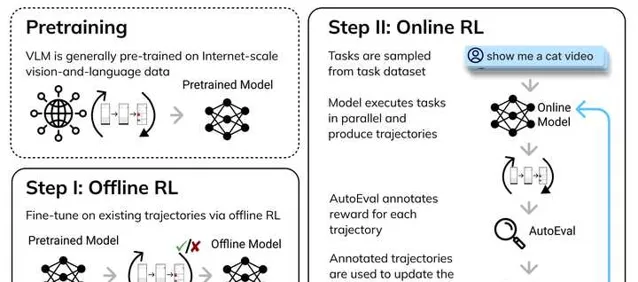
務必先拿一個稍微靠譜的pre-trained模型 (效能有10%以上),然後RL。如果效能太差(比如只有1%),還是早點換一個base model比較好,不然不知道要學到什麽時候。有同學會問為什麽自己上課時作業裏遇到的RL可以用random initialization:這是因為遊戲的action space很小,盲猜也能對的。在real-world problem上一抓幾千個potential action,給random policy直接幹玉玉了。
第二個是 base模型的大小不能太大 。一個原因是模型大,就需要更多的data去fit,簡稱訓不動。特別是online RL,所有data都是邊訓邊收集的,如果model需要成倍的數據,那麽collect也會需要成倍的數據,這需要很多機器一起跑collection。如果想偷懶少收集一點,那得調learning rate,可能更痛苦。試想你跑一輪實驗需要一個星期,還要不要畢業了。另一個原因是窮。這個就不太需要解釋了。作為一名合格的科研乞丐,我深刻認識到窮是不需要任何解釋的。
演算法
這一部份會稍微燒腦一點,可能需要反復讀幾次。我會把用到的知識都做成link放在旁邊。
Filtered AWR
環境的基礎搭好以後,就可以著手思考什麽樣的演算法適合這個問題了。一個能想到的最簡單的解法就是filtered behavior cloning(filtered BC),就是讓模型自己玩,玩對了就拿對的整條trajectory讓模型去學習自己是怎麽做對的,玩錯了就扔掉這個數據。train的方法也很簡單,直接用language modeling的老方法去訓練即可。但是filtered BC有兩個問題:第一是只要trajectory成功了,那麽其中的每一步,不管好壞,都會被模仿到;第二是沒法高效地建模stochasticity,因為沒有critic去專門fit這種隨機性。
因此我們想到了, 可以不使用最終的reward,轉而使用advantage去filter data 。這種演算法會產出一個模型,這個模型在infer時的架構與原來完全相同,不需要為了RL往模型裏面加新的module;而在train時,我們可以加入critic來估計這個advantage,從而用這個advantage來filter data;然後用這個filtered data來用和BC一樣的loss訓練模型。這是一個非常簡單的想法,靈感來源於AWR(沒聽說過的同學可以略看這篇:AWR(Advantage-Weighted Regression)演算法詳解與實作),但是我們把AWR硬化成了hard filtering。
GAE的通俗理解
現在我們就要思考如何去設計這個advantage了。前面提到了stochasticity的問題,其實有關隨機性,RL的前人已經有過非常多的討論,其中John Schulman的GAE(Generalized Advantage Estimation)很大程度上緩解了隨機性的問題。對GAE還不了解的同學強推這篇:張海抱:【強化學習技術 28】GAE。其實GAE本質上就是下面這一串advantage estimate的加權平均:
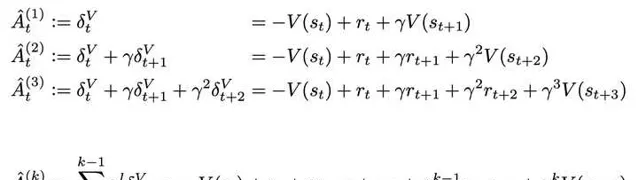
其中, \hat{A}^{(k)}_t 稱為 k -step advantage。 當 k=1 時,就是1-step TD;如果我們把 k 拉到無窮大,那其實就是 t 時刻的monte carlo estimate \sum_{l=0}^{\infty}\gamma^lr_{t+l} 減掉baseline V(s_t) 。 這體現了GAE 「generalized」的原因:將advantage考慮成TD和MC的某種融合。因為MC是低bias的,TD是低variance的,所以可以根據實際情況調這個比重。
GAE被當成各種baseline(包括PPO也用GAE)是有原因的 - 在實驗中,我們發現GAE用來做real-world task效果比單純的TD/MC的estimate要好不少,因為TD很大程度上看value的準確度,而因為現實任務下的訓練數據非常noisy,這個value critic是極難學的。這個時候就需要MC過來幫忙。但是單純的MC又是不行的,因為現實任務有隨機性,之前拿到的data沒法generalize到隨機出現的情況。
GAE的簡化
我們的state-level advantage就是受到GAE的啟發, 只取了GAE的第一項和無窮項 。對於每一個state action pair,我們取它的MC return advantage \sum_{t=h}^H r(t) = r(s_H,a_H, c) (這個是因為我們是trajectory-level reward,只有最後一步reward可能為1)和one-step TD advantage V(s_{t+1}, c)+r(s_h,a_h,c)-V(s_h,c) ,兩者weighted sum可得
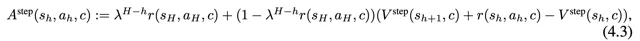
我們發現這個簡化版的GAE能夠比較robust地估計每個step的advantage。從行為的角度看,MC使得如果trajectory是成功的,那麽其中的每一個step都會有比較大的advantage(在實踐中我們發現,這樣導致不成功的trajectory基本沒有機會,這是件好事);TD使得critic認為value gain比較大的transition會獲得更大的advantage,從而相對更不會被filter掉。下面是一個例子:
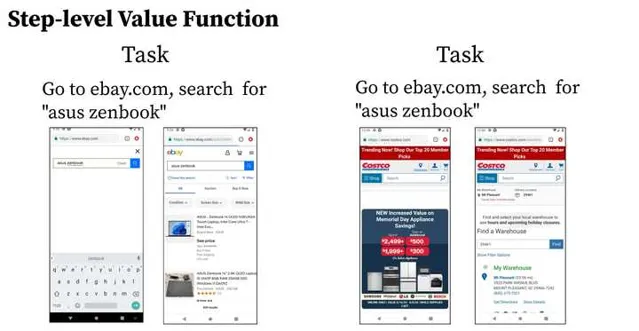
左圖中要買一個筆記電腦,agent從搜尋框跳到商品展示頁面,我們發現演算法給了一個正的transition difference;右圖中也是買一個筆記電腦,但是agent點錯了,從costco的主頁跳到了網址列,這個時候我們發現演算法給了一個負的transition difference。這些都是比較符合我們設計的結果。由於這些filter都是step-level的,我們將這裏的critic稱為state-level value critic。
Automatic Curriculum
在實踐中,我們發現了另外一個問題:由於我們訓練時用的task是從task set裏randomly sample出來的,所以 當一個task已經被完全掌握了以後,重新sample到不會帶來很大的提升 ,也就是說正資訊量比較小。因此我們的filter同時需要過濾掉那些經常成功的trajectory。但是,如果一個task沒做對,它帶來的資訊量大概率是負的。要同時考慮這兩種情況,就可以設計一個簡單的instruct-level advantage:
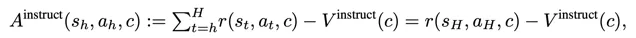
其中這個instruct-level value critic直接去 回歸task的成功率 即可。這個演算法的一個妙處在於,一個簡單的task會在早期被解決,這個時候它應該被學到;一個稍微難一點的task在早期沒法被解決,但是由於早期的任務解決後,模型透過automatic curriculum有更多資源去學習更難的task,從而加速中期task的解決,但這個時候依然無法解決最難的task;等中期的也被解決的差不多後,訓練資源又會向最難的方向傾斜。一個訓練到中期的automatic curriculum的功能大致如下:

如圖,在中期階段,最簡單的task已經學會了,因此這個instruction(也就是task)的value會比較大,導致instruction-level advantage小;較難的task在這個階段做對了以後會有更小的instruction value,因此反而可能不被filter掉。在實操中有一個細節,如果是offline-to-online的學習,那麽offline階段不要用instruction-level critic,因為模型一開始還沒有學會最簡單的task,而pre-collected data裏面有很多成功的簡單的task,這會導致filtered buffer損失大批簡單task的trajectory,模型被critic坑了,完全學不到。在fully online的學習下這倒不是個問題,因為critic的學習和模型一樣,也是漸進的,一開始大家的value都小,那成功了也就都會進buffer。
其實Automatic Curriculum是從更大的尺度上在解決stochasticity的問題,因為解決stochasticity需要scale,而大家的計算資源都是有限的。如果一個簡單的task已經被解決了,那麽它一定在可觀察的範圍內已經解決了stochasticity的問題,那麽更多的計算資源應該被分配到更難的task上,因為更難的task往往難在更強的stochasticity。
組裝
接下來,將instruction-level advantage和step-level advantage分別依次用來做filtering,剩下來的高質素數據就能直接用MLE loss訓練模型了。所有的程式碼都開源到github了,歡迎來看源碼。

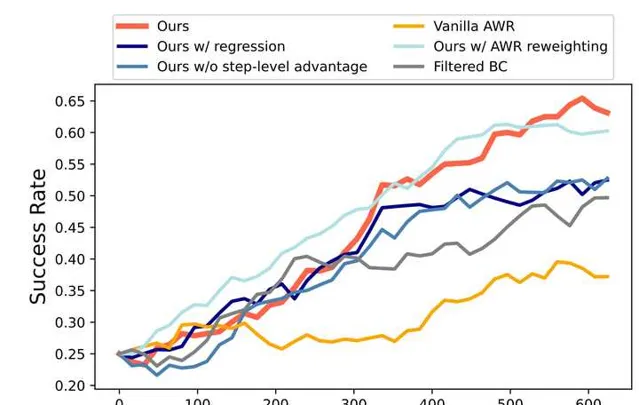
我們把演算法和很多baseline比了一下,發現了很consistent的提升,最後的演算法是最有效的:
結果
我們的結果不僅遠超GPT-4V/Gemini這種off-the-shelf agent,而且比在相同數據集(但是他們是用的pre-collected數據,我們是interactive去收集的)上訓過的CogAgent也強一倍多。filtered BC在這裏也是我們的baseline,因為我們想要看看這種critic-based filter RL的方法究竟帶來了多少好處,結果也是普遍高了10分左右。
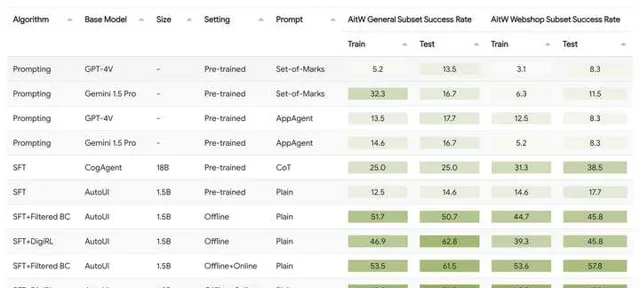
Online learning curve大概分別長這樣(我們目前測了aitw這個task集的兩個subset,左邊一個右邊一個):
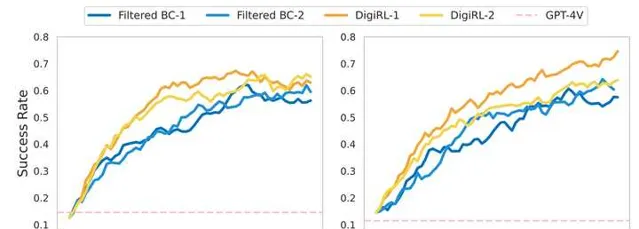
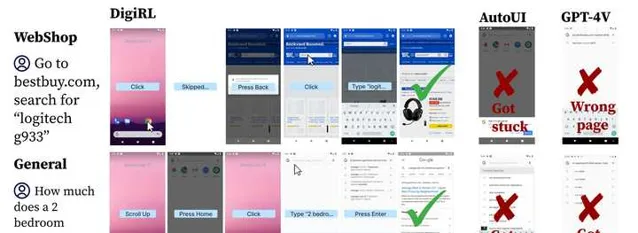
一些qualitative的結果:
資源
非常歡迎大家入坑!我們提供了全套環境、模型、演算法程式碼,並且公開了模型checkpoint和pre-collected data,可以快速啟動。 一張T4就夠,這不抓緊star起來 ;p
GitHub: https:// github.com/DigiRL-agent /digirl









