这篇打算简单叙述量子算法近年的主要进展 (之一), 即量子奇异值变换 (quantum singular value transform) [1] . 故事的起点是这么一件事: 给定某个随机算法, 我们总是可以通过多次重复运行它来提高成功概率. 那么, 我们能尽可能少的重复吗? 量子算法中著名的振幅放大 (amplitude amplification) 技术 [2] 可以提供平方时间加速, 这里技术的例子之一就是 Grover 算法 (或者说"无结构搜索"算法).
这个技术做得事情就是在某个 圆周 上做多次 固定角度 逆时针旋转, 以期在若干次后到达圆周的顶点. 但这么做有个问题, 就是如果我们并不知道"固定角度"到底是多少的话, 我们并不能直接通过连续多次旋转到达顶点附近 – 直到量子奇异值变换 (quantum singular value transform) 相关技术 [3] 的出现解决了这一问题, 方案有些出人意料: 只需要 把圆周"撑成"球面 , 然后在上面绕着某两个轴交替旋转, 可以证明这样的旋转会在球面的极点附近收敛. 这即是不动点振幅放大 (fixed-point amplitude amplification) [4] 技术.
为什么这跟奇异值分解有关呢? 简而言之, 上面所切换的两个旋转轴, 其实跟某个矩阵的奇异值分解 (singular value decomposition) 的左奇异矢量及其正交矢量张成的平面, 以及右奇异矢量及其正交矢量张成的平面有关.
本文亦发表于我的博客: 如何提高成功概率:量子奇异值变换简说.
下面开始正文.
以平面旋转来提高成功概率
给定某个成功概率为 p 的随机算法, 为了提高它的成功概率 (譬如说成功概率接近 1 ), 我们可以这么做: 将这个算法重复允许很多遍, 如果其中有一个拷贝是成功的话, 我们就认为这个新的随机算法是成功的. 不难证明, 如果我们重复允许这个算法, 直到某一次成功才停下来的话 (满足几何分布),那么期望重复次数是 1/p .
我们能在其他模型下做的更好吗? Gilles Brassard 和 Peter Høyer 在 1997 年证明了 [2] , 对于量子算法, 我们只需要"重复" O(1/\sqrt{p}) 次. 对量子算法稍有些了解的读者不难意识到, 著名的 Grover 算法其实是这一问题的特殊情况 [5] , 同样提供了关于时间复杂度的平方加速. 具体来说, 这一问题可以写作:
任务 1 . 给定可逆量子算法 U:|0\rangle^{\otimes k} \mapsto \sqrt{p}|1\rangle|\psi_{\rm good}\rangle+\sqrt{1-p}|0\rangle|\psi_{\rm bad}\rangle 使得对于选定的初始态 |\psi_{\rm init}\rangle 和目标态 |\psi_{\rm final}\rangle , 这一量子算法的成功概率是 p=\langle \psi_{\rm final}|U|\psi_{\rm init}\rangle . 那么我们可否构造一个 U' , 在尽可能少的调用 U 的情况下, 使得 \langle \psi_{\rm final}|U'|\psi_{\rm init}\rangle 非常接近 1 .如果取 |\psi_{\rm final}\rangle 为 |\psi_{\rm good}\rangle 的话, 不难发现这个问题有个很漂亮的几何解释:
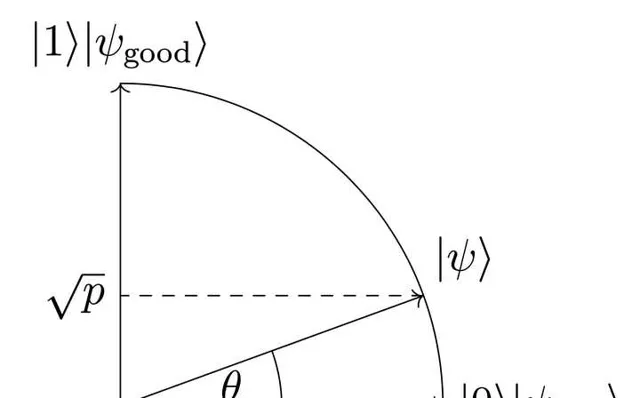
即 |1\rangle|\psi_{\rm good}\rangle 和 |0\rangle|\psi_{\rm bad}\rangle 其实可以张成一个平面上的圆, 它们分别对应于圆上的两点; 而 |\psi_{\rm init}\rangle 当然也可以投影到这个圆上. 换而言之, 问题变成了, 我们能够设法使得从圆心指向 |\psi_{\rm init}\rangle 的矢量, 能够绕着圆心旋转到 |\psi_{\rm final}\rangle ? 这里的量子算法 U 其实描述的就是这个旋转过程 -- 展开来说, 这里通常包括绕着两个轴 |0\rangle|\psi_{\rm bad}\rangle 和 U|0\rangle^{\otimes k} 反射, 然后交替这两个反射过程, 即作用 Grover 算子 G_U=U(2|0\rangle\langle 0|^{\otimes k}-I_k) U^{\dagger}((2|0\rangle\langle0|-I_1)\otimes I_{k-1}) , 就会绕着圆心逆时针旋转.
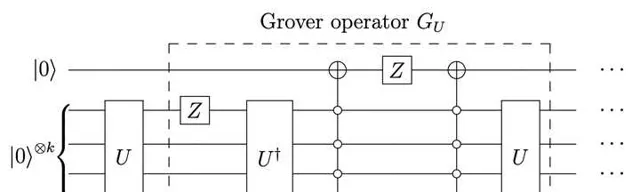
但是上面的旋转算法有个问题, 为了计算需要旋转多少次, 我们需要知道 Grover 算子每次会在这个圆上逆时针旋转多少度. 但总有些时候我们并不知道旋转角度, 也就是说, 如果我们 连续地 用 Grover 算子作用在 同一个圆 上 (所谓 fixed-point) 转的话, 很可能总是会转过头的.
于是, 有更好的办法吗?
量子奇异值变换和分解定理
上面的振幅放大 (amplitude amplification ) 其实只考虑了二维的希尔伯特空间, 或者说一个量子比特. 令人惊讶的是, 在很多时候其实我们只需要考虑二维空间, 譬如说 Jordan 引理 [6] 就告诉我们, 对于两个投影算子 \Pi_1,\Pi_2 , 他们所作用的希尔伯特空间可以被正交分解成一群一维不变子空间和一群二维不变子空间; 这些不变子空间的维度取决于他们对应的 \Pi_1\Pi_2 的特征值是否为 0 或 1 , 如果都不是的话是二维, 否则是一维.
Jordan 引理可以用来做一些很神奇的事情, 譬如用同一个"证据"态 (witness state) 来做 \mathsf{QMA} 的 error reduction [7] , 或者来对量子零知识证明来做 rewinding [8] . 是的, 这些应用听起来很反直觉, 因为把量子线路作用到量子态后, 再做测量通常会把量子态弄得面目全非; 但这里的分解定理告诉我们, 在一些情况下, 量子态们只会在二维子空间里跳来跳去. 这也意味着我们可以设法重复利用这些量子态们.
András Gilyén, Guang Hao Low, 宿愿和 Nathan Wiebe 在 2018 年的工作 [1] 把上述 Jordan 引理推广到了更一般的情形, 即
如果在投影算子 \Pi_1 和 \Pi_2 之间再插一个酉算子 U 的话, 它们所作用的希尔伯特空间还是可以分成一群一维不变子空间, 和一群二维不变子空间.有趣的是, 这里的不变子空间的维度, 跟它们对应的 \Pi_1 U \Pi_2 的奇异值分解中对应的奇异值是否为 0 或 1 有关: 如果都不是的话, 那么不变子空间的维度是二维.
展开来说, 考虑 \tilde{\Pi} U \Pi 的奇异值分解, 即 \tilde{\Pi} U \Pi = \sum_{i=1}^{d_{\rm min}} \sigma_i |\tilde{\psi}i\rangle\langle \psi_i| , 其中d_{\rm min}=\min\{d,\tilde{d}\} , 并且 d:={\rm rank}(\Pi) 和 \tilde{d}:={\rm rank}(\tilde{\Pi}) . 对于奇异值满足 0 < \sigma_i < 1 的情形, 分别可以定义 |\psi_i\rangle 的正交矢量 |\psi_i^{\perp}\rangle := \frac{(I-\Pi)U^{\dagger}|\tilde{\psi_i}\rangle}{\sqrt{1-\sigma_i^2}} , 以及 |\tilde{\psi}_i\rangle 的正交矢量 |\tilde{\psi}_i^{\perp}\rangle:=\frac{(I-\tilde{\Pi})U|\psi_i\rangle}{\sqrt{1-\sigma_i^2}} , 其中奇异值 \sigma_i^2 = \langle \psi_i | U \Pi U^{\dagger} | \tilde{\psi}_i\rangle . 也就是说左奇异矢量对应是不变子空间是 \tilde{H}_i:={\rm span}(|\tilde{\psi}_i\rangle,|\tilde{\psi}_i^{\perp}\rangle) , 右奇异矢对应的不变子空间是 H_i:={\rm span}(|\psi_i\rangle,|\psi_i^{\perp}\rangle) ; 而 U 则是从 H_i 跳到 \tilde{H}_i , 同时作用旋转矩阵 R(\sigma_i):=\begin{pmatrix} \sigma_i & \sqrt{1-\sigma_i^2}\\ \sqrt{1-\sigma_i^2} & -\sigma_i \end{pmatrix} .
于是我们可以重新审视上一节中的 Grover 算子 G_U=U(2|0\rangle\langle 0|^{\otimes k}-I_k) U^{\dagger}((2|0\rangle\langle0|-I_1)\otimes I_{k-1}) . 其实它可以被推广为下述形式: e^{i \phi_1(2\tilde{\Pi}-I)} U \Pi_{j=1}^{(n-1)/2} \left( e^{i \phi_{2j} (2\Pi-I)} U^{\dagger} e^{i\phi_{2j+1}(2\tilde{\Pi}-I)} U \right) , 其中 e^{i\phi_k(2\Pi-I)} 等于先作用 \mathrm{C_{\Pi}NOT} , 然后在控制量子比特上作用 e^{-i\phi_k\sigma_z} , 然后再作用 \rm C_{\Pi}NOT . 注意到 \phi_k=\pi 的时候, 我们有 e^{i \pi \sigma_z}=2|0\rangle\langle 0|-I ; 即旋转角度 \{\phi_i\}_{i=1}^n 都取 \pi 的时候, 就是振幅放大 (amplitude amplificatio) 算法. 这意味着我们有一些额外的自由度, 来控制这样的量子算法的表现.
现在, 让我们聚焦到量子奇异值变换中的分解定理导出的那些二维不变子空间们. 注意到左奇异值矢量及其正交矢量可以张成一个平面 (右奇异值矢量及其正交矢量相同), 在这两个平面上我们同样可以考虑他们类似振幅放大算法中的圆; 但是这里我们可以在在这两个不同的平面上绕着圆心旋转 (即作用 2\tilde{\Pi}-I 或 2\Pi-I ), 并且可以通过作用 U 和 U^{\dagger} 来交替切换平面. 那么有没有办法来控制不同的平面的旋转角度呢? 或者说, 给定一组旋转角度, 我们能有办法知道这一系列操作最终做了什么吗?
Isaac Chuang 和 Guang Hao Low 更早的工作 [3] 给出了二维不变子空间中的答案. 事实上上述操作序列可以看成 量子信号处理 (quantum signal processing); 换而言之, n 次不同平面上的交替旋转操作, 相当于对奇异值 \sigma_l 作用了某个 n -次多项式 P , 即 \prod_{j=1}^n e^{i\phi_j \sigma_z} R(\sigma_l) = \begin{pmatrix} P(\sigma_l) & \cdot\\ \cdot & \cdot\ \end{pmatrix} . 更进一步, 借助量子奇异值变换给出的分解定理, 我们可以对所有不变子空间都做类似的操作, 即 f^{(SV)}(\tilde{\Pi} U \Pi)=\sum_{i=1}^{d_{\rm min}} f(\sigma_i) |\tilde{\psi}_i\rangle\langle\psi_i| .
下面我们将给出量子奇异值变换的一个具体应用, 即怎么解决不动点振幅放大 (fixed-point amplitude amplification) 问题.
以球面旋转来提高成功概率
回忆一下, 第一节提到的可逆量子算法 U 的形式是 U:|0\rangle^{\otimes k} \mapsto \sqrt{p}|1\rangle|\psi_{\rm good}\rangle+\sqrt{1-p}|0\rangle|\psi_{\rm bad}\rangle . 换而言之, U 的奇异值分解一定会得到对应于左奇异矢量 |\psi_G\rangle:=|1\rangle|\psi_{\rm good}\rangle 和右奇异矢量 |\psi_0\rangle:=|0\rangle^{\otimes k} 的奇异值. 此时这一可逆量子算法的成功概率 p 满足 \tilde{\Pi} U|\psi_0\rangle=p|\psi_G\rangle , 其中 \tilde{\Pi}:=|1\rangle\langle 1|\otimes I . 也就是说, 为了放大这一可逆量子算法的成功概率, 我们需要下述奇异矢量变换:
任务2 . 构造一个奇异矢量变换 Q , 使得对于任何喂进去的左奇异矢量, 都能吐出对应的右奇异矢量.对于任务 2, 我们需要某个函数, 使得所有奇异值都能被替换为 1 . 又注意到奇异值变换中的奇异值都是非负的 (因为 A 的奇异值变换是用 A^{\dagger} A 定义的), 看起来 sign 函数正好能满足我们的需求:
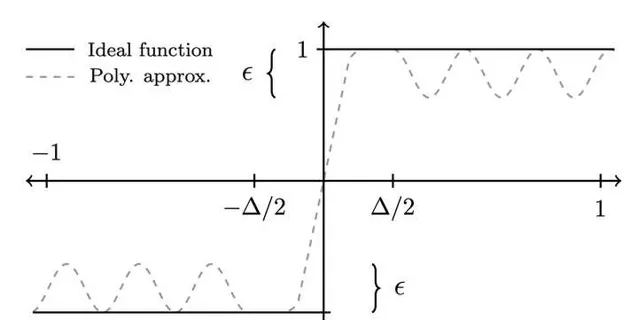
Sign 函数即对于所有大于零的输入输出 1, 对于所有小于零的输入输出 -1. 而在上一节的讨论中, 我们知道每个奇异值变换的一系列旋转操作最终对应于某个多项式函数. 也就是说, 我们需要做的是找到某个多项式函数, 使得其能够很好地近似 sign 函数.
幸运的是, 选取合适参数的高斯误差函数 {\rm erf}(kx):=\frac{2}{\sqrt{\pi}} \int_0^{kx} e^{-t^2} {\rm dt} 就能很好地近似 sign 函数, 而高斯误差函数亦能很好地用多项式函数近似. 即我们可以找到能在 [-1,1]\setminus (-\delta,\delta) 区间内以 \epsilon 误差近似 sign 函数的次数为 O(\log(1/\epsilon)/\delta) 的多项式. 这意味着我们可以通过这一具体的多项式, 选择量子奇异值变换中所需要的一系列旋转角度. 再注意到 \tilde{\Pi} U \Pi = p|\psi_G\rangle\langle\psi_{\rm init}| , 其中 \Pi=|\psi_{\rm init}\rangle\langle \psi_{\rm init}| , 从而我们给出了任务 2 所需要的构造. 即我们找到了某种基于量子算法的神奇"重复方式", 使得我们最终得到的结果矢量总是很接近目标矢量, 不管我们到底重复了多少次.
这样的做法有什么几何解释吗? 从上一节中我们知道, 量子奇异值变换可以看成现在某个平面上 (对应于某法向量) 以选定角度旋转; 再跳转到另一个平面 (对应于另一个法向量) 上, 以另一个选定角度旋转; 以此类推. 有趣的是, 在 Isaac Chuang 等人的综述 [9] 中指出下述几何解释:
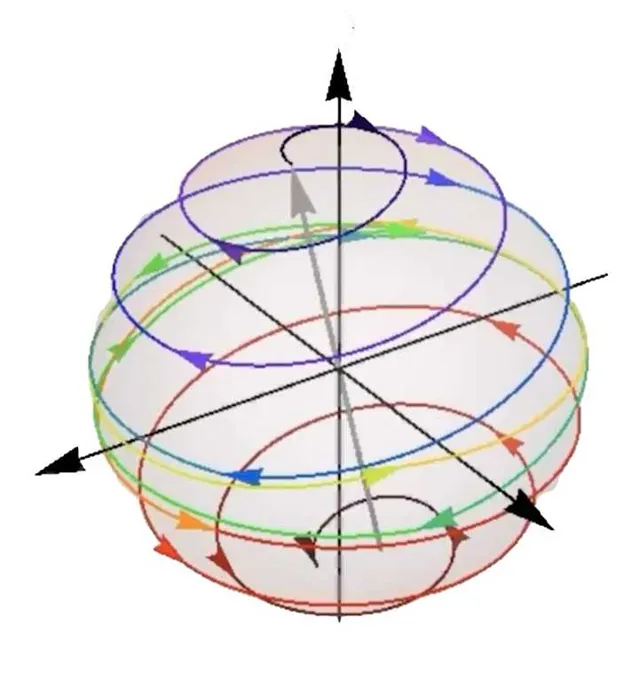
换而言之, 这里的构造相当于考虑两顶点分别为 |\psi_B\rangle 和 |\psi_{G}\rangle 的 Bloch 球面, 从顶点 |\psi_{B}\rangle 附近的球面上的点 |\psi_{\rm init}\rangle 出发, 在球面上环绕接近 |\psi_G\rangle , 并最终停留在 |\psi_{G}\rangle 附近. 这也就是为什么基于量子奇异值变换的构造能避免转过头 (即 overshooting) 的直观原因.
参考
- ^ a b Gilyén, András, Yuan Su, Guang Hao Low, and Nathan Wiebe. "Quantum singular value transformation and beyond: exponential improvements for quantum matrix arithmetics." In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, pp. 193-204. 2019.
- ^ a b Brassard, Gilles, and Peter Hoyer. "An exact quantum polynomial-time algorithm for Simon's problem." In Proceedings of the Fifth Israeli Symposium on Theory of Computing and Systems, pp. 12-23. IEEE, 1997.
- ^ a b Low, Guang Hao, and Isaac L. Chuang. "Optimal Hamiltonian simulation by quantum signal processing." Physical review letters 118, no. 1 (2017): 010501.
- ^ Yoder, Theodore J., Guang Hao Low, and Isaac L. Chuang. "Fixed-point quantum search with an optimal number of queries." Physical review letters 113, no. 21 (2014): 210501.
- ^ 准确地说, Grover 算法给出了 OR 函数的查询复杂度上界, 而 Brassard 和 Hoyer 的工作则是为了在一些情形下给出精确振幅放大 (exact amplitude amplification).
- ^ Regev 的讲义中有很清晰地表述: Regev, O. "Witness-preserving QMA amplification." Quantum Computation Lecture notes, Spring (2006).
- ^ Marriott, Chris, and John Watrous. "Quantum arthur–merlin games." computational complexity 14, no. 2 (2005): 122-152.
- ^ Watrous, John. "Zero-knowledge against quantum attacks." SIAM Journal on Computing 39, no. 1 (2009): 25-58.
- ^ Martyn, John M., Zane M. Rossi, Andrew K. Tan, and Isaac L. Chuang. "A grand unification of quantum algorithms." arXiv preprint arXiv:2105.02859 (2021).











