高斯在 数论(Number Theory) 中有着极其伟大的地位,那我们来聊一聊高斯在 虚数 i (Imaginary Number) 里的了不起的贡献。
正好最近阅读了一些有关虚数 i 的问题,得到了许多知乎大佬的启发. 发现自己之前回答的对于虚数的理解,有失偏颇,故此分享些自己对虚数在数论中的拙见.
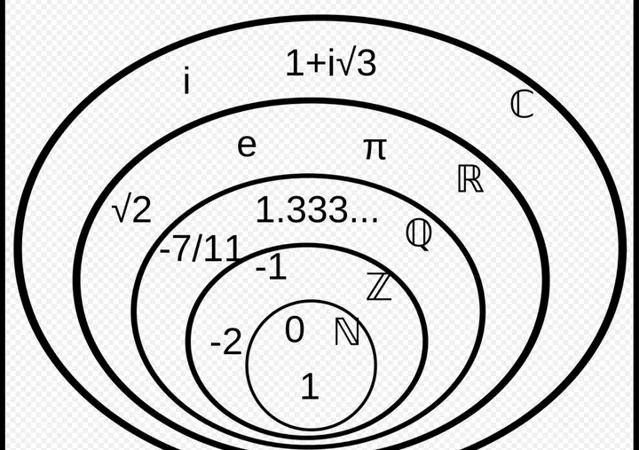
自从我回答了如何更形象地理解虚数 i 后,有小朋友会自然地发问:「为什么会创造虚数i=\sqrt{-1} 呢?是我们现有的数不够用了嘛?」很聪明喔!确实是不够用了. 复数(complex number) z=a+bi 的引入是为了解决更多的方程式. 事实上,我们曾为了解决方程 3x-7=0 ,引入了 分数 的概念,故有 x=\frac{7}{3} . 我们需要引入 负数 才能够解决 x+9=0 . 对于方程 x^{2}-2=0 ,我们需要引入 无理数 的概念,故解得 \pm\sqrt{2} . 但是我们还是无法解决方程 x^{2}+1=0 ,因为这个方程在实数中没有解. 所以我们自然会去 发明 * 新的数,从而去给出一个解.
* (尽管目前仍有不少数学家在争论虚数 i 是发明还是发现,正如大家经常议论「 数学是被发现的还是被创造的 」,这些问题是引人入胜的哲学难题(就像大多数优秀的哲学问题一样),它不太可能有一个明确的答案.)
那为什么我们只需要引入一个虚数 i 呢?难道不再需要其他的虚数吗?现在我们已经有 i=\sqrt{-1} 的概念了,可以去解决更复杂的方程了,例如 (3+2i)x^{3}-(\sqrt{3}-5i)x^{2}-(\sqrt[7]{5}+\sqrt[3]{14}i)x+17-8i=0 .
如果这个方程在我们的认知范围内没有解,我们则需要继续创造更多的数字. 令人意外的是,这个方程的解还是复数的形式,
x_{1}=1.27609+0.72035i, x_{2}=0.03296-2.11802i, x_{3}=-1.67858-0.02264i .
事实上,我们有足够多的复数去表示任意一个方程的解,这便是
定理Ⅰ. 代数基本定理(The Fundamental Theorem of Algebra) 如果 a_{0},a_{1},a_{2},…,a_{d} 都是复数,并且 a_{0}\ne0,d\geq1 , 则 a_{0}x^{d}+a_{1}x^{d-1}+a_{2}x^{d-2}+…+a_{d-1}x+a_{d}=0 ,有一个解在复数域.
除此之外,我们再来看看复数的四则运算.复数相加减时,实部与虚部分别相加减,跟向量的加减法相同. 复数的乘法也同样简单,我们有 (a+bi)(c+di)=ac+adi+bci+bdi^{2}=(ac-bd)+(ad+bc)i .
对于复数的除法,我们用有理化它的分母,得到 \frac{a+bi}{c+di}=\frac{a+bi}{c+di}\cdot\frac{c-di}{c-di}=\frac{(ac+bd)+(-ad+bc)i}{c^{2}+d^{2}} .由此可见,它是封闭的,还是在复数域内.
在 数论(Number Theory) 中我们把形如 a+bi 且 a,b 均为整数的复数成为 高斯整数(Gaussian integers) . 高斯整数与之前我们在一年级学的整数有很多相同之处,而之前我们所认为的数轴上的整数是 b=0 时的高斯整数. 如果 a 和 b 是高斯整数,那么它俩之和 a+b ,它俩之差 a-b ,它俩之积 ab 都是高斯整数. 但是,两个高斯整数相除,不一定得到一个高斯整数. 例如 \frac{3+2i}{1-6i}=\frac{-9+20i}{37} 就不是一个高斯整数,但 \frac{16-11i}{3+2i}=2-5i 就是高斯整数.
现在我们来观察复数的 因子分解(factorization) ,例如 1238-1484i=(2+3i)^{3}\cdot(-1+4i)\cdot(3+i)^{2} . 对于一般的整数 600=2^{3}\cdot3\cdot5^{2} ,我们可以更近一步化简成高斯整数 600=-i\cdot(1+i)^{6}\cdot3\cdot(2+i)^{2}\cdot(2-i)^{2} .
我们知道任何一个一般的整数都可以被分解成若干个素数因子,例如 7=1\cdot7 ,但我们也可以分解为 7=(-1)\cdot(-1)\cdot7 ,甚至还可以分解为 7=(-1)\cdot(-1)\cdot(-1)\cdot(-1)\cdot1\cdot1\cdot1\cdot1\cdot7 , 然后我们会意识到,如果不断地添加1和-1,将会得到无穷多种分解方式. 那是什么使得1和-1如此得与众不同呢? 因为只有它们俩有 整数乘法逆元(integer multiplicative inverse) , 1\cdot1=1,(-1)\cdot(-1)=1 . 我们会发现如果整数 a 不是1或者-1,也就没有另一个整数 b 可以满足等式 ab=1 ,那 a 就不会有整数乘法逆元. 所以我们把1和-1叫做 单位元(units) . 那高斯整数中有 元素(element) 哪些是单位元呢?最先想起的是 i 本身,因为 i\cdot(-i)=1 , 这个等式同样说明了 -i 也是一个单位元. 所以我们会继续思考,除了 1,-1,i,-i 之外,是否还存在其他的单位元?
为了回答这个问题,我们先假设在高斯整数中存在另外的单位元 a+bi . 因为它是一个单位元,所有它一定有一个整数乘法逆元,使其乘积为1,故有 (a+bi)(c+di)=1 , 展开等式的左边,得到 ac-bd=1,ad+bc=0 , 因此我们想找到满足这两个等式的解 (a,b,c,d) .
1^{0} 如果 a=0 , 则有 -bd=1 , 所以 b=\pm1,a+bi=\pm i ;
2^{0} 如果 b=0 , 则有 ac=1 , 所以 a=\pm1,a+bi=\pm1 ;
3^{0} 前两种情况正好对应着我们已知的四个单位元,对于剩下两种情况,我们假定 a\ne0 , b\ne0 , 则有c=\frac{1+bd}{a}\Rightarrow ad+b(\frac{1+bd}{a})=0\Rightarrow\frac{a^{2}d+b+b^{2}d}{a}=0 , 因为a\ne0 , 因此必须满足等式 (a^{2}+b^{2})d=-b , 由此可知,a^{2}+b^{2} 需要整除 b ,但是 a^{2}+b^{2} 一定比 b 大,故该情况无解.
综上所述,我们便可以得到
定理Ⅱ. 高斯单位元定理(Gaussian Unit Theorem) : 高斯整数中只有四个单位元,分别是 1,-1,i,-i ,只有它们有高斯整数乘法逆元.
值得注意的是,高斯整数是复数域的一个 子群(subset) ,而且子群里所有元素的和,差以及乘积仍然在该子群中. 当然数轴上一般的整数亦有该性质. 在数学中,我们将拥有这个性质的集合称之为 环(ring) .
再回到高斯整数的因子分解,我们可能会觉得如果一个高斯整数 \alpha 是一个素数,当且仅当只有 \pm1 和它本身能整除它. 但这样定义会造成一个问题,因为我们总是可以写出 \alpha=i\cdot (-i)\cdot\alpha ,因为任意的一个 \alpha 可以被 i,-i,i\alpha,-i\alpha 整除. 所以我们需要完善下最初的定义,便 有当且仅当高斯整数 \alpha 只能被 1,-1,i,-1,\alpha,-\alpha,i\alpha 和 -i\alpha 整除时,称 \alpha 为高斯素数(Gaussian prime). 换言之,只有单位元和 \alpha 乘单位元能整除 \alpha .

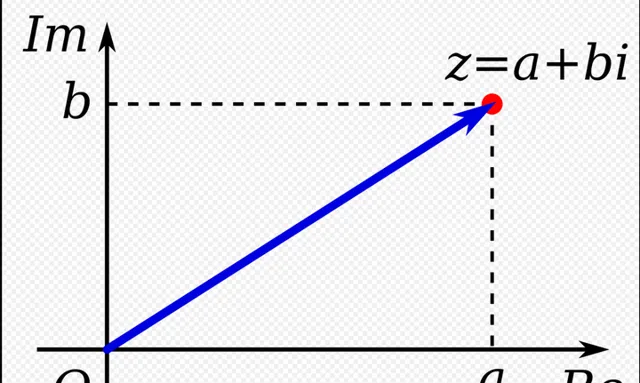
接下来我们就会探索,哪些数是高斯素数呢?举个例子,你认为以下哪些数字是高斯素数, 2,3,5,1+i,3+i,2+3i. 或许聪明的小朋友会根据刚刚的定义来判断,更简单的方法则是通过几何来确定. 例如平面内一点 (a,b) , 其中 a,b 为整数. 那么 (0,0) 到 (a,b) 的距离为 \sqrt{a^{2}+b^{2}} . 在数学中,我们用 范数(norm) 来刻画长度和大小的数学概念,所以我们定义(a,b) 的 范数(norm) 写作 N(a+bi)=a^{2}+b^{2} .
除此之外,范数在代数中有一条非常重要的性质:一个乘积的范数等于所有因子的范数之积. 因此我们就有
定理Ⅲ. (Norm Multiplication Property). 令 \alpha,\beta 为任意复数,则有 N(\alpha\beta)=N(\alpha)N(\beta) .
证明:令 \alpha=a+bi,\beta=c+di , 则有 \alpha\beta=(ac-bd)+(ad+bc)i , \alpha\beta 的范数为 (ac-bd)^{2}+(ad+bc)^{2} , \alpha 的范数和 \beta 的范数的乘积为 (a^{2}+b^{2})(c^{2}+d^{2}) . 因为 (ac-bd)^{2}+(ad+bc)^{2}=(a^{2}+b^{2})(c^{2}+d^{2}) ,故此定理成立.
在回到质因分解之前,我们不妨用范数去找单位元,或许能得到些新的启发. 假设 \alpha=a+bi 是一个单位元,这说明存在 \beta=c+di 使得 \alpha\beta=1 . 同时在等式两边取范数,得到 N(\alpha)N(\beta)=N(\alpha\beta)=N(1)=1 , 则有 (a^{2}+b^{2})(c^{2}+d^{2})=1 . 但是 a,b,c,d 均为整数,所有我们一定有 a^{2}+b^{2}=1 ,此等式的整数解只有 (a,b)=(1,0),(-1,0),(0,1),(0,-1) , 这就再次证明了高斯单位元只有 1,-1,i,-i 这四个数. 同时我们亦得到一个重要的性质, 当且仅当高斯整数 \alpha 的范数 N(\alpha)=1 , \alpha 为高斯整数单位元.
接下来让我们来尝试分解几个整数,例如2,令 (a+bi)(c+di)=2 , 等式两边同时取范数,得到 (a^{2}+b^{2})(c^{2}+d^{2})=4 ,
我们并不想让等式的左边出现单位元,显然, (a^{2}+ b^{2})=2,(c^{2}+d^{2})=2 .
如果我们取 (a,b)=(1,1) , c+di=\frac{2}{1+i}=\frac{2(1-i)}{2}=1-i . 因此 2=(1+i)(1-i) ,有两个其他的因子,所以2不是高斯素数.
用同样的方法检测3是否为高斯素数,最后得到 a^{2}+b^{2}=3,c^{2}+d^{2}=3 , 此时等式没有正整数解,因此3是一个高斯素数. 另外,5可以被分解为 5=(2+i)(2-i) , 所以5并不是高斯素数.
把以上的过程一般化,如果有一高斯整数 \alpha ,令 \alpha=(a+bi)(c+di) , 取范数得到 (a^{2}+b^{2})(c^{2}+d^{2})=N(\alpha) , 我们并不希望得到括号内的平方和等于1,因此我们要将范数 N(\alpha) 分解成 乘积AB 的形式,其中 A\ne1,B\ne1 . (以后我会写一篇哪些数可以写成两个平方数之和的文章)
还是先做几个简单的例子,我们分解 \alpha=3+i ,其范数为 N(\alpha)=10=2\cdot5 , 因此我们需要解决 a^{2}+b^{2}=2,c^{2}+d^{2}=5 . 这两个等式有多组解,比如 (a,b)=(1,1) , 可以得到 3+i=(1+i)(2-i) . 小朋友们可能想问,为什么会有多组解呢?因为我们可以用不同的单位元去分解 3+i . 因此当 (a,b)=(-1,1) 时,我们也可以得到 3+i=(-1+i)(-1-2i) . 其实第二种分解本质上跟第一种一样,因为我们有 -1+i=i(1+i),-1-2i=-i(2-i) .
再比如我们分解 \alpha=1+i , 其范数为 N(\alpha)=2 , 但 2 并不能被化简为 2=AB(A,B>1) 的形式,因为 2 本身就是数轴上的素数. 这说明\alpha=1+i 是一个高斯素数. 不失一般性,如果 N(\alpha) 是一个素数,那么 \alpha 就一定是一个高斯素数. 但这个性质也只说明了部分的高斯素数,比如 3,N(3)=9 ,这既是数轴上的素数亦是高斯素数. 接下来的定理便是此篇文章的压轴戏,完整地揭示了满足高斯素数的所有形式.
定理Ⅳ. 高斯素数定理(Gaussian Prime Theorem)
任何一个高斯素数可以被写为以下三种形式之一:
(i) 1+i 是一个高斯素数.
(ii)如果 p 是数轴上的素数且 p\equiv3(mod 4) , 那么 p 一定是一个高斯素数.
(iii)如果 p 是数轴上的素数且 p\equiv1(mod 4) , 将 p 写成两个平方数之和, p=u^{2}+v^{2} , 则有 u+vi 是一个高斯素数.
任何一个高斯素数可写为定理(i)(ii)(iii)中高斯素数乘单位元( \pm1,\pm i )的形式.
说些题外话,大数学家们其实也是一群很可爱的人,喜欢给自己研究的数赋予各种各样的名字(虽然有些名字听起来离谱得很). 比如定理(i)中的高斯素数叫做 ramified ,定理(ii)叫做 inert ,定理(iii)叫做 split . 神奇之处就在于,它们还没有自己的中文名喔,莫不是叫做「分歧,惰性,裂开」?!
这个定理的证明要运用一些初等数论的知识,比如同余,二次剩余和勒让德二次互反律(笔者最爱的定理之一,会写几篇关于二次互反律的文章),还有平方数之和的素数的性质. 学习过数论的小朋友可以继续阅读以下的证明过程. 若只是感兴趣的同学,可以先跳过证明部分,等待笔者随后会分享的初等数论笔记,当你以后准备好的时候,再回来看看.
证明 :我们之前就观察到如果 N(\alpha) 是素数,那么 \alpha 就一定是高斯素数. 定理(i)中 1+i 的范数为 2 ,所以它是高斯素数. 同样的,定理(iii)中 u+vi 的范数为 u^{2}+v^{2}=p , 所以这类数均为高斯素数.
接下来我们检验定理(ii),令 \alpha=p , 其中 p 是 p\equiv3(mod 4) 这一类型的素数. 如果 \alpha 可以被分解为 (a+bi)(c+di)=\alpha , 取范数得到 (a^{2}+b^{2})(c^{2}+d^{2})=N(\alpha)=p^{2} , 所以我们就需要解决等式 a^{2}+b^{2}=p 和 c^{2}+d^{2}=p . 但我们知道可以写成两个平方和的素数当且仅当 p\equiv1(mod 4) ,而这里是 p\equiv3(mod 4) ,所以这两个等式无正整数组解,因此 p 不可被分解,故此为高斯素数.
现在我们已经证实了定理(i)(ii)(iii)中所描述的皆为高斯素数,接下来要做的就是证明每一个高斯素数都在这三种形式里面. 为了证明这一点,我们便要拿出一个更强大的工具——新的引理!
引理Ⅴ. 高斯可除性引理(Gaussian Divisibility Lemma)
令 \alpha=a+bi 是一个高斯整数,则有
(a)如果 2 可以整除 N(\alpha) ,那么 1+i 可以整除 \alpha ;
(b)令 \pi=p ,且 p 为定理Ⅳ(ii)中的素数,如果 p 可以作为素数整除 N(\alpha) ,那么 \pi 可以作为高斯素数整除 \alpha ;
(c)令 \pi=u+vi 为一个高斯素数且满足定理Ⅳ(iii),令 \bar{\pi}=u-vi ,( \bar{\pi} 通常表示为共轭复数conjugate complex number),如果 N(\pi)=p 可以作为素数整除 N(\alpha) , 那么 \pi,\bar{\pi} 中有一个可以作为高斯素数整除 N(\pi) .
引理Ⅴ证明 :(a) 我们有2 整除 N(\alpha)=a^{2}+b^{2} , 所以 a,b 要么是都为奇数,或者是都为偶数. 这说明 a+b 和 -a+b 都可以被 2 整除,因此 \frac{a+bi}{1+i}=\frac{(a+b)+(-a+b)i}{2} 是高斯整数,故 a+bi 可以被 1+i 整除.
(b)我们有 p\equiv3(mod 4) 并且 p 整除 a^{2}+b^{2} ,这说明 a^{2}+b^{2}\equiv0(modp)\Rightarrow a^{2}\equiv-b^{2}(modp) , 使用勒让德符号得到 \left(\frac{a}{p} \right)^{2}=\left( \frac{a^{2}}{p} \right)=\left(\frac{-b^{2}}{p}\right)=\left( \frac{-1}{p} \right)\left( \frac{b}{p}\right)^2 . 因为 p\equiv3(mod 4) ,根据二次互反律 \left( \frac{-1}{p}\right)=-1 ,我们可以得到 \left( \frac{a}{p} \right)^2=-\left( \frac{b}{p} \right)^2 , 但是似乎我们最后得到的是 1=-1 ,是哪里出了问题呢?因为勒让德符号 \left( \frac{a}{p} \right) 只针对 a,p 两数不能整除的情况. 从得到的矛盾来看,这意味着 a,b 必须同时满足被 p 整除的条件,所以 a=pa^{'},b=pb^{'} . 因此 \alpha=a+bi=p(a^{'}+b^{'}i) 被 p=\pi 整除.
(c) 我们有 p 整除 N(\alpha) ,则 a^{2}+b^{2}=N(\alpha)=pK , 对于一些整数 K\geq1 . 然后我们需要证明 \frac{\alpha}{\pi}=\frac{(au+bv)+(-av+bu)i}{p} 或 \frac{\alpha}{\bar{\pi}}=\frac{(au-bv)+(av+bu)i}{p} 是一个高斯整数.
首先我们可以观察到 (au+bv)(au-bv)=a^{2}u^{2}-b^{2}v^{2}=a^{2}u^{2}-b^{2}(p-u^{2}) =(a^{2}+b^{2})u^{2}-pb^{2}=pKu^{2}-pb^{2}
所以 p 可以整除 (au+bv) 或者 (au-bv) .
根据另一个与上述相似的计算,得到 (-av+bu)(av+bu)=pKu^{2}-pa^{2} ,
所以 p 可以整除 (-av+bu) 或 (av+bu) .
接下来就需要分情况讨论,分别是:
① p 可以整除 au+bv,-av+bu ;
② p 可以整除 au+bv,av+bu ;
③ p 可以整除 au-bv,-av+bu ;
④ p 可以整除 au-bv, av+bu ;
情况①很容易证明,因为它直接意味着 \frac{\alpha}{\pi} 是高斯整数,所以 \pi 整除 \alpha .
同理可证④,所以 \bar{\pi} 整除 \alpha .
然后我们验证②, 推导出 p 可以整除 (au+bv)b-(av+bu)a=(b^{2}-a^{2})v . 因为 p 不整除 v 但 p 整除 a^{2}+b^{2} ,
所以我们发现 p 同时整除 2a^{2}=(a^{2}+b^{2})-(b^{2}-a^{2}),2b^{2}=(a^{2}+b^{2})+(b^{2}-a^{2}) .
并且 p\ne2 ,我们最终推导出 p 同时整除 a,b ,且令 a=pa^{'},b=pb^{'} ,
则有 \alpha=a+bi=p(a^{'}+b^{'}i)=(u^{2}+v^{2})(a^{'}+b^{'}i)=\pi\bar{\pi}(a^{'}+b^{'}i) , 因此我们得到 \alpha 同时可被 \pi,\bar{\pi} 整除.
同理可证③,所以\alpha 同时可被 \pi,\bar{\pi} 整除.
重回定理Ⅳ的证明: 假设 \alpha=(a+bi) 是任意一个高斯素数,我们要做的就是证明 \alpha 一定是在定理Ⅳ的三种类型里. 因为我们知道 \alpha 不是单位元,所以N(\alpha)\ne1 ,至少存在一个素数可以整除N(\alpha) .
首先假设 p=2 ,引理Ⅴ(a)告诉我们1+i 可以整除 \alpha ,但是 \alpha 应为素数,所以这说明 \alpha 是单位元乘 1+i 的形式,故为定理Ⅳ(i)中的高斯素数;
再假设 p\equiv3(mod 4) ,引理Ⅴ(b)告诉我们p 可以整除 \alpha ,所以\alpha 是单位元乘 p 的形式,故为定理Ⅳ(ii)中的高斯素数;
最后假设 p\equiv1(mod 4) ,因此 p 可以写成两个平方数之和, p=u^{2}+v^{2} . 根据引理Ⅴ(c), \alpha 会被 u+vi 或者 u-vi 整除. 因此 \alpha 为单位元与 u+vi 或者 u-vi 的乘积. 特别地, a^{2}+b^{2}=u^{2}+v^{2}=p , 故 \alpha 为定理Ⅳ(iii)中的高斯素数.
以上我们便完整地说明了每个高斯素数都符合这三种形式的其中之一,完成 高斯素数定理 的证明.











