看了一圈居然沒人提這兩本神作:
1. Andrea Goldsmith-Wireless Communication
2. David Tse-Fundamentals of Wireless Communication
兩本都屬於讀完樊昌信之後的高階版本,第一本較全面,Goldsmith是如今站在通訊領域金字塔頂端的幾個人之一,基本上把實體層的方方面面都寫了一遍,也算是緊跟著技術的發展。最後甚至介紹了點網路層的東西。
第二本主要講MIMO,Tse是柏克萊大牛,也是本領域頂級專家,其導師就是Gallager,所以Tse的分量不用我說也清楚了。不要被本書題目騙了以為真的是基礎,其實內容非常深,沒有數理基礎會被虐的很慘。建議先讀完第一本再看第二本,都有中文版,但轉譯均有很多錯誤,尤其是第二本轉譯很難看,有條件最好讀英文版。
這兩本書讀完之後我最大的一點體會就是,一定要形成訊號空間與訊號向量分析的概念(其嚴格的數學基礎來自泛函分析,如果想要深入建議也看一點泛函),樊昌信的書太過初級,從來不強調這一點。讀完後你會發現,絕大多數通訊問題都能夠歸結為幾何問題,腦子裏形成幾何影像之後你就會發現很多通訊理論是如此簡潔美妙。
我這裏舉一個Tse書中講AWGN通道容量的例子(這一幾何影像最初應該是來自夏農那篇著名的論文Communication in the presence of noise),國內的消息理論教材一般都是從互資訊最大化的角度來推導容量的,這樣當然更為嚴格,但缺乏直觀意義。根據取樣定理,任何一個頻寬為B,時長為T的訊號,至少需要N=2BT個樣本才能重建,因此可以理解為訊號空間近似是N維的,任一接收訊號均可以表示為N維歐式空間中的一個點。那麽在這樣一個N維訊號空間裏,怎樣才能最大化頻譜效率?這裏就要參照Tse的名言:一個優秀的通訊方案應該利用通道中所有可用的自由度。
假設給定發送訊號功率約束P ,高斯白雜訊的變異數為\sigma ^{2} 。根據大數定律,N維接收向量將以很高機率位於半徑等於\sqrt{N(P+\sigma ^{2} ) } 的超球內,對於較大的N,接收向量同樣以較高機率位於發射星座點周圍半徑等於\sqrt{N} \sigma 的雜訊球表面附近。只要接收向量不相互重疊(亦即接收向量可以被區分開來)就可以進行可靠的通訊,因此不發生重疊的最大星座點數量就是大超球的體積與雜訊球體積之比:
\frac{\sqrt{N(P+\sigma ^{2} )} ^{N} }{\sqrt{N\sigma ^{2} }^{N} }
對上式取以2為底的log,就是在T時間內可以傳輸的最大位元數,再除以T,就可以得到最大速率:
\frac{1}{T} log(\frac{\sqrt{N(P+\sigma ^{2} )} ^{N} }{\sqrt{N\sigma ^{2} }^{N}}) =B log(1+\frac{P}{\sigma ^{2} } )
這就是AWGN通道的容量,相信這個解釋能夠讓人明白「容量」這個詞是怎麽來的。這一填球模型同樣可以形象地說明為什麽這個容量是極限值,因為雜訊球之間無論如何都會有縫隙,導致訊號空間不能被完全填滿。
下面這個從Tse的書裏截下來的圖可以說明問題:
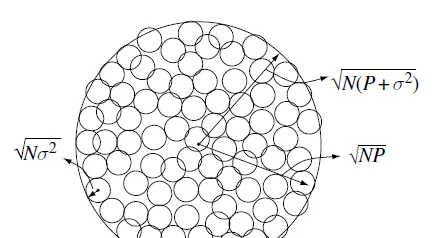
不覺得夏農公式實在是太美妙了麽?
值得一提的是,Tse和他的弟子Lizhong Zheng把夏農這套填球模型從歐式空間推廣到了非歐空間。在非相幹MIMO通訊(Non-coherent MIMO)中,發射機和接收機都不知道通道狀態資訊(CSI),此時能達到容量的碼字X是么正矩陣,假設通道矩陣H為良態的,在接收端,接收碼字為Y=HX+W,W為加性高白。高訊雜比條件下,由於H未知,Y可以理解為X行向量張成的線性子空間。這一子空間是Grassmann流形上的點,which suggests 接收向量位於Grassmann流形上,而不是在Rn中。不同於普通AWGN通道,在該場景下,歐式空間中的填球模型將轉化為Grassmann流形上的填球模型。Tse和Lizhong Zheng在2002年發表於IEEE Trans on Information Theory上的 "Communication on the Grassmann manifold: a geometric approach to the noncoherent multiple-antenna channel."一文給出了這一模型並求解了容量,該文被參照800余次,並獲得了IEEE Information Theory Society當年的Best Paper Award。現在業界很多人提起Lizhong Zheng和Tse的工作一般都只想到分集和復用折中(Diversity-multiplexing tradeoff ),而我個人更喜歡他們的這項工作,非常美妙,也是我最推崇的那種工科理論研究。
我個人的經驗是,讀教材要抓住一條主線,比如Tse的教材裏面freedom degree這個概念貫穿全書。讀這些書的時候不妨以「通訊系統的幾何表征」為主線,並思考如下一些問題,加深對通訊問題的幾何特性的理解:
1、線性濾波器的「線性」是什麽意思?其幾何依據是什麽?
2、把QAM訊號和MPSK訊號分成I/Q兩路的數學依據是什麽?
3、對線性調變的訊號進行解調時,解調器中的積分器存在的依據是什麽?其幾何解釋是什麽?
4、糾錯編碼的幾何解釋是什麽?為什麽可以減小誤碼率?
5、CDMA中非正交碼(如m序列)和正交碼(如沃爾什-哈達瑪碼)相比有什麽好處?
...等等等等。
這些都是通訊過程中的基本概念,其幾何解釋是十分簡潔的。可惜這些內容都是我讀博士的時候自己看書和思索想到的,本科的時候通訊原理老師從來都沒有這樣和我們講過,再加上本科不好好學習,專業知識都沒學到多少,現在不得不自己補課。以上這些東西我也沒有完全搞明白,還在慢慢研究。
希望對你有幫助。











