LQR(Linear Quadratic Regulator)即線性二次調節器,作為一種最優控制器,透過設計出的狀態反饋控制器K使得二次型目標函式J取得最小值,從而達到最優控制的目的。本篇以Apollo源碼例項闡述LQR在車輛橫向控制中的套用,從仿真到實作分析該演算法的控制效能。
程式碼連結:
對於車輛的橫向系統,不難得知基於跟蹤誤差變量的狀態方程式模型為:
\scriptsize \frac{d}{dt}\begin{bmatrix}e_1 \\ \dot{e_1} \\ e_2 \\ \dot{e_2} \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0\\ 0 & -\frac{C_{af}+C_{ar}}{mV_x} & \frac{C_{af}+C_{ar}}{m} & -\frac{C_{af}l_{f}-C_{ar}l_{r}}{mV_x} \\ 0 & 0 & 0 & 1\\ 0 & -\frac{C_{af}l_{f}-C_{ar}l_r}{I_zV_x} & \frac{C_{af}l_{f}-C_{ar}l_r}{I_z} & -\frac{C_{af}l_{f}^2-C_{ar}l_r^2}{I_zV_x} \end{bmatrix} \begin{bmatrix}e_1 \\ \dot{e_1} \\ e_2 \\ \dot{e_2} \end{bmatrix}
\scriptsize + \begin{bmatrix} 0\\ \frac{C_{af}}{m}\\ 0\\ \frac{C_{af}l_f}{I_z} \end{bmatrix}\sigma + \begin{bmatrix} 0\\ -\frac{2C_{af}l_{f}-2C_{ar}l_r}{mV_x}-V_x\\ 0\\ -\frac{2C_{af}l_{f}^2+2C_{ar}l_r^2}{I_zV_x} \end{bmatrix}\dot{\varphi _{des}}
其中, \scriptsize e_1 為橫向偏差, \scriptsize e_2 為航向角偏差,上述模型可參照< 車輛動力學及控制 >第二章;
由此,可將其重寫為:
\scriptsize \dot{x} = Ax+Bu+C
由於上述系統為連續系統,還需進行相應的離散化。離散化後,對應的標準形式為:
\scriptsize x(k+1)=A_d*x(k)+B_d*u+C_d
各變量的對應關系如下:
\scriptsize A_d = \frac{e^{\frac{AT}{2}}}{-e^{\frac{AT}{2}}} = \frac{I+\frac{AT}{2}}{I-\frac{AT}{2}} =({I-\frac{AT}{2}})^{-1}(I+\frac{AT}{2})
\scriptsize B_d = \int_{T}^{0}e^{AT}dtB=TB
\scriptsize C_d=TC
目標函式的選擇:
\scriptsize J=\sum_{N-1}^{0}(x^TQx+u^TRu)
其中 \scriptsize Q 為狀態權重矩陣, \scriptsize R 為控制權重矩陣, \scriptsize x 為狀態矩陣, \scriptsize u 為控制矩陣。
基於LQR的橫向動力學仿真效能分析
由橫向動力學方程式可知,不同車速情況下,其動力學表征不同。為分析車速對控制效能的影響,特構建Matlab的效能仿真環境,以此來分析工況的不同對控制效能的影響。
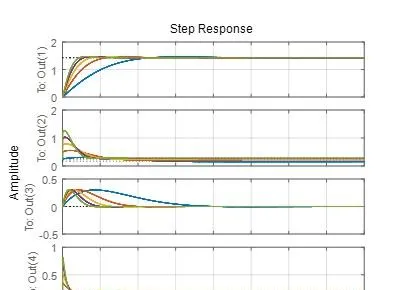
階躍響應分析:不同車速下,系統的單位階躍響應曲線如圖所示。由圖可知,當輸入的速度越快時,系統的響應越快。
魯棒效能分析:
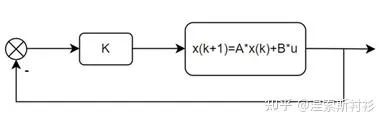
LQR的系統框圖可知,橫向系統的開環增益函式:
\scriptsize L(s)=K(SI-A)^{-1}B
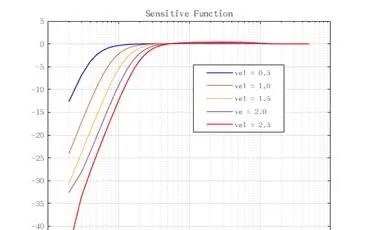
由此,靈敏度函式可寫為:
\scriptsize S = \frac{1}{1+L(s)}
由靈敏度函式的響應特性可知,系統在低速狀態下的誤差抑制效能相對較弱。
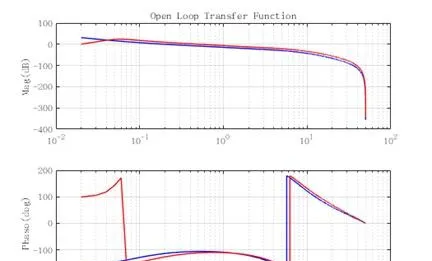
為改善系統的響應特性,Apollo還引入了Lead_Lag控制器。當引入Lead_lag控制器後,系統的開環幅頻響應特性為:
MPC與LQR的比較:
(1) LQR的研究物件是現代控制理論中以狀態空間方程式形式給出的線性系統,而MPC的研究物件可以是線性系統,也可以是非線性系統。不過對於非線性系統,可以將其線性化處理後進行求解。
(2) 本質上都屬於最佳化問題;
(3) 工作時域的不同,LQR的計算針對同一工作時域,在一個控制周期內,LQR只計算一次,並將此次計算出的最優解下發給控制器即可;而MPC是捲動最佳化的,計算未來一段時間內,每個采樣周期都會經過計算,得出一組控制序列,但是只將第一個控制值下發給控制器.
參考文獻
[1] 自動駕駛(七十二)---------LQR控制演算法
[2] LQR and MPC
[3] 開發者說 | Apollo控制演算法之汽車動力學模型和LQR控制
未完待續











