等價關系有什麽意義？等價關系說明了什麽問題？

在考慮等價關系、相容關系、偏序關系之前，我們需要對關系的關鍵性質做一個感性、直觀的理解。離散數學裏面的這些形式化的定義，和生活更是緊密相關啦，在電腦領域會大量用於問題建模。

註意，我們討論的關系，都是在某個集合（比如A）上的關系，即二元組的兩項都屬於A。下面用R指示關系，用A指示關系所在集合。

關系的五種性質

自反性與反自反性：是否每個元素與其本身構成關系？還是每個元素與自己都沒有關系？

對稱性與反對稱性：關系是否是完全雙向的？是否是絕對單向的？在後面，配合傳遞性，對稱性自然引出了等價關系，反對稱性引出了偏序關系。

傳遞性：傳遞性意味著關系的扁平化，在「距離」上的invariance。

1. 從關系圖的視角看，從任何一個點走兩步都不會抵達新的位置，也意味著，任何能到達的位置都可以一步到達（扁平化的意味）；
2. 體現在關系矩陣上，它（在邏輯上）呈現一種上/下三角的狀態，比如a->b->c的關系矩陣——對於一個傳遞性的關系，其中任意一個「傳遞鏈條」，都呈現上/下三角的樣態【註意，是可以透過對完整的關系矩陣進行初等變換後，可以使這一個鏈條所對應部份成為上/下三角的樣態】。

傳遞性由合成運算而來。我們也一起重新回顧一下。

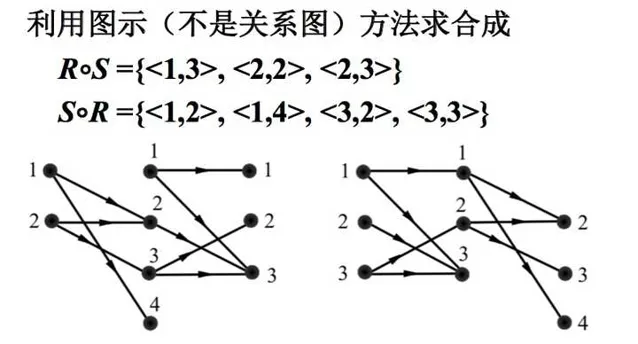
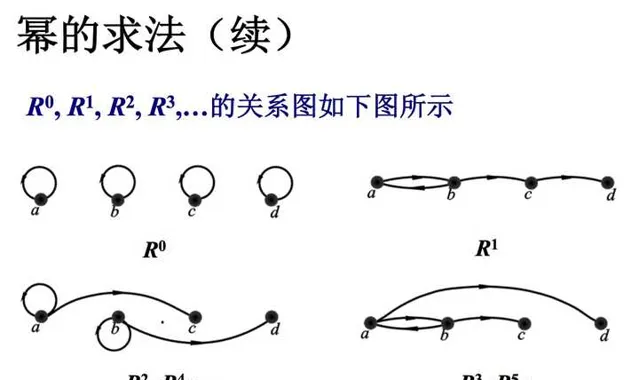
從哈斯圖中看傳遞性的意義：我們不再關註任意兩元素中間有多少個結點。

對五種性質理解的強化

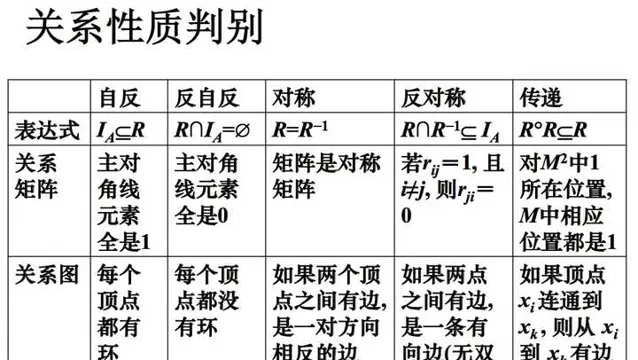
1. 五種性質的充要條件是什麽？

2. 如何判別這五種性質？

3. 如何證明某個關系符合性質？

4. 運算與性質的關系——運算維持相應性質嗎？為什麽？此處可以進一步深化直觀理解。

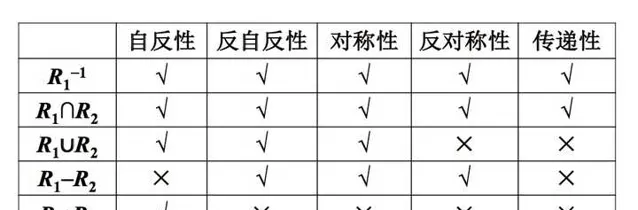
我對不再保持的性質做簡單的自己的解讀。

集合的差不再保持自反性：對角線都被剪掉了嘛。

集合的合成不再保持反自反性：扁平化後，自己就算是指向自己了。

集合的合成不再保持對稱性：對接處可能未連線上，如{<1,3><3,1>}與{<2,3>,<3,2>}，是二元組的順序帶來的。

集合的聯集不再保持反對稱性：可能兩者直接互補了嘛。交集為何可以？因為一定會更小。

集合的合成不再保持反對稱性：看傳遞矩陣，反自反性的單向性是一個非常弱的約束，R2可以對R1做任意的調整，讓某個元素指回自己。【這裏有些詞不達意。可以自己畫畫計算集合合成的那張圖】

到了傳遞性：為何交運算保持？三角與三角的交集還是三角；並運算不保持？三角與三角的聯集會缺一個角，環通度僅部份地被擴張了；合成也不行？和並運算類似嘛。

5. 閉包的構造：為何傳遞閉包要比對稱閉包後算？: -）對稱閉包讓所有關系都變成了雙向，比如 a->b->c與d->b->c，a與d是沒關系的，所有關系右多了個反向，他倆就應該有關系了。

等價關系、相容關系、偏序關系

1. 等價關系：自反 + 對稱 + 傳遞

若說傳遞性的扁平化還沒有消除關系的方向性，那麽它與對稱性的配合就徹底的讓關系變成了零維的，完全失去了階級性（偏序還保持這一點）。之前說，傳遞性可以理解為上/下三角，那麽配合對稱（以及比較trivial的自反性，它就是對角線），那麽就是個正方形了。正方形意味著，其內部關系的完整性，以及與其他元素的隔離性。而對於等價關系，它的關系矩陣一定可以轉換為只在其對角線圍繞著一串正方形的形式。

在等價關系中，一個等價類不分階級、不同等價類不可比較。

應該很好理解了。商集，就是所有等價類的集合；劃分，就是所有等價類擺在一起；塊數，就是劃分的秩。

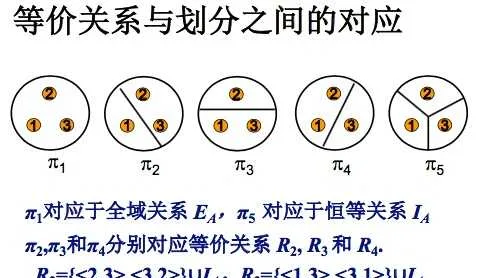
我們如何求一個劃分呢？根據問題中的等價條件，抽象出等價的形式定義就好啦。

總結：等價關系是一種條件極其強大（簡單）的關系，它完全消解的關系運算中的invariant，完全扁平化。

2. 相容關系：自反 + 對稱

朋友的朋友不一定是朋友，但也很有可能是朋友，朋友關系就是相容關系的一個很好例子。相容關系中，最主要的就是「對稱性」，也就是雙向性，是相容的意味。相容關系消解了方向性。

一個朋友圈，就是一個相容類（主要是「最大相容類」概念）：這個圈子內的人彼此都是朋友，這是類似等價類的概念。但一個人可以處於多個圈子內，這是與等價類不同處。

我們想象一個N個人的完整的社交圈：那就是要看這些人的朋友關系的 完全覆蓋 ，即所有最大相容類的集合。再申，一個人可以出現在多個最大相容類中，這是與等價關系的差異。

3. 偏序關系：自反 + 反對稱 + 傳遞

還用三角的比喻，偏序關系就是帶對角線的三角，且不允許出現邊長大於1的正方形。

兩個元素可比，意味著在同一個三角形上（還是邏輯上的三角形，可能需要堆關系矩陣經過變換得到）。全序，則是一個巨大的三角形。

覆蓋關系，用於找到在偏序集上最緊湊的（相鄰的）兩個元素，用於後面畫哈斯圖。由於偏序關系有方向，還是保持著某種「距離」的含義，但它對這個關系本身無任何內涵上的聯系，只是用來畫圖而已。

偏序集：集合 + 偏序運算。

哈斯圖：就是很像樹的圖，「父子」的關系是覆蓋。哈斯圖中可能有許多樹。每棵樹可以有許多樹根【極小元】。每棵樹可以倒過來，看起來還是一棵樹。上下界、上下確界，存在性也就很顯然啦。無限，也就可能無界，正如因果鏈，有沒有第一因呢！對於無限集合，確界，也可能在關系的定義域之外，類似開區間與其邊界的關系。