謝邀,這是非常典型的 約瑟夫問題 (Josephus problem)的一個變體。
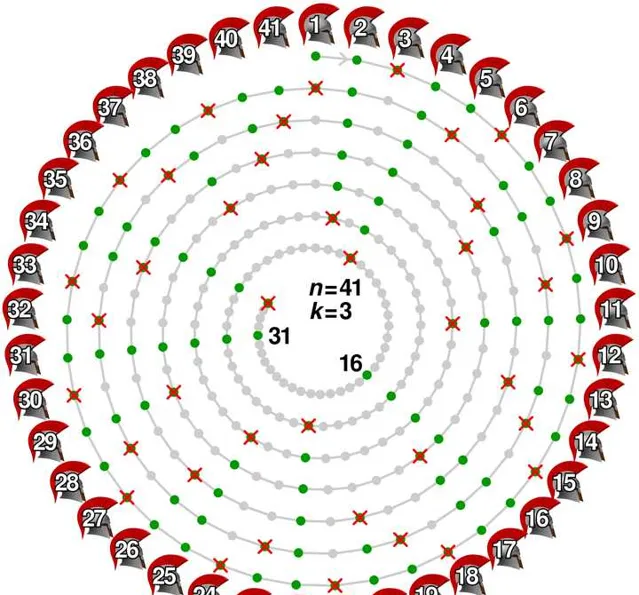
約瑟夫問題指的是,所有的人站成一圈等待處決,從圓圈中指定位置開始,並沿指定方向圍繞圓圈進行。 在跳過指定數量的人之後,處刑下一個人。剩下的人按照此流程重復進行,問最後活下來的是誰?
具體地,如上圖所示,總共 n=41 個人站成一圈等待處決,每隔 k-1=3-1=2 個人就進行處決。圖中顯示最後被殺死的是第 16 號和第 31 號士兵。
回到題主的問題,題主相當於是把約瑟夫問題中的 確定性處決 更改為 機率性處決 ,且指定了 相鄰 的人進行機率性處決(即 1 號對 2 號開槍,2 號對 3 號開槍,……,100 號對 1 號開槍)。
對於誰是最有可能活下來的人,嚴格計算應該是可以的,但我目前還沒找到好的解決辦法。
補充一句:我看其他答主的回答似乎都是假設了每次開槍都會重設彈倉,但和(我個人理解的)題意不同。我的程式碼模擬的是, 開槍後不重設彈倉,直接交給下一個人進行射擊,直到有人中彈後才重設彈倉 。為了保護發際線,數值模擬更加解憂省事。
更新: @皮皮蝦-9527 已經給出了完整解答,具體請見回答:圓桌上 100 個人輪流開槍,最可能活下來的是幾號?我們可以透過編程來模擬一下結果:
import
random
import
matplotlib.pyplot
as
plt
def
game_simulation
(
num_players
=
100
,
num_simulations
=
1000000
):
survivor_counts
=
[
0
]
*
num_players
for
_
in
range
(
num_simulations
):
players
=
list
(
range
(
1
,
num_players
+
1
))
# players = [1, 2, ..., 100]
bullet_position
=
random
.
randint
(
1
,
6
)
# 隨機初始化子彈位置
current_position
=
0
# 從 1 號玩家開始持槍
while
len
(
players
)
>
1
:
if
bullet_position
==
1
:
# 當前持槍玩家的下一位玩家中彈,將其移出遊戲
players
.
pop
((
current_position
+
1
)
%
len
(
players
))
# 重設子彈位置
bullet_position
=
random
.
randint
(
1
,
6
)
# 當前持槍玩家調整為中彈玩家的下一位玩家
if
current_position
==
len
(
players
):
current_position
=
0
else
:
current_position
=
(
current_position
+
1
)
%
len
(
players
)
else
:
# 子彈未發射,輪到下一位玩家
bullet_position
-=
1
current_position
=
(
current_position
+
1
)
%
len
(
players
)
# 記錄最後幸存者
survivor_counts
[
players
[
0
]
-
1
]
+=
1
# 找到幸存次數最多的玩家
most_likely_survivor
=
survivor_counts
.
index
(
max
(
survivor_counts
))
+
1
# 找到幸存次數最少的玩家
most_likely_death
=
survivor_counts
.
index
(
min
(
survivor_counts
))
+
1
return
most_likely_survivor
,
most_likely_death
,
survivor_counts
most_likely_survivor
,
most_likely_death
,
survivor_counts
=
game_simulation
()
print
(
f
"最可能的幸存者是第
{most_likely_survivor}
號玩家。"
)
print
(
f
"最可能的倒黴蛋是第
{most_likely_death}
號玩家。"
)
print
(
"每位玩家的幸存次數:"
,
survivor_counts
)
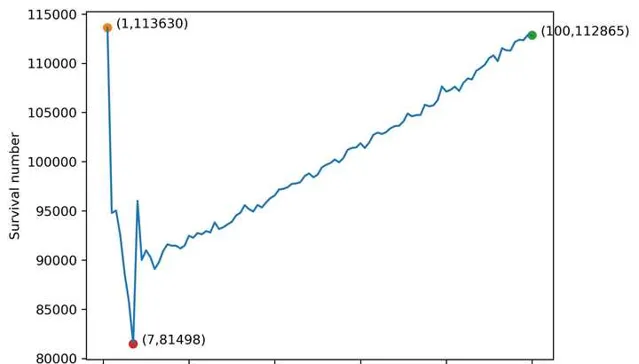
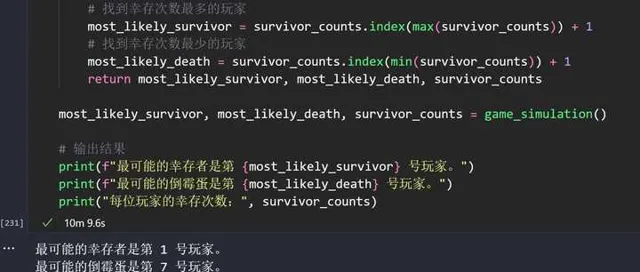
執行 1000 萬次的遊戲模擬後,我們發現 最可能的幸存者是 1 號玩家 。(但並不絕對,1 號玩家的幸存次數和 90 ~ 100 號玩家的幸存次數差別不是很大)
但明顯可以看出來的是, 最容易去世的是 7 號玩家。
>> 最可能的幸存者是第 1 號玩家。>> 最可能的倒黴蛋是第 7 號玩家。
>> 每位玩家的幸存次數: [113630, 94789, 95030, 92461, 88633, 85760, 81498, 96017, 90016, 90987, 90308, 89092, 89777, 90939, 91599, 91456, 91454, 91178, 91471, 92468, 92262, 92744, 92615, 92942, 92805, 93829, 93155, 93328, 93632, 93885, 94538, 94805, 95580, 95169, 94934, 95600, 95341, 95850, 96303, 96567, 97172, 97231, 97397, 97749, 97779, 97928, 98534, 98804, 98414, 98670, 99422, 99679, 99868, 100214, 99931, 100356, 101199, 101392, 101445, 101877, 101390, 101925, 102725, 102952, 102808, 103007, 103395, 103609, 103653, 104075, 104891, 104607, 104732, 104745, 105786, 105626, 105711, 106266, 107642, 107120, 107291, 107625, 107181, 108014, 108448, 108361, 109235, 109511, 109860, 110527, 110796, 110211, 111535, 111316, 111295, 112155, 112389, 112346, 112866, 112865]
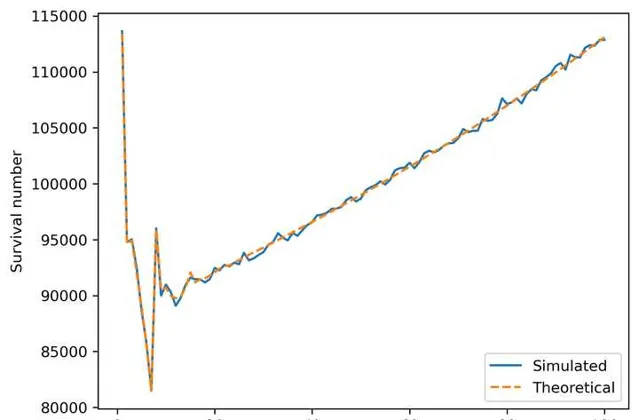
有一個猜測角度是,2 號玩家的幸存率應該 約等於 1 號玩家的 5/6。理由如下:
在我們的 1000 萬次模擬中,2 號玩家幸存次數與 1 號玩家幸存次數之比是 \dfrac{94789}{113630} \approx 0.83\approx \dfrac{5}{6} ,這也符合預期。
根據 @皮皮蝦-9527 的解析結果,2 號玩家幸存機率與 1 號玩家幸存機率之比是 0.83452\cdots\approx \dfrac{5}{6} ,這與上述論斷一致(說明我們的猜測是合理的)。









