省流版本:在100000次的模擬中,100,78,95名列前三;分別存活了1097,1093,1089次,最大存活率在1.1%左右;27,18和12最危險,都只存活了868,903和909次。
如下圖所示,其中藍色線段為100000次的模擬數據,黃色線段為 @張雄騏 大佬的解析解的結果,我們可以看出二者是十分吻合的 [1] 。解析解指出1號將具有最大的生存率,實際上如果我們把1號視作最後接受槍擊的101號的話,我們也能自然地看出『 序號越大後生存機率越大 』的特點。
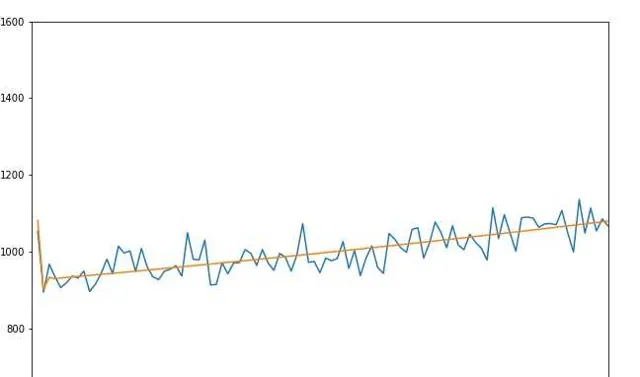
經典的約瑟夫問題的變形,引入了左輪賭局這個隨機變量。我們這裏假設每次開槍意味著有六分之一的機率死亡,那麽我們就可以先模擬一下。
首先,我們先生成一個標準的 迴圈連結串列 。

class Node(object):
def __init__(self, value):
self.value = value
self.next = None
def create_linkList(n):
head = Node(1)
pre = head
for i in range(2, n+1):
newNode = Node(i)
pre.next= newNode
pre = newNode
pre.next = head
return head
如果開槍成功,我們就將當前Node從 迴圈連結串列 中移出,直到整個迴圈連結串列中只剩下一個Node時遊戲結束。
def test():
head = create_linkList(100)
pre = None
cur = head
while cur.next != cur:
pre = cur
cur = cur.next
# 引入判定條件
if randint(1,6) == 1:
pre.next = cur.next
cur.next = None
cur = pre.next
return cur.value
之後我們再模擬10000次,再排序就出現結果了。

然後是上述模擬程式的可能的誤差來源。
首先是用於生成隨機數
randint
函式,此函式的隨機性由Mersenne Twister演算法保證,理論上的隨機數周期為 2^{19937}-1
,以目前的迴圈次數來看,還是
不需要考慮因隨機數迴圈導致的取樣偏差的
。
評論區中給出了另外一種理解題意的方式,即『 若槍未發射,則繼續傳遞,所以下一發射出的機率應該增加 』。從個人角度來說,我認為這兩種情況在統計結果上應該是等價的。就類似與開獎先後的順序實際上不會影響獲獎機率的。
update
上述解法給出的是『每位都有六分之一的機率死亡』的模擬,這一點和題目中所謂的『傳遞手槍』的說明並不完全相同。以下給出『 傳遞手槍 』的解法:
def test_same_gun(n):
head = create_linkList(n)
pre = None
cur = head
bullet_pos = randint(1,6)
while cur.next != cur:
# 傳遞手槍
for _ in range(bullet_pos):
pre = cur
cur = cur.next
bullet_pos = randint(1,6)
pre.next = cur.next
cur.next = None
cur = pre.next
return cur.value
可以料想,『傳遞手槍』實際上相當於給所有人分組了,比如2-7號,其中必定至少會有一人被射擊。
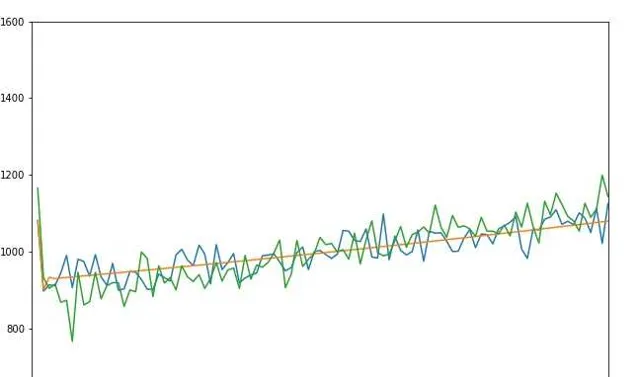
參考
- ^https://www.zhihu.com/question/8225556361/answer/67650588974










