之前鼓起勇气写了下面这篇文章。贴出来应该可以回答这个问题,供参考^_^。
简谐振动是最简单最基本的振动,它的典型例子是弹簧振子。
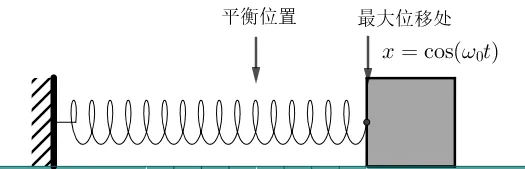
什么是弹簧振子呢?一个不考虑质量的弹簧连接一个有质量的小球或物块,然后把它沿着弹簧的方向压缩或者拉伸一定的距离(不要拉得太狠,悠着点儿)后松手,那么物块就会 只在弹簧弹力的作用下,周期性地往复振动 。弹簧振子是一个理想物理模型。振子速度最大的位置回复力为零,此处称之为 平衡位置 。
在高中我们就知道,弹簧振子的运动学方程可以表达为如下正弦或余弦函数形式:
\begin{aligned} x(t)=A \cos (\omega t+\varphi)\\ x(t)=A \sin (\omega t+\varphi’) \end{aligned}\\
它们都表述了 振子偏离平衡位置的位移随时间变化的关系 。由中学数学可知这两个函数是等价的。 那么这个振动方程到底是怎么推导出来的呢?
我的书架上有四本书对这个振动方程有所描述,分别是漆安慎版【力学】、人教社的高中物理教材、【费曼物理学讲义】、赵凯华版【新概念物理教程·力学】,外加知乎@烤羚羊的思路。他们 面对同一件事虽然思路迥异,却又殊途同归,真真是各有各的特点,各有各的巧妙 。我们一起来看看吧^_^
方式一 「易得」型
这种方式的典型代表是漆老的【力学】,在书中,振动方程来自于直接写出微分方程的解,画风是下面这这样的:

为什么可以写成这样呢?当时的我左思右想也没搞明白这个余弦函数是怎么来的。漆老可能觉得读者基本都是大学生了,这等小菜,自己可以推出来。看来我和漆老对大学生的基本要求隔了一个地球周长。所以当时我只是把它当成基本结论去记的。现在,这种处理方式着实不能满足我对科学的渴望,必须深究下去。
方式二 科学探究型
这种方式的典型代表是现行高中物理人教版教材。从国家到地方都在大力开展新课程改革,要求在物理教学中要重视学生的物理探究过程, 多多体验一下科学家们发现问题、提出猜想、设计实验、得出结论、讨论验证等的科学研究过程 。所以人教版高中物理教材是按如下方式得出振动方程的。
首先, 观察弹簧振子的频闪照片 。
让弹簧振子先振动起来,然后让频闪仪对着弹簧振子每隔 0.05s闪光一次,闪光的瞬间振子就会被照亮,从而得到闪光时小球的位置,相邻两个位置之间的时间相隔为0.05 s。拍摄时让底片从左向右匀速运动,因此在底片上留下了小球和弹簧的一系列的像。

或者,在桌面上放一个弹簧振子(附一支描线笔),下面放上一条长长的宽纸带,然后在弹簧振子振动的同时在一侧把纸带匀速卷起来,这样就得到一条和频闪照片类似的图像。
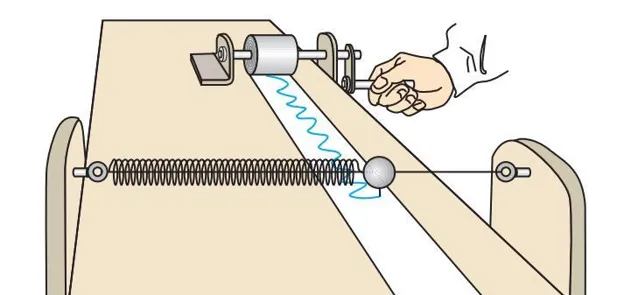
然后, 猜想图像的函数并验证 。书上引导读者猜想这是正弦函数。然后根据振幅和周期写出正弦函数表达式,再从实验中得到的图像中选择几个点,得到不同时间所得到的位置值,把这个位置值和表达式中对应时间的函数值做个比较。如果符合得很好,说明振动图像就是对应正弦函数。
接着,书上就直接给出了振动方程,如下图所示。

人教版高中教材的这个方法简单直观,规避了严谨的数学推理。其中,把时间作为一个数轴,位移作为另一个数轴,从一维振动中拉一个二维图像的方法是很奇妙的一个思路。
然而,弹簧振子的一维振动,怎么就跟三角函数扯上了关系呢? 弹簧振子难道就有没有什么内在的、固有性质使得它必然与三角函数有关系吗?
答案显示不是。 一定是弹簧振子的某些固有属性使得它与三角函数有关系 。那么我们首先就得找找,弹簧振子到底有哪些固有的属性和规律呢。
弹簧振子的常微分方程
(如果你时中学生,当你看到常微分方程这五个字时也许会比较纳闷,先不管它,我们来一步步把它给逼出来)
弹簧振子的固有属性
弹簧振子有哪些固有属性会影响到它的振动呢?
首先要想到的性质一定有 物块的质量 m ,我们可以想想,在弹簧被拉伸的长度一定的前提下,如果物块越重,那么振子就应该越「懒」,运动状态越难得改变,也就是振动得越慢。所以质量m 可能会在振动方程中体现出来。
接着,我们还应该想到弹簧的 劲度系数 k 也会影响到振动的快慢。如果弹簧越是「硬邦邦」,在弹簧被拉长相同的长度时所具有的拉力越大,物块受到更大的拉力应该会更快地回到平衡位置。所以劲度系数k 也可能会在振动方程中体现出来。
有了质量和劲度系数,这只是我们寻找振动方程的一小步,还需要从弹簧振子必须满足的内在规律上找。
振子的牛顿第二定律
最先想到的应该是牛顿运动定律。
中学时老师就讲,牛顿牛爵爷把力和运动通过 牛顿第二定律 结合起来,小到灰尘,大到天体都可以用它,可以说是相当的厉害。弹簧振子自然也不例外。也就是说,弹簧振子一定满足F=ma ,其中,F 就是弹簧受到的弹力,a 是振子的加速度。
但是,这和我们寻找的振动方程有什么关系呢?牛二定律里面并没有出现时间、也没有出现位移呀。其实,这里需要一丢丢的微积分知识,利用微积分, 加速度可以表达为位置矢量的二阶导数 。即可以把牛顿第二定律表达为如下形式:
F= ma = m \frac{\mathrm{d} ^{2}x}{\mathrm{d}{t^2}} \\
如果你没有微积分方面的数学储备,推荐你参阅长尾科技的文章【你也能懂的微积分】。
这样一操作,x 和t 就立马出现了,似乎答案以经找到了。仔细一想,其实还没有。你想想看,在振子振动的过程中,弹力总是保持不变的吗?显然不是。换句话说, 弹力 F 也会随着时间,或者说随着位移发生变化 。如果力F 不随位移变化还好,我们直接积分就可以得到位移和时间的关系了。可是现在F 并不单纯,它里面还藏着x 或t 没有露出来,要想直接积分就比较麻烦。
胡克定律
下一步,我们自然要再去找找F 与x 之间有什么关系。想必你已经知道了,就是牛顿的死对头胡克发现的 胡克定律 。胡克定律表达为如下形式:
F=-kx \\
胡克定律中有两点需要注意, 一是它表达了振子离开平衡位置的位移与所受弹力成正比,二是弹力方向始终与位移的方向相反 (前提是我们把振子的平衡位置定义为原点,即位移为0的位置)。
牛顿与胡克的「联姻」——常微分方程
接下来,让人尴尬的一步就出现了。如果我们把胡克定律中表达的F 带进牛顿第二定律中去,再把常数放在一起,就得到了下面这货:
\begin{align} \frac{\mathrm{d} ^{2}x}{\mathrm{d}{t^2}}=-\frac{k}{m}x \end{align} \\
在数学中为了更一般的讨论,常常把它写成下面这种形式:
\begin{align} m \frac{\mathrm{d} ^{2}x}{\mathrm{d}{t^2}}+kx=0 \end{align} \\
在数学中,这被称为 二阶常微分方程 。叫「微分方程」是因为方程中有自变量的微商;叫二阶是因为微商的阶数最高是二阶的;叫「常」是因为自变量只有一个(即时间" t ,在数学中,还会出现多变量的情况,这个是后话)。
为什么说尴尬呢?你瞧瞧,有着恩恩怨怨的牛顿和胡克虽然吵了一辈子,但是他们在科学上的成就却彼此左手拉右手,至少在描述简谐振动这件事儿上,别提它们有多甜蜜。
那么该如何求解这个二阶常微分方程,来得到位移 关于时间的表达式呢?解法其实有很多,真真是八仙过海,各显神通了。在这里,我介绍两种求解方式,一个用的是费曼的推理手法,另一个复数和指数求解的思路。我们一个个地看。
方式三 费曼的推理
费曼是一位擅长 通过简单的例子去说明高深问题 的大师。比如,1986年,挑战者号失事后,费曼只用一杯冰水和一只橡皮环,就在国会向公众揭示了挑战者失事的根本原因——低温下橡胶失去弹性。而在弹簧振子的问题上,费曼体现了他的另一个能力—— 面对一个一般问题,先从简单的情况入手,抓住事物规律的核心,再去考虑其他情况 。

接下来,就让我们一起,看看费曼是如何推导出振子位移随时间变化的振动方程的。
1. 考虑特殊情况,化简微分方程
上面的二阶常微分方程中有两个常数m 和k ,为分析的方便,我们不妨把m 和k 放到一块儿,并令k/m=1 ,即假设有这样一个弹簧振子,它的劲度系数的数值和物块质量的比值等于1,这个假设显然是允许的。这样,没有常数干扰的微分方程就写成了
\begin{align} \frac{\mathrm{d} ^{2}x}{\mathrm{d}{t^2}}=-x \end{align} \\
至于k/m 不等于1的情况,我们先放一边儿,过一会儿再考虑它。
2. 抓住微分方程的关键性质尝试构造函数
不知你发现了没有,方程(3)其实表达了这么一个意思: 关于时间的函数 x ,在经过两次求导 (即 \frac{\mathrm{d} ^{2}x}{\mathrm{d}{t^2}} ) 后居然变回了自己,还是 x 。只不过多了一个负号 。
到底是什么样的函数具有这样的性质呢?此处迅速在头脑里回忆一下初等函数,我们发现,正弦函数或余弦函数都行。不妨设x=\cos(t)\\
3. 根据物理意义优化函数的表达
我们知道,时间的单位是"秒",而余弦cos的括号里装着的,应该是以"度"为单位的角度量。因此 括号里面不单单是时间 t ,还应该乘上一个量,它与时间的乘积应该是一个角度 。我知道你一定想到了圆周运动的角速度\omega ,因为它乘以时间就是角度。
不过,这里需要提醒一下,我们需要的这个量虽然与角速度在单位上相同,但是它并不是物体旋转时的角速度,因为这里的振子并没有体现出旋转的意思。但是我们依然可以把这个量写成符号\omega_0 。这样,振动方程进一步被优化成了下面这个样子:
\begin{align} x(t)=\cos\omega_0t \end{align} \\
这个函数离我们的目标以经很近了,可是 那个 \omega_0 到底是个啥?它有什么物理意义呢 ?我们还需要进一步探索。
4.把函数尝试代入微分方程
为了理解\omega_0 的物理意义,我们把猜测的x=\cos(\omega_0t) 带入二阶常微分方程中,去看看\omega_0 将会有什么表现。代入后的结果如下:
\begin{align} \frac{\mathrm{d} ^{2}x}{\mathrm{d}{t^2}}=-\omega_0^{2}x \end{align} \\
通过比较(1)、(5)这两个式子我们发现,只要令\omega_0^{2}=\frac{k}{m} ,即这两个式子就相同了。那么\omega_0=\sqrt{k/m} 。
可以看出, 这个 \omega_0 的确跟弹簧的固有属性有关系,那么这个关系体现在什么方面呢?
结合物理情景分析意义
对函数x=\cos\omega_0t ,我们结合实际振动来分析看看。
- 首先振子的位移一定在一个区间内变化,最大值有正负之分,有对称性,而且最小值为0,余弦函数的取值范围是(-1,1),也具有对称性;
- 当时间t=0 时,x 取最大值,这表示振子是从最大位移处开始运动的;
- 振子振动具有周期性,而\cos\omega_0 t 正好是周期函数。
函数的性质与振子的物理性质符合得很好,所以我们有理由相信, 弹簧振子的运动学方程一定具有余弦函数的内核 。
但是还有个问题, 振子的振动周期,到底等于多少呢 ?
这个问题其实很好回答。我们知道,所谓周期,其实就是物体经过一个时间段T 之后,正好回到出发点。而在余弦函数\cos\theta 中,周期是2\pi 。也就是说,当振子运动了t=T 的时间后,\cos(\omega_0 t) 括号中所谓的"角度"\omega_0t ,就将等于2\pi 。这样我们就有\omega_0 T=2\pi ,这样就求得了周期的表达式为:
\begin{align} T=2\pi\sqrt{\frac{m}{k}} \end{align} \\
这个表达式说明什么意思呢?
- 表明了当振子质量越大,振动的周期越大,即振子振动得越慢;
- 表明了当弹簧劲度系数越大,振子得周期越小,即振子振动得越快。这和我们上面得讨论和实验规律相吻合。
说到这里, 对于振子的运动方程,我们不仅把它的盖头掀开了一大半,还顺带求出了弹簧振子的振动周期,还进一步发现了是一个跟周期有关的量,表达了振动的固有属性 。
由特殊到一般,得到通解
通过刚才的分析我们知道,\cos(\omega_0t) 仅仅表达了振子从最大位移处开始运动的情况,此时振子的速度为0,然而, 振子的运动初速度可以不为0啊 。比如本来振子静止在平衡位置,现在让一颗子弹射入振子内部,并从此刻开始计时,那么振子的运动方程就不再是余弦,而要用正弦。
更进一步想想下这个场景,你正在用秒表去记录振子的运动,让秒表指零时为计时起点,此时振子在最大位移处,振动方程正好是余弦。然后牛顿也带着秒表走进来,他刚令秒表从零开始计时(假设你的秒表已经走过了\Delta t 的时间),就发现振子在最大位移的一半处。这个时候,对牛顿而言,他在零时刻看到的振子的位置,应该跟你经过了\Delta t 时刻看到的位置是一样的。因此,牛顿的振动方程应该写作:
\cos\omega(t+t_0) \\
由于t_0 是一个任意的数,此时令\varphi =\omega t_0 ,它也是一个任意的数,这样,方程可以进一步改成x=\cos(\omega t+\varphi) 。
还有最后一个事儿没处理干净,就是振子的振幅,在上面的表达式中,余弦函数的最大值是1,可是我们可以让振子以任意的振幅运动,所以,我们还得把振幅A 添加到方程里面去。最终,振子的运动学方程就变成了:
\begin{align} x=A\cos(\omega t+\varphi) \end{align}\\
这就是以弹簧振子为代表的简谐振动的通解。
方式四 用复变函数的思路
这个思路要感谢知乎大佬 @烤羚羊,他也是从二阶常微分方程入手,在他给出的求解过程一开始和费曼是一样的,都是先 猜想 解的形式。只不过,费曼猜想的是余弦函数,而@烤羚羊猜想的是e 指数,即e^{\lambda t} ,它和余弦函数一样,也可以在经历两次求导后得到于原函数类似的形式。经过一通推导后,得到了简谐振动方程的复数形式如下:
x(t)=r\left[\mathrm{e}^{i(\omega t+\phi)}+\mathrm{e}^{-i(\omega t+\phi)}\right] \\
有兴趣的同学可以跳转到知乎@ 烤羚羊的文章 去看看。
在下一篇文章中,我将从简谐振动的复数形式出发,去看看怎么在GeoGebra中把简谐振动与圆周运动直观地联系起来。
方式五 能量守恒大法好
上面的做法总结起来无外乎两种, 一种是从振子的实验数据出发,去猜余弦函数 (高中教材的做法), 一种是从振子的动力学方程出发,去猜常微分方程的解的可能形式 (费曼的做法和知乎@烤羚羊的做法)。都是 靠猜 。
那有没有什么办法可以不用靠猜,直接通过严谨的数学推导就能得出振动方程呢?有的,就是利用 机械能守恒定律 。这和上面的思路完全不同,【新概念物理学教程·力学】中用的就是这种办法。我们一起看看吧^_^
弹簧振子具有的能量
为了讨论振子的运动学方程,我们先看看 振子运动过程中的不变量 —— 总能量 。
对于宏观的弹簧振子而言,总能量无外乎两种,一种是 振子的动能 ,我们在中学就已经知道它的计算式为\frac{1}{2}mv^2 ,显然它和振子的速度有关系,而速度是位置的一阶导数。另一种是 系统的弹性势能 U(x) ,那么弹性势能的具体表达式又是什么呢?我么一起把它搞出来。
弹性势能的泰勒级数
我以前被泰勒级数这四个字吓住过,不知道是个什么玩意儿,随着认识的加深,我逐渐明白了它的意义——用来近似的。部分读者可能还蒙在鼓里。接下来请允许我对它多唠叨几句。
首先,我们给出弹性势能的泰勒级数展示式。为了讨论的方便,我们把平衡位置记为0点,那么偏离平衡位置的位移和振子的位置在数值上相等,这样,振子的泰勒级数可以表达为如下形式:
U(x)=U(0)+U^{\prime}(0)x+\frac{U^{\prime \prime}(0)}{2 !}x^{2}+\frac{U^{\prime \prime \prime}\left(0\right)}{3 !}(x^{3}+\ldots
大家不要被这么一长串公式给吓着,怎么理解它的意义呢?我们通过分析一副石膏像的素描过程来理解它。

在上图的素描画中,第一步先画出人物的轮廓,虽然它和真实的照片差距很远,但仍然可以知道这画了一个人,我把它称为对真实照片的模拟加入了 一阶近似 ;
接着第二步,对人像的五官进行深入勾勒,这时我们发现摩西的感觉已经出来了,但还是和真实照片有差距,我把它称为对真实照片的模拟加入了 二阶近似 ;
然后到了第三步,画家开始对照片中的光影明暗进行深入分析和表现,使得素描画更加立体丰满,此时的画作和真实照片的差距已经很小了。我把这称为对真实照片的模拟加入了 三阶近似 ;
现在你应该明白了, 只要我们不断地近似下去,让近似项越来越多,我们对原始对象地表现将会越来越逼真 。
回到泰勒级数上去,它干的活儿和上面的素描过程其实是一样的。U(0) 就相当于那一张白纸,U^{\prime}(0)x 就是对弹性势能加了一阶近似,\frac{U^{\prime \prime}(0)}{2 !}x^{2} 就是对弹性势能加了二阶近似,依此类推。
这么做有什么好处呢?它可以帮助我们得到弹性势能的表达式。接下来我们分析一下这些近似的含义和他们的表达式。
1.首先看U(0) ,它表示振子在平衡位置时的弹性势能。根据对称性的方便,我们令平衡位置时的弹性势能为0,即
U(0)=0 \\
2.再看一级近似U^{\prime}(0)x 。这里有个一阶导数U^{\prime}(0) ,它表示什么意思呢?嘿嘿,在中学我们就学过, 弹簧弹力做的功等于弹性势能变化量的负值 ,写成微分形式就是 F\mathrm{d}x=-\mathrm{d}U 。然后把它变革形,就得到了弹性势能一阶导数的表达式:
U^{\prime}(x)=\frac{\mathrm{d}U}{\mathrm{d}x}=F \\
再根据胡克定律,弹簧弹力大小F=kx ,所以最终我们得到了弹性势能一阶导数为
U^{\prime}(x)=kx \\
而当x=0 时,振子处于平衡位置时的弹力为零,把x=0 带入上式就得到弹性势能的一阶导数为0。
3.再看弹性势能的二阶导数。有了一阶导数的表达式,二阶导数自然就可以轻松得到,即
U^{\prime\prime}(x)=k \\
4.最后看高阶项。由于二阶导数已经为一个常数k 了,那么三阶以上的各项就都等于0了。
终于,弹性势能的表达式就被我们搞出来了,即
U(x)=\frac{k}{2}x^{2} \\
换元积分求解
有了动能和势能的表达式,我们就可以得到总的机械能表达式
\begin{align} E=\frac{1}{2}mv^2+\frac{1}{2}kx^2 \end{align}\\
为了等会儿的积分,我们也可以把它改成
\begin{align} v=\sqrt{\frac{2E}{m}(1-\frac{k}{2E}x^2)} \end{align}\\
因为振子振动过程中总能量守恒,所以E 是一个定值常数。为了求解x 随时间变化的函数,我们写出速度的导数形式v=\mathrm{d}x/\mathrm{d}t ,那么有
\begin{align} \frac{\mathrm{d}x}{\sqrt{1-\frac{kx^2}{2E}}}=\sqrt{\frac{2E}{m}}\mathrm{d}t \end{align}\\
接下来就是积分技巧了,我们通过换元法,令\sqrt{k/2E}x=\sin\varphi ,这样分母
\sqrt{1-\frac{kx^2}{2E}}=\sqrt{1-\sin^2 \varphi}=\cos\varphi \\
而且有
\mathrm{d}x=\sqrt{2E/k}\cos\varphi\mathrm{d}\varphi \\
经过这么一折腾,上面第3个式子就被改成了
\begin{align} \mathrm{d}\varphi=\sqrt{\frac{k}{m}}\mathrm{d}t \end{align}\\
然后两边积分,得到
\begin{align} \varphi=\sqrt{\frac{k}{m}}t+\varphi_0 \end{align}\\
再换元到x ,有
\begin{align} x=\sqrt{2E/k}·\sin(\sqrt{\frac{k}{m}}t+\varphi_0) \end{align}\\
终于大功告成,这个表达式和我们的常见表达式 x(t)=A \sin (\omega t+\varphi’) 在意思上是一样的。其中的\sqrt{2E/k} 就是振幅A , \sqrt{\frac{k}{m}} 就是我们之前定义那个\omega 。
最后的话
洋洋洒洒六千多字,不算多但也不算少,经过这么一通分析,我感受到了以下几点:
- 要想认真学懂一个知识,少不了旁征博引,博览群书,不要囿于一家之言 。因为一本书有一本书的观点,它往往会受作者的意图、篇幅、定位等方面的考虑,不一定面面俱到。
- 把学到的知识写下来,讲给大家听,会加深、巩固和检验你对知识了解,结交优秀的人 。其实我是一个很自卑的人,很少跟人交流,加上以前视野不开阔,学习不够深入,对很多知识的认识只是浮于表面。在长尾君的引导下,我逐渐学着去学习,学者写点东西,把学着把学到的东西讲出来。这么做不仅利己,还能利人,还能借此机会认识更多优秀的人,何乐而不为呢?
关于简谐振动的方程,也许还有其它的推导方式,如果你知道的话,欢迎在评论区留言与我分享,让更多的人知道。











