很有意思的问题。
套利策略首先一定是自融资的。定义或有凭证 C_{T} 是一个 \mathcal{F}_T-measurable 的随机变量,即
C_T = C_0 + \int_{0}^{T} H_t d S_t
其中 H_t 就是我们的交易策略,在连续时间下表现为在 \left[ t, \ t+dt \right] 时对股票 S 的持仓比例。那么自融资就时这样一回事:
\sum_{j=0}^{d}{H_t^j S_t^j} = \sum_{j=0}^{d}{H_{t+1}^j S_t^j}
这样一个交易策略会不停地做rebalance,也就是动态对冲。构建这样一个组合的初始净值应该是V_0 =\sum_{j=0}^{d}{H_{1}^j S_0^j}=0 .
对于无风险套利的资产净值 V_t ,有这么几个特征:
- V_0=0
- V_T>0
- P \left[ V_T<0 \right]=0
这个特征十分明显,那就是无风险套利有天然的收敛时间 T 。
而对于统计套利,以及期现套利/跨期套利等等有风险套利,并不存在这样特定的收敛时间,本质上都是asympototic无风险套利,也就是 T\rightarrow + \infty 的条件下,套利都成为了无风险套利。大神Robert Jarrow等人曾针对统计套利给出这样的定义:
- V_0=0
- \lim_{t \rightarrow +\infty} \mathbb{E} \left[ V_t \right]>0
- \lim_{t \rightarrow +\infty} P \left[ V_t<0 \right]=0
- \lim_{t \rightarrow +\infty} \frac{ \mathbb{Var} (V_t)}{t} =0 \ \ \text{if} \ \ P \left[ V_t<0 \right]>0, \ \forall \ t < +\infty
后来他们把第4条做了改进:
\lim_{t \rightarrow + \infty}\mathbb{Var} \left[ \Delta V_t \mid \Delta V_{t} <0 \right] =0
改进的原因在于避免将正的 \Delta V_{t} 也当作风险。
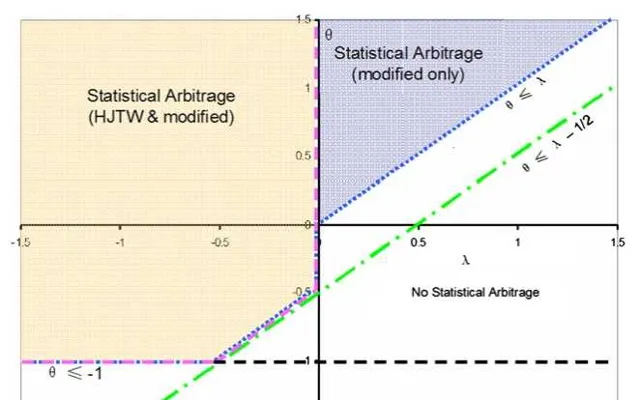
如果假设 \Delta V_{t} 存在一个数据生成过程,即
\Delta V_t = \mu t^{\theta} + \sigma t^{\lambda}z_t
那么对于参数 \theta 和 \lambda 来讲,只有在一定范围内存在套利正收益的可能。反之,就不能称之为套利策略了。