零点是指使z变换X(z)的值为零的z值,极点是指使X(z)的值为∞的z值。如果X(z)是有理分式,表示为:
X(z)=\frac{B(z)}{A(z)}=\frac{b_0+b_1 z^{-1}+\cdots+b_M z^{-M}}{a_0+a_1 z^{-1}+\cdots+a_N z^{-N}}=\frac{\sum_{k=0}^M b_k z^{-k}}{\sum_{k=0}^N a_k z^{-k}}
也可以理解为:
物理意义为,
零极点的影响:
从时间域上,极点和零点会影响二端口网络的瞬时响应(就是大家做仿真时候看的transient)。例如如果有些零极点对会造成电路 输出上升下降时间很慢 。二端口网络拉普拉斯域输出Vout(s)即输入Vin(s)与传输函数H(s)的乘积:
V_{\text {out }}(s)=H(s) V_{\text {in }}(s)=\sum_{j=1}^m \frac{K_H}{s-p_{j H}}+\sum_{j=1}^n \frac{K_{I N}}{s-p_{j N}}
重点关注,零极点对模拟系统的影响。
系统的零极点决定了系统的 频率特性 和 稳定性 。 系统的稳定性与闭环传递函数的极点有关。如果 闭环传递函数的所有极点都在s平面的左半平面 ,即实部都为负数,那么系统是稳定的。如果有任何一个极点在s平面的右半平面,即实部为正数,那么系统是不稳定的。如果有极点在虚轴上,即实部为0,那么系统是临界稳定的,会发生持续振荡。
只 含有左半平面极点的系统才是稳定的 ,因为这样可以保证系统对任何有界输入都能产生有界输出。如果有右半平面极点,那么系统对某些输入会产生无界输出,即发散。如果有虚轴上的极点,那么系统对某些输入会产生持续振荡,即不收敛。
拉氏变换s与实际频率f理解
所谓的零极点,主要是因为在对信号进行频率分析的时候,需要求解系统的传递函数。然而直接求解过程中,由于微分方程、积分方程等的复杂性,对于系统的分析具有较高的难度。通常的处理方法是对系统的微分方程进行傅里叶变化或拉氏变换(重点理解拉氏变换),拉氏变换将传递函数从时域转换为频率,将实际物理中的频率f转换为s域中的s。即:拉氏变换可以将时域的微分方程转化为复频域的代数方程,从而简化了求解过程。 实际信号的频率和拉氏变换s中的角频率是有一定关系的 。实际信号的频率是指信号或系统在时域上周期性变化的快慢,单位是赫兹(Hz)。 拉氏变换s中的角频率是指信号或系统在复频域上旋转的快慢 ,单位是弧度/秒(rad/s)。两者之间的转换关系是: ω=2πf 也就是说,当实际信号的频率增加时,对应的角频率也会增加,反之亦然。但是, 实际信号的频率只能取正值 ,而 角频率可以取正负值 。就是公式的值可以转换,但是f只能有正值,而角频率ω却能有负值,数学符号上的含义是ω取负时,复平面代表s值按照逆时针旋转。 当ω绝对值相同,大小相反,代表着物理中相同的频率点 。
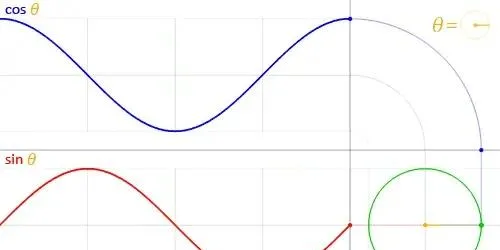
这是因为 拉氏变换s中还有一个衰减因子σ ,它决定了信号或系统在复频域上的衰减或增长。当σ为正时,信号或系统是不稳定的,当σ为负时,信号或系统是稳定的。
拉氏变换中的ω和相位θ的关系
拉普拉斯变换中s表达式中的ω和复平面旋转的θ的关系是这样的:
左半平面极点稳定理解
理解了拉氏变换s和实际频率的关系后,所谓的左半平面极点, 指的是该系统的传递函数中,s的解为负数或者实部为负数的共轭复极点,该系统就可能稳定 。 左半平面极点是指在复平面上,实部为负的极点 。它们通常与系统的稳定性和因果性有关。根据拉普拉斯变换和z变换的关系,s平面的左半平面映射到z平面的单位圆内部,所以 线性时不变因果稳定的系统,其极点都在s平面的左半平面 。
左半平面和右半平面极点的区别是, 左半平面极点的实部为负数,右半平面极点的实部为正数。(都是指的拉氏变换中s的解,该解为负数,即为复平面) 他们的物理含义是:
只有左半平面极点的系统才能稳定, 是因为 这样可以保证系统对任何有界输入都能产生有界输出 。如果有右半平面极点,那么 系统对某些输入会产生无界输出,即发散 。 如果有虚轴上的极点,那么系统对某些输入会产生持续振荡,即不收敛。
理解右半平面极点造成的不稳定
右半平面极点会使系统的相位提前,并且在高频时增益不会衰减到零,而是趋近于一个常数值。这样就会破坏系统的相位裕度和增益裕度,使系统无法满足奈奎斯特稳定判据,从而引起系统的不稳定性和振荡。
共轭复极点理解
当在解拉氏变换后的传递函数时,有可能会得到s等于共轭复数的结果,或者称之为共轭对。 即,s的解实部相同,虚部互为相反数。例如: s_1=σ+\text iω和s_2=σ-\text iω 当σ为负数时,该系统稳定;当σ为正数时,该系统发散。 共轭复极点的物理含义和后果取决于具体的应用场景,但一般来说,它们与系统的 稳定性、频率响应、带宽、相位等 有关。 例如,在电路分析中, 共轭复极点可以用来实现带通滤波器 ,提高系统的选择性和灵敏度。 共轭复极点的实部决定了系统的阻尼系数 ,如果实部为负,系统是稳定的;如果 实部为零 ,系统是临界稳定的;如果实部为正,系统是不稳定的。
共轭复极点 会造成系统的振荡现象 ,振荡的频率由极点的虚部决定,振荡的幅度由极点的实部决定。稳定系统的共轭复极点还会造成电路的过冲,如下图所示:

共轭复极点造成过冲现象 如何避免共轭复极点的出现,主要取决于系统的开环传递函数的特性。一般来说,有以下几种方法可以尝试:
单极点系统
单极点系统是一种只有一个极点的线性系统,其传递函数可以表示为
H(s)=\frac{A_0\omega_0}{s+\omega_0}
其中, A_0 是直流增益, \omega_0 是极点频率。
https:// zhuanlan.zhihu.com/p/20 918998一个典型的单极点系统电路如下图所示:
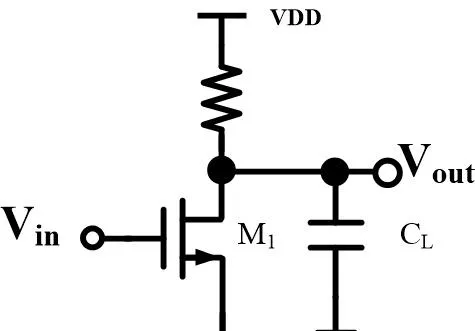
一个nmos和一个resistor,组成了一个基本的common-source amplifier。 暂时忽略Cgs、Cgd等寄生电容造成的高频零极点。这个电路便是一个单极点系统:唯一的极点就在输出Vout那里。(负载电容 C_L 和输出端等效电阻形成RC并联谐振无穷大) 该电路的传递函数为: H(s)=\frac{A_0}{1+\frac{s}{\omega_0}} 据此画出该单极点电路的波特图:
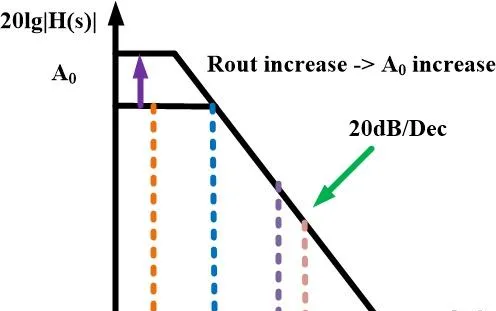
单极点系统有以下特性:
要分析单极点系统,可以使用波特图(Bode plot)来表示系统的幅频特性和相频特性。波特图可以用以下步骤绘制:
单极点系统的频率响应表达式可以用以下公式表示:
高阶无源网络极点的判别(时间常数法)
概述
高阶无源网络极点的判别所使用的时间常数法是基于以下原理:
基本原理
要对一个系统进行零极点分析,首先要知道单极点系统和两极点系统的基本分析,然后化繁为简,采用单极点近似得到系统的大致频率响应特性。 电路极点表达式经过化简后,可以看到一次项系数为时间常数求和,二次项系数为时间常数求积,因此只要得出时间常数,即可直接写出电路的极点表达式。
未完待续









