前集回顾
话说上期,我们聊到了,如何在现实世界中,通俗地理解「傅里叶变换」、「拉普拉斯变换」和「Z变换」的奥妙。为加深印象,咱在开启本篇的话题之前,再做个前集回顾:
在上篇文章【干货周记:三分钟弄懂零极点图(上)(番外篇2)】中:我们搞懂了,「傅里叶变换」和「欧拉公式」这对组合,能完美地把时域信号,映射到了频域,从而让咱能多了个视角去观察世界。
但大千世界,无奇不有,有些信号吧,它不可积,也不稳定,如果要分析它们,那「傅里叶」的法力就不够用了,咱得用带「衰减因子」的「拉普拉斯变换」稳住局面。

同时,咱也清楚了:为啥「傅里叶变换」只是「拉氏变换」的一个切片,为啥「Z变换」只是叠了层「甲」的「拉普拉斯变换」。有了这些基础,咱在上期的结尾部分,终于引出了S域和Z域的零极点图。
下面,咱尽量简化,不讲太细,直接把干货浓缩成「作业指导书」,捧起来就知道该怎么用。话不多说,上干货。
啥是零极点图?
看到下面两幅零极点图,你可能会想:这玩意儿也太抽象了吧,它真能帮咱分析系统特性吗?别急,咱一步步来。
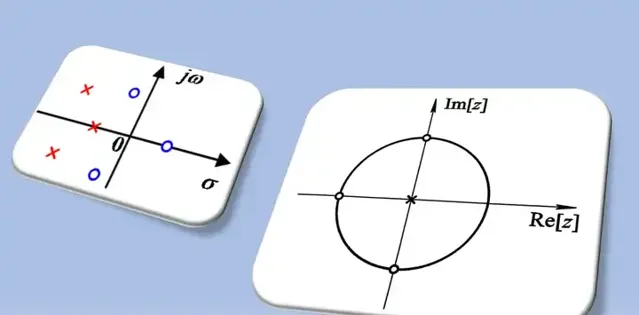
那啥是零极点图呢?它本质上就是 「拉氏变换」和「Z变换」等的系统特性表示图。 基于它,你可以透过现象看本质,一眼洞穿其系统特性。听着挺玄乎,其实也没啥神秘的,看完这篇文章,你就明白咋回事了。
咱先回忆下,「 傅里叶变换」的系统特性表示图是什么? 是 波特图 (即幅频图和相频图),当看到下左图时,你很快就能认出,这是个低通滤波器系统,因为其对高频部分有衰减,甚至哪里可能有个极点,你都能一目了然。
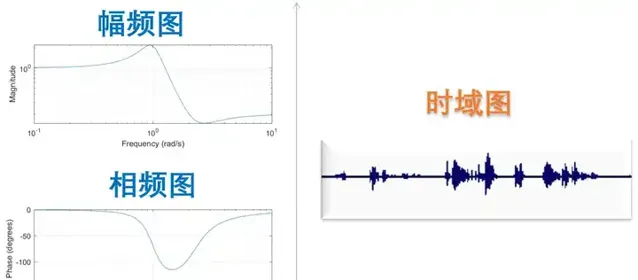
如果说「傅里叶变换」的系统特性表示图,是2D的波特图,那多加了一维的「拉氏变换」和「Z变换」的系统表示图,理应用3D图来表示。但以S域零极点图( 下右图 )为例,其本质也就是 下左图 的俯视图,幅度的凸凹(即极点和零点),分别用 x 和 o 表示。看上去还是2D的,不够炫酷。

这主要是因为,早期的前辈们,受限于当年的计算机性能,无法随心所欲地做仿真/建模,更不好在纸上呈现3D,不得已才祭出了「零极点图」这种近似分析工具。
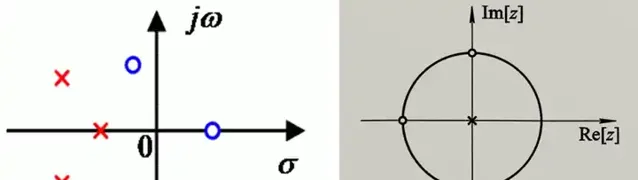
说到这,「零极点图」似乎还有点复古风,我更喜欢称之为2.5D图。
类似的表现手法,在STFT或小波变换上也有所体现,区别只是去掉了「衰减因子」维度,引入了「衰减因子」维度,把用「零极点」表示幅度变化趋势,改成了用「色彩强弱」表示幅度。

看清「零极点图」真面目
说到「零极点图」,我们要先搞清楚是哪个域的图。「S域」(拉普拉斯域),还是「Z域」?一般而言,模拟系统分析和滤波器设计,常在S域做分析;而数字系统与滤波器设计,则常在Z域做分析。
另外,零极点图中,无论S域还是Z域,X都代表极点,也是幅度凸点。O都代表零点,也是幅度凹点。这种表达方式,和高中物理中的磁感线方向的呈现手法,有些类似。
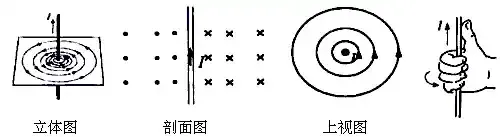
S域「零极点图」分析的核心:
一、横轴代表衰减程度(左侧有衰减,更安全),纵轴代表频率,一般仅关注上半轴/正频率,原点为f=0处,Y轴向上是f=+∞方向,可基于此看频响特性。
二、极点会造成幅度凸点(Peak),零点会造成幅度凹点(Notch)。无论零点还是极点,离横轴原点越近,其影响力就越大。
三、图上的每一个点(σ+jω),都代表了该系统在对应频点上的分布,以及其对应的衰减特征。
四、当极点落在σ=0的虚轴上时,系统临界稳定。极点落在左半平面时,系统稳定,极点飘到右半平面时,系统不稳定,会自激、会啸叫。
举例: 下图中,在w=0处有两个极点凸起,很显然,这是一个二阶LPF低通滤波器,综合滚降斜率为-40dB/Dec
同样的,不难得出以下结论:

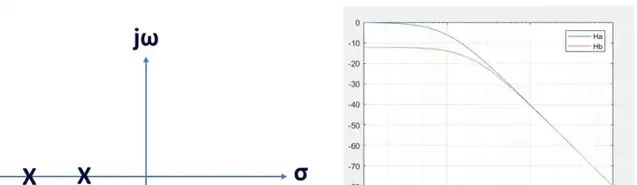
这是个一阶高通滤波器HPF。虽然在ω=0处有极点也有零点,但离原点近的影响力更大,其主导作用,所以在这里ω=0(DC)时,零点赢了,故在右面的幅频图中f=0处幅度也为0,很明显的HPF。
类似的,下面的零极点图,表示的是个带通BPF。正轴极点对应的ω值,也对应了右面频点的凸起位置。

Z域「零极点图」分析的核心:
一、Z域零极点图,是极坐标形式。离单位圆的距离代表衰减程度(单位圆内有衰减,更安全),旋转角度可代表频率(φ=0时为DC,φ=π时,ω=fs/2,即待分析信号的奈奎斯特带宽)。通常分析时,只需看第一第二象限(φ=0~π)

二、极点会造成幅度凸点(Peak),零点会造成幅度凹点(Notch)。无论零点还是极点,离单位圆原点越近,其影响力就越大。
三、图上的每一个点Re(z)+Im(z),都代表了该系统在对应频点上的分布,以及其对应的衰减特征。频点信息可根据角度信息解析得出。
四、当极点落在单位圆上时,系统临界稳定。极点落在单位圆内,系统稳定,极点飘到单位圆外,系统不稳定,会自激、会啸叫。很多时候设计时,需要留有足够的裕量,否则可能会导致极点飘到单位圆外。(如ANC系统的次级路径变化时,可能会导致系统自激振荡)
无论S域还是Z域,一句话小结: 本质上就是在系统中,通过设计零极点个数,及其摆放位置,使得系统达到目标特性。 举例:ANC系统,通过测量和理论计算,可以得到前馈系统的目标传函,工程师们可通过在Z平面上,摆放设计好的零极点,从而达到目标特性。
然而,「零极点图」有优点也有缺点,它并非人见人爱。
优点: 简单、直观,快。通过「零极点图」这个可视化平台,设计者可直观地分析出系统的频响特性,快速分辨系统稳定性,而不需要繁琐的计算。举例:在用「零极点图」设计滤波器时,工程师直接就开启了「上帝视角」,通过调整零极点位置的摆放,就能灵活地改变系统特性。

三个缺点 :
一、线性时不变的枷锁。「零极点图」主要适用于」线性时不变「系统分析,而对」时变系统「无能为力。
二、精度有限。无法提供精确的幅度信息,也不能精确得到幅频和相频响应的具体曲线形状。
三、对超高阶系统,可读性会下降。很难想象,面对一大堆零极点密密麻麻的分布图,脑子里原始洞察力,会何去何从。
总之,零极点图是个高效直观的系统分析工具,但它也有自身的局限性,对复杂系统或需精确信息的场合,结合其他「武器」使用,效果最佳。
最后,咱再留个思考题:上述只是针对幅频做了分析, 那相频呢? 零极点的影响又当如何分析,相位裕度该怎么把握,如何摆放零点,能把不稳定系统,补偿为稳定系统?欢迎私信/留言。
End
Roy个人观点,仅供参考。
干货周记系列 ,我们会持续更新下去,后续会逐步深入,更具体。在「干货周记」中,保持更新的还有:
音频产品/市场/技术(消费+汽车,模拟+数字),
汽车产品/市场/技术(座舱+智驾),
可穿戴健康系列
如果你对数码产品、英语学习和励志成长也感兴趣,也可关注各平台上的同名视频账号:微博、抖音、视频号,B站、小红书:科技朋克Roy,知乎:Roy








