虽然是学控制的,虽然我的id名也跟控制相关,但我不喜欢复杂的公式推导。在遇到纷繁复杂的数学公式时,我也跟题主一样,想搞明白这些数学表达背后的物理意义到底是什么。想明白这些,再去看那些数学公式,会觉得非常合适,非常简明,非常优美,必须这么定义才能表达的这么清晰。
在讲零极点的物理意义之前,我们先讨论下什么是线性定常系统,我们平时遇到的大多数是线性定常系统,或者可以简化为线性定常系统。
线性定常系统(Linear Time-Invariant System,简称LTI系统)是一类特殊的线性系统,它同时满足线性(Linearity)和定常性(Time-Invariance)两个条件。
1. 线性(Linearity):对于任意两个输入信号x1(t)和x2(t),以及任意两个常数a和b,系统的输出满足以下关系:
y(t) = a * x1(t) + b * x2(t)
这意味着,当输入信号进行线性组合时,系统的输出也是对应信号的线性组合。
2. 定常性(Time-Invariance):如果系统的输入信号在时间上平移一个常数t0,那么系统的输出信号也会在时间上平移相同的常数t0。换句话说,系统的响应与输入信号的起始时间无关。用数学表示为:
y(t - t0) = L[x(t - t0)]
其中,L表示系统对输入信号的作用。
线性定常系统的数学模型通常可以用线性常微分方程(Ordinary Differential Equation, ODE)或线性差分方程(Difference Equation)来表示。在频域分析中,线性定常系统的特性可以用传递函数(Transfer Function)来描述,它表示了系统输出与输入之间的频率响应关系。
一个线性定常系统传递函数可以表示为:

线性定常系统具有许多良好的性质,如叠加原理、稳定性、可控性和可观测性等。这些性质使得线性定常系统在理论分析和实际应用中具有很高的价值。许多工程问题,如电机控制、电路分析、信号处理、控制系统设计等,都可以归结为线性定常系统的分析和设计问题。
我们再举个栗子,理解下线性定常系统的两个特性–线性和定常性:
一个和尚念经,用x1(t)表示;我们听到的梵音用y(t) 表示。整个场景定义为:y0(t)=x1(t)。方丈来视察,和尚加大a倍音量念经,则我们听到的梵音音量变大了a倍, 则 y1(t) = a * x1(t) ,体现了"线性"特点;
这时又来了一个和尚也大声念经,则我们另一只耳朵又听到y2(t) = b* x2(t),我听到的梵音总和是y(t)=y1(t)+y2(t),体现了"叠加"特点。
所以听经文是个线性系统。
另外,我早上听,就早一点心灵得到净化,早一点有所顿悟;晚上听,就会有一天的延迟(t - t0),用数学表达一下:y(t - t0) = L[x(t - t0)],L表示我不一定都听懂了,经文在传输过程中有所衰减。体现了"定常"特点。
所以听经文是个线性–定常系统。
根据以上讨论,可以推导出线性定常系统以下特点:
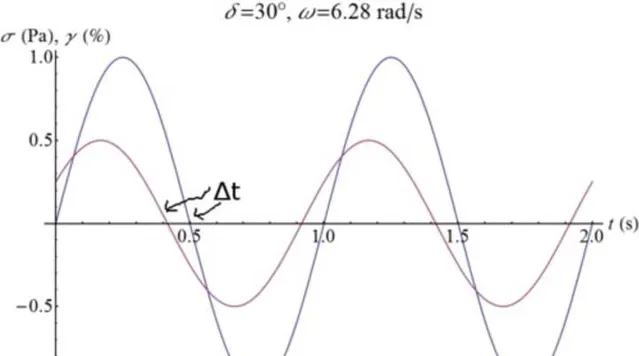
系统输入一个正弦波激励时,输出也是正弦波,频率不变,幅值发生变化,相位有一定延迟。
控制系统中的零极点物理意义在于:
1. **零点**: 零点表示系统在某一特定频率处对输入信号的响应为零。在该特定频率处,输入信号幅值不为零,系统输出为零。零点处的频率通常对应于系统的反谐振点或滤波器的通带截止频率。
接着用上面的栗子,当诵经频率上升到20kHz或者低于20Hz时,你即使站在僧人旁边,也听不到他的声音。所以可以推断,人听觉系统的零点是20Hz和20kHz。
2. **极点**: 系统输入幅度不为零,而系统输出为无穷大(系统稳定破坏,发生振荡),此频率值即为极点。极点表示系统在该特定频率处对输入信号的响应达到最大,通常对应于系统的固有频率或滤波器的阻带截止频率。
继续用上面的栗子,当诵文频率正好处于听觉系统的固有频率时,你即使与僧人远隔千山万水,处于无限远处,也可以听的清清楚楚。这就是失传多年的武功秘籍"千里传音"的理论依据,233。
我们再看看零极点的数学描述:
讲线性定常系统传递函数:

写成零极点形式为:

零点是使H(s)幅值为零的点,当且仅当分子项N(s)为零时,H(s)=0,即:
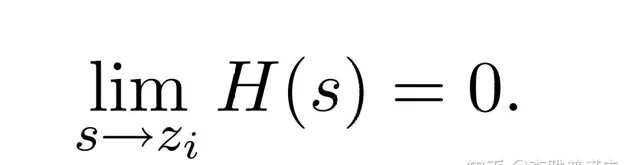
极点是使H(s)幅值为无穷大的点,当且仅当分母项D(s)为零时,H(s)=∞,即:

有没有感觉这些公式看起来舒服多了,简洁、准确,不用像我一样,絮絮叨叨那么多。









