講一個調和分析中很經典的反例吧。1917年日本數學家掛谷宗一(Soichi Kakeya)提出了如下的問題:
設某個日本武士在上廁所時被偷襲,他只能揮動長為1的武士刀應戰。請問在他將刀揮動一周的過程中,掃過的面積最小為多少?好吧,雖然我覺得問題背景不用敘述得這麽具體啦……不過用數學語言描述的話,這其實就是下面的問題:
設平面點集S在每個方向上都含有一條長為1的線段(這樣的集合稱為Kakeya集),請問S的面積(測度)最小為多少?當然按Kakeya的本意,應該要求長為1的線段能夠連續轉動(相應的集合稱為Kakeya needle集),不過這算是個小的技術問題,暫時不用在意。
經過簡單的嘗試,容易猜想在凸集情形,最小面積由高長為1的正三角形實作,其值為1/\sqrt{3} ;這點後來被Pál所證明。對於非凸集,Kakeya本人猜測最小面積應由某個三尖內擺線實作,但一直無人能夠證明或否認這點。
到了1919年,前蘇聯數學家Besicovitch在對其他問題的研究中也遇到了上述集合。結果他證明了令人驚訝的結論:
Kakeya集的測度可以為0。這當然完全解決了Kakeya問題;利用Pál的一個技巧,我們可以從測度為0的Kakeya set構造出測度任意小的Kakeya needle集(註意Kakeya needle集的測度不能為0)。因為Besicovitch的貢獻,現在我們有時也稱Kakeya集為Besicovitch集。
Besicoovitch的構造後來被Perron, Rademacher, Schoenberg,Fisher等人改進過;這裏我們介紹一種稱為「Perron樹」的較為簡單的構造。限於篇幅我們只證稍弱一些的結論,即Kakeya集的測度可以任意小。以下證明取自Markus Furtner的學位論文(見[2])。
固定實數\alpha\in(1/2,1) 和正整數k,以|*|表示面積。對任何三角形T,考慮如下的構造步驟:
作T底邊上的中線,將T分成兩個小三角形L和R。將右邊的小三角形R平移至R',使其底邊與L重疊,且重疊部份長為T底邊長的(1-\alpha) 倍。記T^*=R'\cup L ,由初等幾何可證明T^*=B\cup C\cup D ,其中B是與T相似的三角形,相似比為\alpha ;C和D是兩個三角形,其面積各為(1-\alpha)^2|T| ,如圖所示。為簡便起見我們將稱B為T^{*} 的「核心」,C和D稱為「分支」。
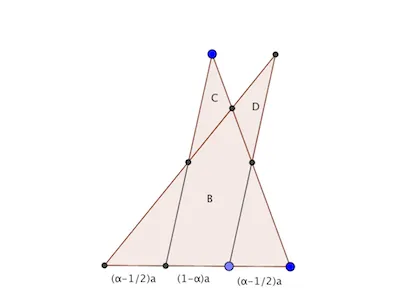
現在取一個高長為1的正三角形T,將T的底邊作2^k 等分,記所得的小三角形從左至右為T_0^0,\cdots,T_0^{2^k-1} 。對每個0\leq j\leq 2^{k-1}-1 ,對三角形T_0^{2j}\cup T_0^{2j+1} 進行操作(實際上操作是對兩個三角形T_0^{2j} 和T_0^{2j+1} 進行的),設所得圖形為S_1^j ,其核心為T_1^{j} 。對0\leq j\leq 2^{k-2}-1 ,容易證明T_1^{2j} 和T_1^{2j+1} (在適當平移後)可以作為某個大三角形對應的L和R,因此對這兩個三角形進行操作,得到圖形S_2^j (註意,此時S_1^j 的分支部份也進行了相應的平移),設其核心為T_2^j 。如此繼續下去,最後得到一個圖形S_k^0 。下面我們證明S_k^0 的面積不超過T的面積的\alpha^{2k}+2(1-\alpha) 倍。
實際上,對0\leq m\leq k ,記A_m=\sum_{j=0}^{2^{k-m}-1}|S_m^j| 。首先A_0=|T| ;對於A_1 ,它將等於所有S_1^j 核心與分支部份面積之和。易知核心部份面積之和為\alpha^2|T| ,而分支部份面積之和不超過2(1-\alpha)^2|T| 。因此A_1\leq (\alpha^2+2(1-\alpha)^2)|T| 。對於A_2 ,它不超過所有S_2^j 核心部份與其對應的分支部份面積之和,再加上所有S_1^j 分支部份面積之和。因此A_2\leq (\alpha^4+2\alpha^2(1-\alpha)^2+2(1-\alpha)^2)|T| 。如此下去,我們得到A_k\leq \bigg\{\alpha^{2k}+\sum_{n=0}^{k-1}2\alpha^{2n}(1-\alpha)^2\bigg\}|T|\leq (\alpha^{2k}+2(1-\alpha))|T| ,即所欲證。
現在我們取\alpha 充分接近1,然後取k充分大,即可使S_k^0 的面積任意小。接下來我們證明,對位於T的頂角及其對頂角內的任一方向,S_k^0 均含有該方向上長為1的線段。這實際上是顯然的;註意S_k^0 等於T_0^j(0\leq j\leq 2^k-1) 這些小三角形的適當平移的並。因為對所說的任一方向,存在該方向上的一條線段完全位於某個T_0^j 中(只需取從頂角頂點出發,沿該方向的線段),因此也存在該方向上的一條線段完全位於S_k^0 中。
最後我們取S_k^0 的三個適當的旋轉的併集,就可以得到面積任意小的Kakeya集。
至此問題就完全解決了。然而當時並沒有人意識到,這個集合對調和分析的命運也有很大的關系。當然那就是另外一個故事了。
參考文獻:
[1]
https:// en.wikipedia.org/wiki/K akeya_set[2]
http://www. mathematik.uni-muenchen.de /~lerdos/Stud/furtner.pdf










