學物理的強答一波。
我目前見過最神的數學知識,或者是一個工具,要數李代數裏的Dynkin diagram了,它可以直接把一個本科高年級的數學問題轉化為一個小學生都會的問題,雖然小學生不會理解它背後的數學意義,但是會了這個工具,還真能把大學生的題做出來。
數學裏直接暴力證明兩個李代數同構,或者證明誰是誰的subalgebra,往往是個比較復雜的工程,尤其是當研究的代數變得復雜的時候。但是所有的semi-simple Lie algebras(準確一點說是它們的complexfication),可以根據它們的roots被歸類成下面這幾種Dynkin diagrams。

記得初學李代數的第一道作業題,老師讓我們證 SU(4) 和 SO(6) 的李代數同構,那時候還嘗試用6維的 \gamma 矩陣去同時構造這兩個代數generator間的對易關系,算了幾頁紙才解決,結果學了Dynkin diagram之後,知道 SU(4) 李代數對應上面 A_{3} 的圖, SO(6) 李代數對應 D_{3} 的圖,它們倆都是三個黃點連起來,長得一樣,所以就同構了,一秒鐘,用眼睛看,就能得到結論。復雜的數學題變成了一個認圖的問題,知道了規則,真的是小學生都會了。
除此之外,引入extended Dynkin diagram的概念,還可以用來證明一個李群是另一個李群的子群。
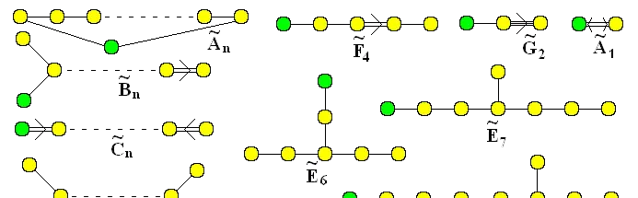
把extended Dynkin diagram拿掉一個點,剩下的圖所對應的李代數就是之前extended的圖對應的李代數的subalgebra。比如從 \widetilde{E}_{8} 裏拿掉最中間那個黃點,剩下兩個一模一樣的四個黃點串聯,每個四個黃點相當於一個 A_{4} ,就能證明 SU(5)\times SU(5)\subset E_{8} 。也是一秒鐘就能做出來的問題,但如果從基本定義暴力算,那花的時間不知道有多少倍。
當然Dynkin diagram是個比較基礎的概念,學過李代數的人都知道,作為數學知識本身沒有鶴立雞群的地方。而且之所以用它證明同構或者子群這麽快,是因為復雜的步驟在構造這些圖的時候已經有人幫你做過了。它讓我「驚呆」的點在於,套用起來是真的方便。我沒見過用其簡化問題前後,問題難度差距如此之大的數學工具。學的時候我就感嘆這簡直絕了。










