給你舉個例子吧。
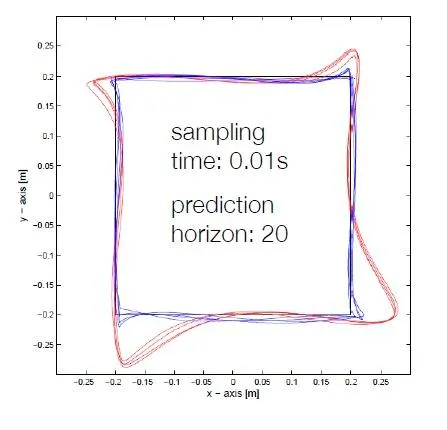
下圖是分別用LQR和MPC兩種演算法來控制一個小球的軌跡讓小球的軌跡盡可能接近黑色框。紅色是LQR控制下小球的軌跡,藍色是MPC控制下小球的軌跡。你可以明顯看到MPC控制下的軌跡和理想軌跡更接近,但LQR在拐角處過沖太大了。
為什麽呢?因為在未到達一個換向點(比如左上角頂點)之前,MPC就已經「看」到了這個點了,MPC提前知道這個點的存在,並在未抵達這個點之前就開始減速了。MPC能做到這點是因為軌跡已經作為約束寫進最佳化問題了。
底下有人說LQR不也是MPC的一種嗎?這個問題問得非常好。LQR只能根據固定的系統模型(狀態空間A,B,C,D矩陣一直不變)向前推演,推演的只是系統模型的發展行為,但是對外界這個硬約束是是一無所知的。設想一下,軌跡沿著最上面那根黑線向左邊走,走到頭突然被告知你要向下轉向了,LQR此時才會開始調整方向,所以過沖是很大的。
在所有要求精確軌跡規劃的場景以及系統有硬約束的場景(大到無人駕駛小到3D印表機打精細圖案)MPC的效能是非常優秀的。
後續我會仔細檢查,如果我有口誤我還會繼續修改。











