不看公式版:
日常的三態變化,就是所謂的一階相變。其特征就是相態轉化過程中呈現出一種不連續性。與此相對應,還有更加復雜的連續相變。一般的熱力學描述(如對稱性破缺)並不能回答題主的問題。因為這些描述中其實首先預設了氣液固三態的存在,然後再用熱力學函數來分析三態變化。但是 題主的問題恰恰是我們的預設前提 ,也就是說:
為什麽會有氣、液、固三種典型狀態?而不是
在已知存在氣液固三態的前提下,如果解釋這三態的區別?首先這裏我用平易近人的方式來說一下。
一階相變的不連續性
其實,氣態是一種最容易理解的狀態。在氣態下,分子距離很遠,並且分子運動劇烈。因此分子間的束縛 - 分子間力相對而言就非常弱,可以忽略掉。當我們把分子間力忽略掉的時候,分子就像是一堆相互碰撞的硬球,這就是理想氣體。
固態也是一個相對容易理解的狀態 - 它是一種有序結構。在這種結構中,每一個分子都找到了與周邊分子相互作用勢能最低的位置。因而形成了最穩固的狀態,這就是晶體。
液態介於其間,相對就復雜得多。簡言之,就是因為分子運動足夠劇烈,導致總是有些分子不安分地呆在勢阱種。分子間的相互束縛總是快速地斷開、連線,導致它們相互滑移。但是這些運動又不夠劇烈到它們從相互作用之間逃離,變成自由分子。
三態變化中容易理解的是,從氣體逐漸降溫,它們會漸次經歷以上三種狀態。但是,不容易解釋的是,當我們對氣體降溫,直至最後結冰,這整個過程中,出現了兩次不連續的跳躍。這兩次跳躍就把狀態分成了三個截然不同的聚集狀態。所以關鍵的問題是:
這種不連續性是如何產生的?在不連續跳躍的時候,為何會有兩種不同的聚集狀態並存?
我們用水來做例子說明這個情況。我們想象有一個系統,是一箱水蒸氣。現在我們開始向外抽取熱量。隨著熱量的向外傳遞,蒸汽的溫度不斷降低,體積不斷縮小。達到沸點的時候,溫度則不再降低,這時候液態水就形成了。此時兩種聚集狀態同時出現,中間有明顯界面。
也就是說,這是一種不連續的變化:水蒸氣並不是一直連續降溫,體積一直連續縮小的。它會在某個溫度(沸點)突然發生了階躍式的變化:體積突然大幅收縮,熱力學性質突然發生跳變。而這種變化就對應著液態水的生成。這種突發的不連續性,就把水的狀態分割成氣液兩態了。
同理,當我們繼續降溫,就會又出現一個不連續的變化。這個不連續性,就把水的狀態分割成液固兩態了。
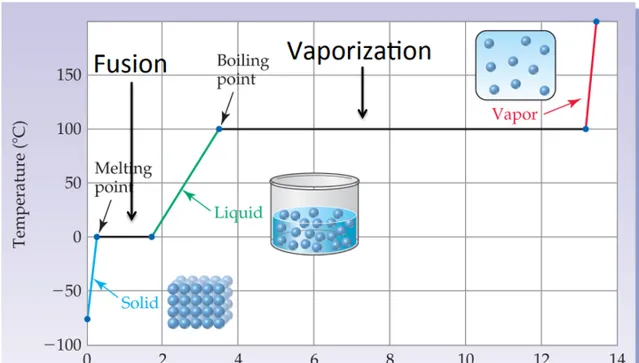
我們不妨來開一下腦洞:我們來假想一下,如果在降溫過程中,蒸汽可以連續地變成水,然後連續地變成冰。也就是說,隨著降溫,蒸汽體積不斷縮小,密度不斷增加,然後漸漸地變成了水(不存在兩相並存的過程)。然後隨著持續降溫,水漸漸地粘稠,變成果凍狀態,然後果凍漸漸變硬,最終變成冰。
在這種假想的情況下,我們會覺得水只有一種相態。他只不過是密度和「硬度」的連續變化而已。
現在,正是因為在過程中出現了兩次不連續過渡,才讓我們產生了「氣液固是截然分立的相態」這種概念。
相的穩定性
那麽,為何會有這種不連續變化呢?這是 熱力學失穩結果 。也就是說,當蒸汽降溫、收縮的過程中,會在特定的時候進入到一種 不穩定的過渡狀態 中,這種過渡狀態無法穩定存在,會自發崩解為兩個穩定的相態。
我們這裏先說一下關於熱力學穩定性的結論:
一個熱力學狀態的穩定性條件是,它的比熱必須大於零,或者說它的膨脹率必須大於零。
這裏稍加說明。為何有這種條件。有興趣的話,可以看後面嚴格的熱力學推導。
比如說, 如果一個系統的比熱小於零。那麽會發生什麽呢?
如果系統比熱小於零,意味著當它向外散失熱量時,它的溫度上升,反之如果它吸收熱量,則溫度下降。我們想象一個孤立系統,它無時無刻面臨著內部的漲落 - 當然,這些漲落的波動非常小。在一個小局部,突然產生了一個小的波動,使得它的產生了一點向外的凈能量流動。那麽:
- 由於負比熱的存在,導致它的溫度上升。而同時,它的周邊會接收到傳入的熱量,因而同樣道理導致周邊的溫度下降。
- 這樣一來,就會形成一個溫差。
- 這種溫差會加速這個局部向外的熱量流動。
- 因此,這會進一步導致該局部的溫升和周邊的溫降,進而加大溫差。
- 從而加劇熱量傳遞……。
這就形成了一個 正反饋 。導致系統平衡的崩潰。這個局部的溫度迅速上升,而周邊則溫度迅速下降。
同理, 如果一個系統的膨脹率小於零,那麽會發生什麽呢?
一個負的膨脹率意味著,當系統的壓力增加的時候,它的體積將會膨脹;壓力減小的時候,體積縮小。那麽,當系統中產生一個小波動,那麽:
- 局部壓力增加,體積膨脹。
- 體積膨脹導致其壓縮周邊的體積,周邊體積縮小,因此壓力縮小。
- 這樣一來,該局部壓力增加,周邊壓力降低,就形成了壓力不平衡。
- 這種壓力不平衡導致這個局部繼續膨脹,壓力繼續增加。
- 因而周邊體積繼續縮小,壓力繼續降低。
- 因此,壓力不平衡加劇。
- ……
這就形成了一個 正反饋 。導致系統平衡的崩潰。這個局部的壓力迅速上升,而周邊則壓力迅速下降。
氣液相變
那麽,這種穩定性條件又和相態變化有何關系呢?
答案是, 從氣態到液態的變化過程中,中間的過渡狀態是不穩定的。因此氣體會直接跳過這種過渡狀態變成液體。
從氣體向液體過渡的過程中,理論上的確存在一個連續的過渡狀態。但是,這種過渡狀態有負熱容或負膨脹率。
這個負熱容是怎麽來的呢?我們可以從分子間力說起。 分子間力是一種短程力 ,它隨著距離迅速衰減,只有當分子十分靠近的時候,才會發生作用。
氣體狀態下分子間力可以忽略,但是當分子間距離足夠接近、且運動比較溫和的時候(溫度較低時),它們之間的吸重力就不可忽略了。而負熱容和負膨脹率的性質就是由分子間力引起的。
我們先來看看這裏的負膨脹率是如何起作用的。具體講,在此時,如果系統的局部發生一個波動,導致該處分子間隙變小,會發生什麽呢?很顯然,
而同時,該局部的周邊會發生反向的正反饋:
這就是 負膨脹率 的影響。
我們也可以換一個角度,從 負熱容 的角度來說這件事。當系統向外放熱的時候,體積縮小。由於分子重力的作用,導致它的勢能下降。勢能的下降就會使得分子動能上升。因此它的溫度反而上升。溫度上升導致它放熱更快,這也是一個正反饋。我們前面看到,這是一種不穩定的狀態。因此,這種過渡狀態無法存在,它會迅速崩解為穩定的液態和氣態,成為兩相並存的狀態。這就是 負熱容 的影響。
也就是說,當分子間吸重力開始起作用的時候,理想氣體的那種自由分子的狀態就被打破了,它變得不穩定,要麽倒向氣態,要麽倒向液態,而不可能穩定地存在於氣液的過渡態。因此,只有兩相並存的狀態,而沒有兩相過渡的狀態(特殊情況下會存在,但是極不穩定)。
這個過程和 黑洞的形成 原理其實是類似的。在自重力系統中,一個系統的熵最大狀態不是均勻分布的狀態。這就是為何星雲會聚集變成恒星。分子間力顯然和萬有重力完全不同,這種不同體現在分子間力是一種短程力。比如說典型的London力是距離的六次方反比的。因而普通的均勻氣體是一種穩定的狀態 - 當分子間距離足夠遠,分子間力幾乎為零。而自重力系統中,萬有重力是距離的平方反比的,所以萬有重力是一種長程力,因而星雲就會收縮。
只有當氣體體積足夠小,小到分子間力不再可以忽略時,此時分子間力才成了系統不穩定的源泉。
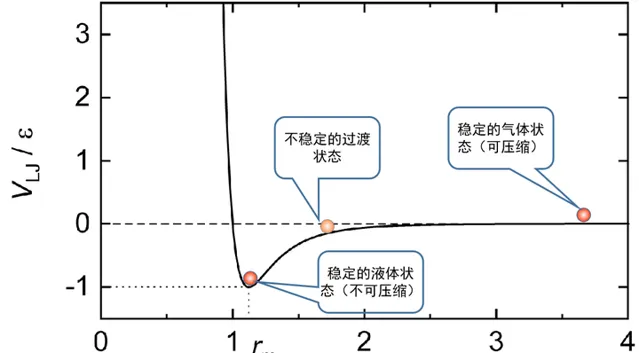
但是,氣液兩相之間的轉換,並不一定會發生這種失穩現象,也就不一定會出現不連續的躍變。在超臨界狀態下,這種變化就是連續的(這就是下文小剛老師的答案中所說的氣液是一相的原因。這個說法不能說錯,但是太潦草了,對沒有接觸過相變理論的人非常容易誤導)。 在超臨界的情況下,由於溫度和壓力都很高,分子間的碰撞就會一直占據主導作用,而分子間的吸重力就不再重要,因此繞過臨界點從氣體過渡到液態是沒有不穩定的過渡態出現的,因此也就沒有相變過程。
液相的穩定存在
上述不穩定的氣液過渡的狀態中,由於 分子間吸重力的存在導致分子聚集狀態直接決定了勢能的變化,導致了負熱容/負膨脹率的產生。 那麽,勢能最低的狀態是什麽呢?顯然,是晶體結構。從氣體的自由分子,到分子開始聚集,再到最終晶體的形成之間,就會一直伴隨著分子勢能的下降。直至最穩定的晶體結構。這就出現了一個問題:
分子的聚集態在氣體和液態之間,為何會出現一個穩定的液相(在液相中分子勢能不變),而不是從氣態直接過渡到固態呢?
一言簡化之,就是液態和固態之間的對稱性是不同的。但是這個情況會比較復雜。
從液態到固態的變化,其密度不會發生顯著變化。也就是說,分子間距的變化很有限。但是一個最大的變化就是,從分子間相對自由的流動變成了 長程的穩固有序排列 。從宏觀上說,就是固體的 剪下模量不再是零 。F. A. Lindemann上世紀初的模型中,假定分子的振動振幅達到分子間距的一定比例時,固體的穩定性就失去了,因此它就開始融化。融化所吸收的熱量於是就保持了固態中的分子振動不會繼續增大。這個模型很簡單,也很有用。但是它並沒有回答這樣一個問題:
液相到底是一種什麽樣的穩定狀態呢?
固態是一個相對容易理解的狀態 - 它是一種有序結構,勢能最低的狀態。在這種狀態下,分子間相互作用力最強,分子的位置就被穩固地束縛起來。但是液態是一種分子間力相對較強,但是有不足以使其形成穩固排列的狀態,情況就非常復雜。可以說直至現在為止,令人滿意的普適理論還沒有出現。因為這個過程中太復雜了,這和具體的 分子構型、分子間相互作用的形式、晶形結構、內部缺陷、表面性質 等一系列復雜問題都息息相關。從液態到固態的變化,單純從單個的分子間的相互作用是不容易解釋的,必須要從 大量分子的長程結構 入手 - 因為固體和液體的最大區別就在於長程的有序結構。
氣液態的區別情況可以簡單地用下圖表示 [1]

因此,固相的形成不是單一的分子之間的相互作用,而是大量分子的協同作用,在這個過程中,某個局部的熱運動漲落就可以輕易地把周邊的有序結構給打破了,而這種局部有序結構的喪失就會像多米諾骨牌一樣引發全域的崩潰。這就使得固相的形成難度比液相更高 - 它需要把熱運動的影響降低到更低的水準。
還是以水為例,像水這種分子極性高並且相互作用復雜的物質,聚集形態會非常復雜。水中的氫鍵存在非常普遍,而氫鍵的形成與分子的形狀、位置、取向息息相關。當每個分子都以最多氫鍵的方式和其他分子結合時,水分子以規則的方式排列,這就是晶體 - 冰。因為氫鍵的強度遠高於一般的分子間力,這種方式的排列,就是勢能最低的情況。
但是在溫度比較高的時候,這種規則排列無法達成,因為水分子不斷振動,打破這些氫鍵。水分子間的 氫鍵就一直在不斷地打破並且不斷地重建過程中 ,這個過程是以飛秒計的。有人說,整體看來在液態水中,大約有12%的氫鍵處於被打破的狀態 [2] 。就是因為這12%的氫鍵斷裂,使得水的整體規整結構被破壞了。 長程的聚集難以持續,但是短程的聚集卻是很容易的 。在液體中,分子間的復雜相互起作用,使得分子會三三兩兩地聚整合團,不斷發生「滑移」。由於分子的不斷碰撞,這些分子團會呈現出聚集-打散-重新聚集的過程。於是乎形成了流動的狀態。 [3]
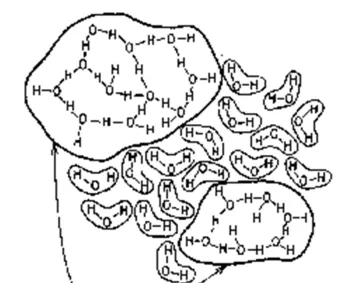
一般說來,液態水中的水分子大約聚集數量在20~200個之間 [4] 。這種局部結構,有規整的,和冰的晶型結構類似,也有不規則的。從某種程度上說,水中的結構在很大程度上和冰沒有本質區別,所差的,只是能否形成長程結構
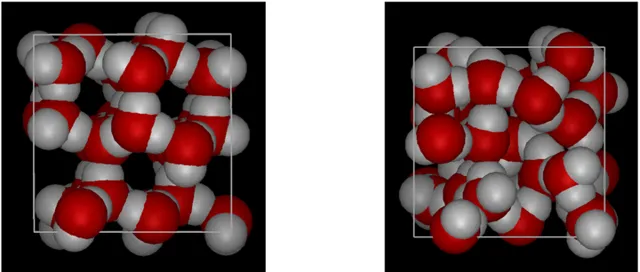
比如說,一種推測的規整分子團的結構是280個水分子的聚集 [5] 。

所以說,人們對固液相變的理解,並不像氣液相變那麽清楚。這裏我仍然定性地用描述一下我的個人理解。
前面提到, 分子間相互作用是一種短程力 。當在液體中,很多分子聚整合團的時候,分子團的尺寸就會比單個分子大得多。相對而言,分子間力就更不容易發生作用。直觀講,較大的分子團接近的時候,其接觸點相比於單個分子要小得多。比如說像上面的水分子團的結構,一個 \left( H_2O \right)_{280} 的分子團所能提供的氫鍵點位要遠少於280個單個的水分子。因此,一旦分子聚整合團,那麽分子間力的影響就顯著下降。
我們前面提到,分子間的相互作用力在氣液相變過程中起到了關鍵作用。它的存在導致氣體向液態過渡的過程中出現了狀態失穩的現象,從而導致了不連續的變化(相變)。而在達到液態的時候,由於分子間作用力的影響,分子局部聚集,從而導致分子間作用力的影響力下降,就導致了它不再繼續聚集,而保持了一段時間的連續變化,這就是穩定的液相的存在。
液固相變
對液態水來說,隨著溫度的繼續降低,分子間作用力的影響又會緩步增加。隨著分子間力的影響增加,分子團之間就會越來越出現互相吸引從而更加聚集的情況。此時,類似前述氣液相變中的不穩定過渡態就又會出現了。
比如說在某個局部,因為一個擾動,分子的聚集程度突然增加了,那麽:
而相反地,這個局部的大規模聚集就必然導致周邊分子聚集程度被打破,同時,由於上述的大規模聚集導致的勢能下降,必然使得周邊分子運動更加劇烈。那麽在周邊:
我們可以看到,前述的大尺度有序結構的形成伴隨著勢能的下降。這就類似氣液過渡態的那種負熱容的情況:當向外傳遞熱量的時候,長程的有序結構形成,從而導致勢能顯著降低。而勢能的降低則會導致動能的增加,使得溫度增加。於是這種過渡態就會崩解為穩定的固態和液態。形成兩相並存的不連續過程。
請註意這是一個非常定性地、簡化地說法。這中間 表面性質 以及 缺陷的性質 起到了極其重要的作用,但是這裏就忽略了。
空間熵和動量熵
從熱力學第二定律的角度,液態結冰的過程可以這樣來看,這是一個是以 空間熵換取動量熵的過程 。
我們可以簡單地將熵歸結為相空間的體積的對數。也就是說,一個系統的熵,取決於兩個方面:它在位置空間中的自由度,以及在動量空間中的自由度。
很顯然,液態在位置空間中的自由度要大於固態。因為液態分子雖然受到束縛,還是可以在較大的空間中移動,而不是只在晶格附近振動。所以說液態有著較高的熵。
隨著溫度的降低,分子的熱運動降低,它的動量空間自由度就會隨之下降。也就是說,它的運動的速度分布變窄了。
固態有著更低的勢能,可以換來更高的動能,進而得到更大的動量自由度。而同時它卻有著更低的位置自由的。總的熵就受到這兩種相反趨勢的支配。當溫度較高的時候,系統選擇更大的位置自由度,從而達成更高的總熵。而當溫度較低的時候,分子已經非常擁擠了, 此時位置自由度的貢獻降低,而動量自由度的貢獻相對更高 。達到一定的低溫後,一部份分子就會自發放棄位置自由度,選擇更加規則的空間排布,釋放出能量來保持另一部份的溫度不再持續下降,從而使得動量自由度維持在較高的水平,換得更高的總熵。從宏觀上看,就表現為一部份液體結冰,從而維持系統的溫度不再下降。在這個過程中,熵減是由位置自由度的壓縮完成的。
假使在降溫的時候液體不結冰,那麽溫度會持續降低,那麽系統的動量自由度會持續下降 - 因而它對總熵的貢獻持續下降。而此時由於分子相對已經很擁擠了,所以位置自由度也不會很高。宏觀上,這就是一種上面腦洞中提到的「果凍」類似的過渡態。這種過渡態比起兩相並存(即犧牲位置自由度換來動量自由度)的熵更低,所以它會自發地變為兩相並存。
如果你對朗道相變理論很熟悉,這種情況就是相變過程中的鞍點情形。從自由能上看,就是隨著系統有序度(coorelation length)的變化,存在 兩個穩定態和一個亞穩態 。
這種情況可以用一個日常生活的例子來說明。比如說我們有一個正方形的盒子,裏面放置著幾根牙簽。我們晃動盒子,會發現牙簽的排列非常雜亂。這是一種典型的熵增。但是當我們放置一把牙簽進去,然後再晃動盒子,我們會發現原來雜亂的牙簽會整齊地排列起來。這看起來變得更加有序了。這是自發熵減了嗎?不是的,因為牙簽的整齊排列,會使得牙簽的運動更加自由。所以它的取向雖然更有序了,卻換來了運動的更大雜亂。
綜上所述,三個典型相態的形成就是這樣的:
自由分子(氣體)\xRightarrow{穩定性喪失} 束縛分子(液態)\xRightarrow{穩定性喪失} 長程有序束縛分子(固態)
補充公式版:相變的一般熱力學描述
從熱力學上講,自由能最低的狀態是最穩定的存在狀態。從吉布士方程式看:
dG=Vdp-SdT
在等壓過程種,由於熵總是正值,所以自由能總是隨著溫度的增加而減小。並且,由於
S_g>S_l>S_s
所以定性看,氣液固的自由能隨溫度的變化如下:
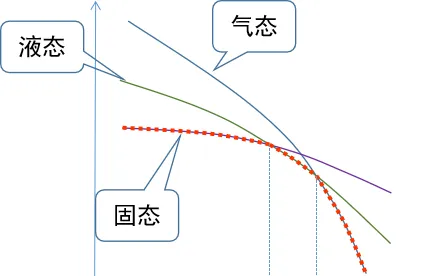
因此隨著溫度的降低,物態就會從氣態變成液態再變成固態。當氣液自由能相等的時候,就是沸點,液固自由能相等的時候,就是熔點。
由於
G=H-TS
所以,由於兩個相態之間的熵值不連續,則必然會出現相變過程中的不連續,表現為潛熱的存在、密度的變化等。
補充公式2:典型的穩定性準則
這裏我們推導一下相態的穩定性準則。
對一個孤立系統,在一個平衡態,我們有:
S=S_{eq}
這個平衡態必須有兩個特征,第一,它的熵最大,第二,它是穩定的。
熵最大這個很容易理解,因為這是熱力學第二定律的直接結論。它是穩定的,意味著對任何擾動,它是負反饋的,也就是說,它會自發地返回到平衡態。
我們假設一個系統。這個系統中一個局部發生了一點點擾動(比如說溫度變化了一個 \delta T ),那麽這點擾動會引起系統如何變化呢?
我們把這個系統分成兩個子系統:發生擾動的那個小局部為子系統1,剩余的為子系統2。那麽我們有:
S=S_1+S_2
對於這個擾動,我們可以計算它帶來的熵變:
\Delta S=S-S_{eq}=\left( \frac{\partial S_1}{\partial U_1} \right)\delta U_1+\left( \frac{\partial S_2}{\partial U_2} \right)\delta U_2+\left( \frac{\partial^2 S_1}{\partial U_1^2} \right)\frac{\left( \delta U_1 \right)^2}{2}+\left( \frac{\partial^2 S_2}{\partial U_2^2} \right)\frac{\left( \delta U_2 \right)^2}{2}+...
由熱力學基本公式我們知道
\left( \frac{\partial S}{\partial U} \right)=\frac{1}{T}
所以:
\Delta S=\left( \frac{1}{T_1}-\frac{1}{T_2} \right)\delta U+\left( \frac{\partial}{\partial U_1}\frac{1}{T_1}+\frac{\partial}{\partial U_2}\frac{1}{T_2} \right)\frac{\delta U^2}{2}
請註意,上式中用到了孤立系統能量守恒的條件,也就是:
\delta U_1=-\delta U_2\equiv\delta U
由於 \delta T 為無窮小量,所以上式中第一項為零。而對於第二項中,我們有:
\frac{\partial}{\partial U}\frac{1}{T}=-\frac{1}{T^2}\frac{\partial T}{\partial U}=-\frac{1}{T^2}\frac{1}{C_V}
所以,第二項就變成了:
\frac{1}{2}\delta^2S=-\frac{C_{V1}}{2T^2}\left( 1+\frac{C_{V1}}{C_{V2}} \right)\left( \delta T \right)^2
由於子系統1遠遠小於子系統2,所以,
\frac{1}{2}\delta^2S=-\frac{C_{V1}}{2T^2}\left( \delta T \right)^2
由於平衡態中熵處於最大值,所以,任何的擾動都只能使得熵減少。因而,我們有:
\delta^2S=-\frac{C_{V1}}{T^2}\left( \delta T \right)^2<0
因此,我們得到了 相態穩定的條件,就是它的比熱必須大於零 。
同理,我們可以假設一個壓力的擾動,這樣我們會得到另外一個條件:
\delta^2S=-\frac{1}{TV k_T}\left( \delta V \right)^2<0
也就是說, 相態穩定的另一個條件就是,它的壓縮率必須大於零。
參考
- ^ doi:10.1063/1.4818747
- ^ Cho et al 1997, Suresh et al 2000
- ^ https://doi.org/10.1039/DF9572400133
- ^ Turi et al. Science 2005
- ^ Martin Chaplin 2000











