在今年的搞笑諾貝爾獎上,在眾多獲獎研究一片和睦的氛圍中,有這麽兩項獎項「懟」上了。
物理學獎:為什麽行人不會碰撞?
動力學獎:為什麽行人會碰撞?
行人:你們禮貌嗎?

行人既不是質點也不是什麽斜坡上的滾軸,下一步會往哪個方向走可能行人自己都不知道,又怎麽對行人的運動進行研究?難道研究人員都是心理學大師?
當然沒這麽復雜,早在上世紀30年代就有科學家開始了對 行人集群運動 (Pedestrian Collective Motion)的研究,到今天已經有專門的一門學科來研究這一現象—— 行人動力學 (Pedestrian Dynamics)。
今天小編就帶大家看一下,怎樣利用建模去分析行人的復雜運動。
01 建模的思想,在一只雞中
【生活大爆炸】裏有這樣一個關於「真空中的球形雞」的笑話:
一個農夫找上了物理學家,要求物理學家解決農場的雞不下蛋的問題。物理學家經過計算之後告訴農夫,我找到了解決問題的方法,但這個方法只對在真空中的球形的雞有效。

雖然這個笑話本意只是吐槽物理學家,但「球形雞」精神在物理學研究中有著重要意義: 忽略事物一部份微觀特征,將復雜問題簡化 。
高中物理課上學到第一個重要概念——質點,其實就是「球形雞」精神的一種套用。
02 把行人變成「真空中的球形人」
類似「球形雞」問題,行人有手有腳,形狀不規則,全身各個部位有著不同的運動方式。為了簡化問題,我們在研究時,首先要將行人轉變成一個方便研究的「粒子」。
最簡單的簡化,就是假設行人所在的空間是一個位於真空中的球。
行人問題只需要研究平面運動,球退化為圓。
要研究行人的運動,只需要研究這些圓在一定條件下的運動情況就可以了。一群人的行為不好模擬,但是一群二維粒子的運動模擬屬實是非常熟悉了,計算物理中的 分子動力學模擬 就是。
當然,這種簡化實在太過簡單,就像「球形雞」那樣忽略了太多的細節,模擬結果可能會與實際有很大差距。比如各大景區的一線天,窄的地方現實中遊客可以側身透過,但在半徑為遊客肩寬的球形模擬中遊客無法透過。
為了讓模擬結果更貼合實際,我們可以根據研究的主要物件在上述的圓球模型上進行修改。例如研究需要考慮行 人以自身為軸的轉向運動 ,我們就可以將圓修正為套著球形的橢圓,用橢圓的長軸來體現行人的肩寬,短軸方向就是行人的朝向。
除了形狀,在動力學模擬中,還需要考慮粒子之間相互作用的規則。這個規則來源於行人運動規律的總結,比如: 行人之間總是會保持一個舒服的距離,並且會盡量避免碰撞 。
在兩人離得很近時,為了保持舒服的距離,行人會自發遠離,表現為在一定距離之內,行人會受到對方的作用而改變運動狀態,這一距離就是 最短作用距離 d_m 。
在兩人離得很遠時,對方從遠處迎面走來,行人會根據彼此的橫向距離判斷是否會發生碰撞,當橫向距離小於一定數值時,行人就會提前改變自己的運動狀態來避免碰撞,這一數值就是 最短橫向作用距離 d_{y,m} 。
實際上,舒服的距離要大於會發生碰撞的距離,也就是 d_m > d_{y,m} 。
在之前的橢圓模型上加上行人的 受影響區域 α,如下圖所示:
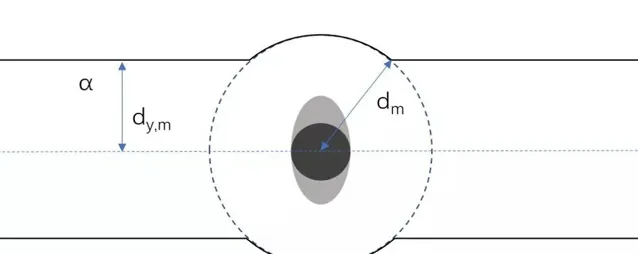
這樣我們便將一個不規則難模擬的行人轉變成了一個 簡單的、有著一定受影響區域的粒子 。
03 再加上力
現在我們將模擬物件簡化成了簡單的粒子,那麽是什麽改變了粒子的運動狀態呢?
Helbing認為,行人運動狀態的改變是由於受到外力驅動而變化,這個力就是 社會力 (Social Force),在社會力作用下的行人運動模型叫做 社會力模型 。社會力並不是像什麽重力、壓力、彈力那樣真實存在的力,而是描述 導致行人運動狀態發生改變的一種作用 。社會力模型的基本解析方程式為:
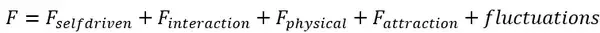
其中, Fselfdriven 為行人所受到的自驅動力, Finteraction 為行人間的相互作用力, Fphysical 為行人所處環境中障礙物對行人所施加的作用力, Fattraction 為特殊位置的吸重力, fluctuations 是雜訊項。
在社會力模型中,行人的座標r、時間t都是連續的。在給定初始條件之後,透過上述的基本解析方程式,就可以模擬出之後任意時刻的行人運動狀態。
04 行人為什麽不會碰撞?
那麽回歸最開始的話題,行人之間是怎樣避免碰撞的呢?
Corbetta等人便利用了我們在第二部份和第三部份提到的模型來研究這一問題。
考慮兩行人p1、p2避免碰撞的事例,(行人密度足夠稀疏可以忽略第三人的作用,)這一事例滿足的動力學方程式組為:
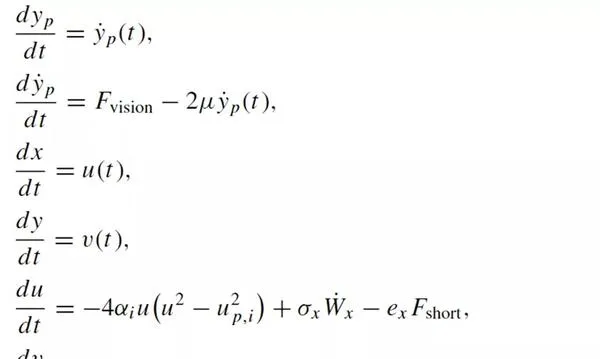
其中,x、y分別為沿著行人前進方向和垂直於行人前進方向的縱向和橫向座標;u、v分別為縱向和橫向速度;α、β是正的模型參數; \sigma_x\dot{W}_x 、 \sigma_y\dot{W}_y 分別是縱向和橫向的高斯雜訊項; F_{short} 是短程避免碰撞的力, F_{vision} 是長程基於視野判斷的力,這兩個力分別就對應了在第二部份提到的兩種相互作用。
這麽多參數小夥伴們可能和小編一樣開始頭疼了。

但是沒有關系,我們並不需要去真正利用這個方程式組做計算,我們只需要去理解方程式組描述的物理過程就好了。
社會力模型其實是 基於牛頓第二定律對行人運動過程進行描述 ,我們所看到的方程式其實只是比牛二律復雜了億點點。

雖然多了很多參數,這個方程式組同牛頓第二定律一樣,描述的是 行人受到的社會力與行人速度變化的關系 ,速度影響的是行人的未來路徑,也就是說, 行人透過改變自己未來的路徑來避免碰撞 。
下面考慮兩行人A、B在一走廊相向而行的具體情況。
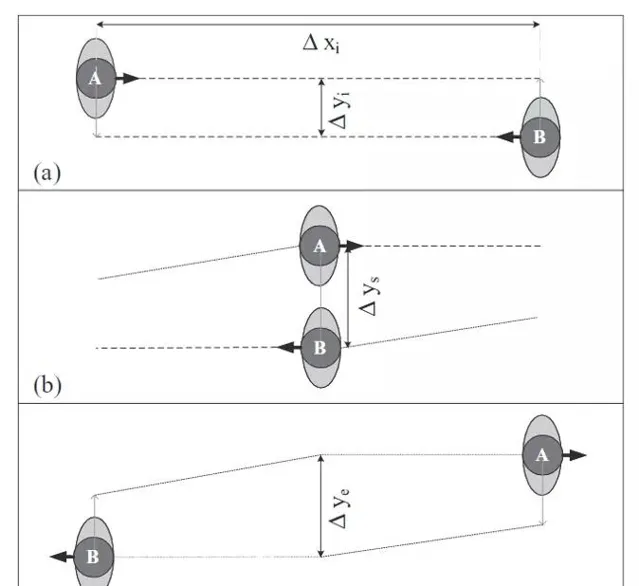
A、B具有初始橫向間距 Δy_i ,當兩人肩並肩時,有並列橫向間距 Δy_s , Δy_s 如果小於兩人肩並肩的寬度,就會發生碰撞。
不同初始橫向間距對應的並列橫向間距關系如下圖:
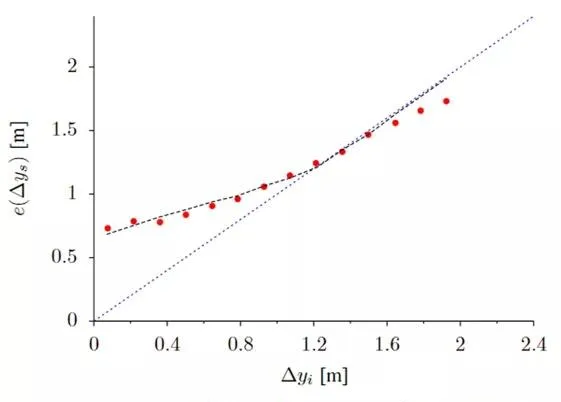
其中黑色虛線是數據模擬結果,紅點是從9089例避免碰撞的案例中得到的數據,藍色虛線是在橫向速度為0,即行人沒有避讓動作下的結果。我們可以看到模擬效果非常好,結果與實際十分接近。
當初始橫向間距為0時,並列橫向間距為0.75m;初始橫向間距小於1.4m之後,並列橫向間距大於初始橫向間距。
因此,行人避免碰撞的原理是: 當兩行人的初始橫向間距小於1.4m時,行人會透過橫向移動,改變自己的預期路徑,擴大彼此之間的間距,並保證在肩並肩時,彼此的間距至少為0.75m。
另外,該團隊還統計並模擬了一些行人相關的數據:行人最喜歡以1.29m/s的速度行動,部份跑動的行人速度常見為2m/s;行人在移動時會以路中心進行橫向的波動,橫向移動速度和距離都呈現高斯分布,峰值均出現在0處。
05 行人為什麽會碰撞?
之前提到過,在社會力模型中,在影響行人下一步移動的因素中,決定性因素的是 速度 , 預判 在行人避免碰撞的移動中起了重要作用。
行人透過預判避免彼此碰撞,自然發生碰撞便是因為其他因素導致了預判失敗。
Hisashi Murakami等人透過實驗證明了這一點。
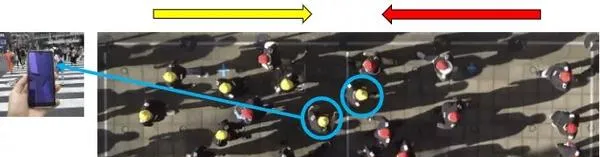
在實驗中,眾多被試分成兩組,相向而行,其中一部份實驗者被要求邊玩手機邊進行移動,實驗者負責統計突然轉身(Suddenness of turns)發生的次數以及突然程度。

結果可想而知,玩手機的人突然轉身的次數和突然程度都要遠高於其他人。玩手機這一行為分散了行人的註意力, 降低了個人的預期能力,導致行人需要在更短的時間內做出變向來避免碰撞 。
另外有意思的是,在玩手機的人對向與周圍的行人突然轉身次數和突然程度也都有所上升,這說明玩手機 不止會降低自己的判斷力,還會影響其他路人的判斷能力 。
正所謂行路不規範,親人兩行淚。各位小夥伴們在走路的時候還是要專心啊,可千萬別成為別人的研究案例哦~
06 一些拓展
在日常生活中,我們也可以利用「真空中的球形雞」思想去分析一些其他的常見問題。
比如在坐車時會遇到的, 前方明明沒有什麽意外事故,卻莫名其妙發生了堵車 ,也就是「 幽靈堵車 」問題。
我們可以直接利用社會力模型來對這種現象進行分析:汽車行車時會有一個安全距離,當兩車距離小於安全距離時,後車就要進行減速,表現為 前後車輛之間有一個排斥力 。當車流量密度很大時,車輛間距被壓縮到了最小,也就是安全距離;這時如果前車突然減速,後車被迫要減速到更慢速度來恢復安全距離,這一減速行為直接導致後後車更大的減速。這樣減速振幅遞增,直到在某輛車之後全部靜止,發生「幽靈堵車」。
在密集人群,特別是長佇列中,會出現與「幽靈堵車」類似現象——一部份前進而另一部份人靜止的「 走停波 」。「走停波」產生的原因與「幽靈堵車」也是一樣的,即密集人群中的減速導致的靜止。
從模擬角度來看,行人與車輛在研究時都被模擬成了「真空中的球形」,並且受力情況相同,兩者在模型研究中無本質區別,自然也會在相同情況下(密集車輛或人群)產生相類似的現象(「幽靈堵車」與「走停波」)。
在諸如月台、購票機以及景區入口等地方,行人有時會自發排成佇列。

這種自發排隊當然是因為大家都很講文明啦!

咳咳,講文明確實是一方面,我們還可以從另一方面,利用社會力模型來看行人自發排隊的原因。
我們知道,當粒子受到外力時,會具有一定的勢能,並且能量越低的結構越穩定。
在社會力作用下,我們可以認為行人也會有一定的 社會勢能 ,行人自發排隊是因為,與雜亂無序的分布相比,在佇列這種有序結構下,人群總的社會勢能更低。 能量低的結構相對更加穩定 ,所以人群會自發排成佇列,就好像物質微粒自發排列形成穩定的晶體結構一樣。
雖然我們沒有更進一步地去做動力學模擬,但透過建模方法對問題進行 定性 分析,我們依然可以嘗試給出問題的答案,對問題有更深入的理解~
(那麽如果給考試試卷做一個建模,是不是就可以直接得到考試答案了?小編妄想ing)
參考資料:
- Corbetta, A., Meeusen, J. A., Lee, C., Benzi, R., & Toschi, F. (2018). Physics-based modeling and data representation of pairwise interactions among pedestrians. Physical Review E, 98(6), [062310].https:// doi.org/10.1103/PhysRev E.98.062310 .
- Murakami H, Feliciani C, Nishiyama Y, Nishinari K. Mutual anticipation can contribute to self-organization in human crowds. Sci Adv. 2021 Mar 17;7(12):eabe7758. doi: 10.1126/sciadv.abe7758. PMID: 33731351; PMCID: PMC7968841.
- 龔曉嵐,魏中華.行人動力學的研究進展[J].人類工效學,2008(02):68-71+73.
- 程漢. 行人集群運動演化過程中的動力學機理研究[D].中國科學技術大學,2020.DOI:10.27517/d.cnki.gzkju.2020.000364.
- Guo Wei, Wang Xiaolu, Xiaoping Zheng. (2015). Lane formation in pedestrian counterflows driven by a potential field considering following and avoidance behaviours. Physica A: Statistical Mechanics and its Applications. 432. 10.1016/j.physa.2015.03.020.











