以下討論比較trivial,給與我同是初學者的人來看看。
定義範疇等價的動機在於,如何更好地刻畫兩個範疇是「一樣的」這個概念。範疇同構太強了,需要函子 F:\mathcal{C}\to \mathcal{D} 與 G:\mathcal{D}\to \mathcal{C} 的復合必須分別 等於 \mathcal{C} 與 \mathcal{D} 上的恒等函子,而範疇等價只需要分別 自然同構於 \mathcal{C} 與 \mathcal{D} 上的恒等函子。
這個條件放寬會帶來什麽差異呢?可以證明, F:\mathcal{C}\to\mathcal{D} 是範疇同構若且唯若:
- full: 對任意 A,B\in \text{Obj}(\mathcal{C}) , \text{Hom}_\mathcal{C}(A,B)\to \text{Hom}_\mathcal{D}(FA,FB) 是滿射
- faithful: 對任意 A,B\in \text{Obj}(\mathcal{C}) , \text{Hom}_\mathcal{C}(A,B)\to \text{Hom}_\mathcal{D}(FA,FB) 是單射
- surjective: 對任意 D\in \text{Obj}(\mathcal{D}) ,存在 C\in \text{Obj}(\mathcal{C}) 使得 F(C) 等於 D
- injective: 如果 A,B\in \text{Obj}(\mathcal{C}) 使得 F(A)=F(B) ,則 A=B
而 F:\mathcal{C}\to\mathcal{D} 是範疇等價若且唯若:
- full: 對任意 A,B\in \text{Obj}(\mathcal{C}) , \text{Hom}_\mathcal{C}(A,B)\to \text{Hom}_\mathcal{D}(FA,FB) 是滿射
- faithful: 對任意 A,B\in \text{Obj}(\mathcal{C}) , \text{Hom}_\mathcal{C}(A,B)\to \text{Hom}_\mathcal{D}(FA,FB) 是單射
- essentially surjective: 對任意 D\in \text{Obj}(\mathcal{D}) ,存在 C\in \text{Obj}(\mathcal{C}) 使得 F(C) 同構於 D
由此我們可以看到,範疇同構與範疇等價的區別完全在於後面對object的限制條件:範疇同構需要both surjective and injective,而範疇等價僅僅需要essentially surjective就好了。
這就告訴我們,假如說我們有範疇同構(當然同時也是範疇等價),如下圖所示:
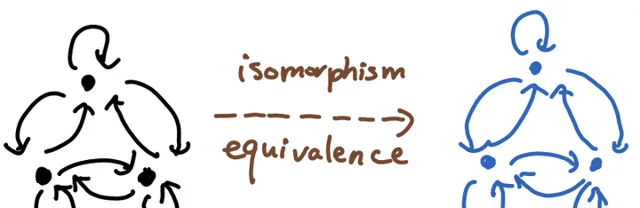
我們只需要在右面的範疇(藍色)再添加一些object(下圖橙色點),使得新的object同構於某些舊的object,就可使得這兩個範疇不再同構,但仍然保持範疇等價,因為剛才添加新的object的這個操作仍然保持essentially surjective

換句話說,我們只需要同構地copy許多份object,就會破壞範疇同構但仍然保持範疇等價。
這也解釋了為什麽相比範疇同構,我們還需要範疇等價:因為我們希望允許隨意地copy許多份object,反正copy過後本質上結構沒有發生變化。
文小剛老師居然點贊了,受寵若驚。











