特定情形下,三體問題是可解的,甚至某些特解非常簡單。但是一般而言,三體問題不存在解析通解,即,我們無法用代數運算式寫出任意構型下三體問題的通解。
二體問題的約化
要了解三體問題,首先可以從二體問題開始。
二體問題,顧名思義,研究的是兩個物體在彼此相互作用下的運動,例如只考慮地球和月亮在彼此萬有重力下的運動,就可以抽象為一個二體問題。將兩個天體看作質點,設其質素分別為 m_1 和 m_2 ,初始位置分別為 \vec r_1 和 \vec r_2 ,初始速度分別為 \vec v_1 和 \vec v_2 ,根據牛頓運動定律,可以得到:
\vec F_{12}=m_1 r_1''
\vec F_{21}=m_2 r_2''
到此,我們寫出了二體問題遵循的運動方程式,剩下的問題便是解這組方程式了。
使用高中物理中常用的質心的概念,可以將二體問題分解為質心的運動和兩個天體相對於質心的運動。
質心的位置為: r_心=(m_1\vec r_1+m_2\vec r_2)/(m_1+m_2)
質心的運動是一個單體問題,而在質心座標系下,兩個天體對於質心的運動可以用兩個天體之間的相對位移來描述,即
r_{相對}=\vec r_1-\vec r_2
r''_{相對}=(1/m_1+1/m_2)F_{12}
此處又變成了一個單體問題。所以,二體問題本質上可以理解為兩個獨立的單體問題的結合,分別求解這兩個單體問題即可得到二體問題的解。
由於求解單體問題是比較容易的,因此二體問題作為可解問題,遠遠不如「表哥」三體問題名氣大了。
三體問題溯源
時間回到1885年,學數學出身的瑞典國王奧斯卡二世贊助了一場有獎數學競賽,競賽的題目是4個數學難題,其中之一便是多體問題——求解太陽系的運動問題。
這一難題從牛頓時代提出直到競賽釋出之時,在學術界始終無人能攻克。眾多數學物理大師先後折戟沈沙鎩羽而歸,甚至牛頓力學的奠基人牛頓本人,也只能寫出其運動方程式,然後在求解的過程中失去信心,認為這是「人類智力不可勝任的任務」。

面對被牛頓認為達到了人類不可解這種級別的難題,剛剛而立之年的龐加萊並沒有退縮,他把問題進行了一些簡化,只考慮三個星體,歸納為著名的「三體問題」。此後龐加萊奮筆疾書,在比賽送出的論文裏發明了一種方法,可以求解任意精度的三體運動軌跡。
不久,賽事方接收了龐加萊的論文,審閱之後認可了他的解答,並給他發了比賽獎金,之後著手把這篇「曠世奇文」刊登在學術期刊上。就在這時,龐加萊發現,自己的解答錯了。這下子事情就比較尷尬了。

龐加萊不得不支付了召回雜誌等一系列補救措施的費用,雖然獎金並沒有被收回,但是最後算下來,龐加萊還是虧了不少小錢錢的。

雖然參加比賽贏了獎金卻虧了更多錢,但龐加萊還是在這個過程中收獲了很多東西,比如,他提出了相圖理論,並最終開創了混沌這一數學分支。龐加萊發現,一般性的三體問題往往是混沌的,即,如果兩個三體系統的初始條件即使僅有一點點微小的不同,在後續的演化過程中,兩個系統的動力學狀態會產生巨大的不同。
混沌系統是確定的,例如三體系統的運動方程式是可以用牛頓力學精確寫出來的,三體問題在動力學上是確定的,沒有隨機性。但是混沌系統是不可預測的,因為初始條件的一點微小差別,會導致其之後運動狀態的巨大不同,演化時間的增加會放大初值的微小擾動,導致我們無法判斷其長期的軌跡。
這一切仿佛上帝開的一個天大的玩笑:我們可以寫出它的方程式,給定一個初始條件,我們甚至知道它的軌跡是確定的,但我們還是無法預測。
就像一座山,山就在那裏,但觸不可及,撩撥著探索者的心弦。
代數不可解與數值不穩定
三體問題的「不可解」體現在幾個方面:
1、對於一般性的三體問題,無法寫出一個解析通解。
我們沒辦法找到一個類似單體問題通解那樣的數學運算式來描述三體問題。可能有小夥伴會問,是不是隨著數學的發展,人們就能找到這樣的代數運算式呢?
其實也是不可以的。在二體問題的分析中,我們已經知道,在三維空間有x,y,z 3個自由度,因此每一個天體可以寫出3個二階微分方程式,如果覆寫成一階微分方程式,那就是6個。對於三體問題,就會得到18個一階微分方程式。求解三體問題,等價於解這個18個一階微分方程式構成的復雜的方程式組。1941年,西格爾從數學上證明了,不可能找全這18個代數積分。所以,代數角度求積分來解三體問題的道路,已經被證明完全不通了。

2、對三體問題的數值解,會面臨混沌的初值敏感問題。
既然直接代數積分找解析解行不通,那麽為什麽不用強大的超級電腦來求數值解呢?在很多領域,只要數值解精度足夠,是可以勝任解析解的任務的。
雖然人們透過電腦來試圖「開掛」,但是三體問題更狡猾,它是混沌的!
混沌系統的一大特點便是對初值敏感,如果給電腦的初始條件有一點小小的誤差,例如我們想研究B612星球、賽博坦星球和奧特之星構成的三體問題,如果在輸入程式的初始條件時,迪迦的戰鬥光線影響了天文望遠鏡對奧特之星速度的觀測,導致了一個小小的誤差,之後在經過一段時間的電腦模擬演化後,很可能算出一個和現實偏差巨大的結果,俗話說便是,「失之毫厘,謬以千裏」。

於是一些小夥伴有疑惑了,如果我換用更精確的數值積分方法是不是就可以了呢?歐拉方法只取一階不夠精確,我換三階龍格庫塔法,甚至四階龍格庫塔法,不行再用更高級的積分方法......
很遺憾,並不是這樣的。三體問題在數值上是「病態的」,即問題對初值敏感,就像「蝴蝶效應」一樣,蝴蝶扇動翅膀的微擾都有可能造成一場龍卷風級別的計算偏差。病態問題是其數學上內稟的性質決定的,和計算方法無關,換積分演算法並不能解決計算的不穩定性問題。
特解
一般的三體問題是沒有解析通解的,但這不妨礙在某些特定構型下,三體問題有解析解,甚至是非常直觀而簡單的解析解。為什麽呢?因為特解要求初始條件具有某些限制條件,例如保持一定的對稱性,或者初速度具有某種規律。這些條件其實是對一般性三體問題的約束,增加約束可以減少問題的自由度,當自由度足夠少,便可以解析求解了。
第一種存在特解的情況便是,把三星擺在一條直線上,然後讓兩邊的星體圍繞中間的星體做圓周運動。
其次可以把三星擺在等邊三角形的三個頂點上,讓它們圍繞三角形中心做圓周運動。
稍復雜一點的構型是將它們擺在8字型軌域上,也可以使用解析運算式對其運動進行描述,如下圖:
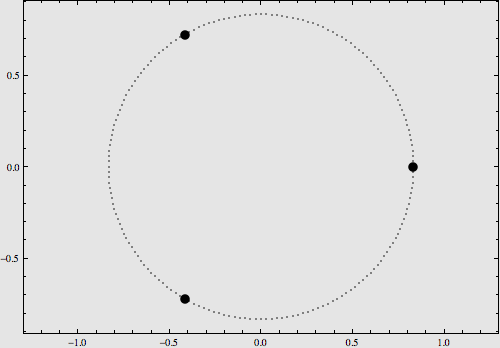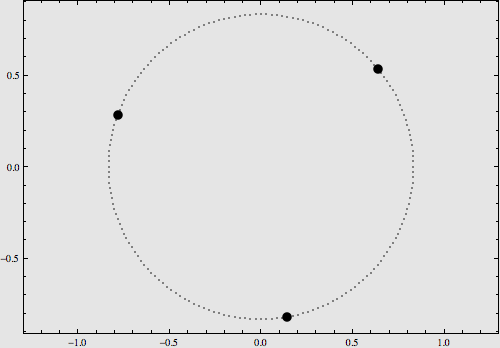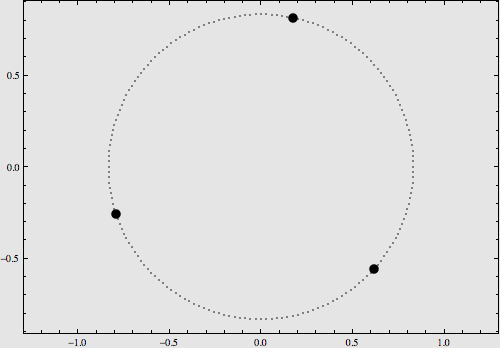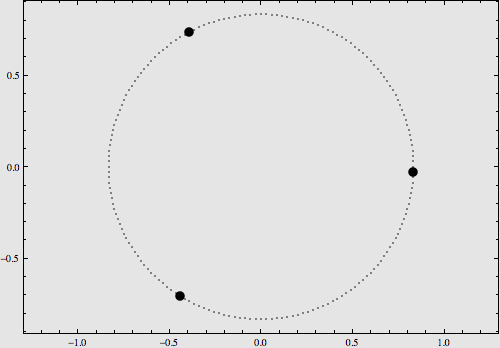
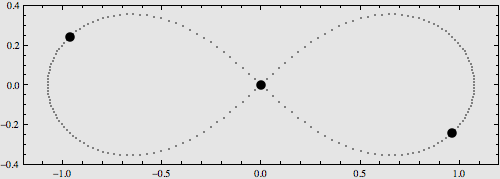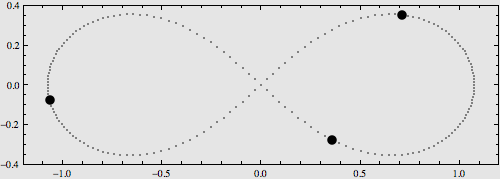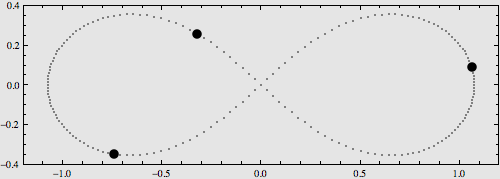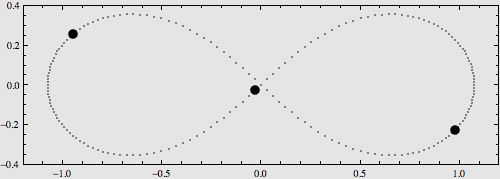
更多的特解不再一一列舉。
三體問題是混沌的,對於其短期內的動力學軌跡,我們可以使用數值方法進行模擬,甚至可以達到非常高的精度。但是對於其長期的動力學軌跡,解析解已經不奢望了,數值解也只能參考參考,就像第二天的天氣預報往往很準確,但是15天後的天氣預報往往只能參考參考。也許,螢幕前的你打了個哈欠,就能影響地球某個地方未來的天氣呢~











