袁讲经典18:以一道变速圆周运动题目为例讲两个知识点
真的好久没有更新了,最近在探索做视频直播,失败了!
我们继续文字分享吧!
例1: 如下图所示,在竖直平面内,轻绳a和轻绳b悬挂一质量为 m 的小球处于静止状态,其中轻绳a为水平,轻绳b与竖直方向角度为 \theta ,现在剪断轻绳a的瞬间,求轻绳b的拉力大小和小球的加速度大小。
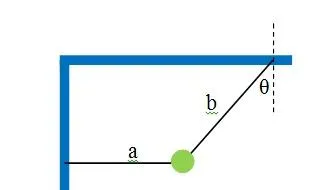
解: 这道题是一道变速圆周运动问题,那么变速圆周运动又有哪些公式可以用呢?
我们看一下匀速圆周运动的公式,如下,
F_n=m\frac{v^2}{r}=m\omega^2 r=m(\frac{2π}{T})^2r ,
那么这个公式在变速圆周运动中是否还可以使用呢?
首先, F_n=m(\frac{2π}{T})^2r 肯定不能用了,因为周期是个平均概念,变速圆周运动中速度、角速度时刻在变化,所以该公式无法使用,
而 F_n=m\frac{v^2}{r}=m\omega^2 r 公式依然可以使用, 但是使用时要注意:
1.要采用瞬时速度大小和瞬时角速度大小,瞬时速度和瞬时角速度之间的关系依然满足 v=\omega r ,但我们高中一般很少用到瞬时角速度,所以一般采用 F_n=m\frac{v^2}{r} 公式。
2.注意该公式中的 F_n 并不是合力,只是指向圆心方向(法向)的力,至于切向方向的力也依然满足牛顿第二定律,
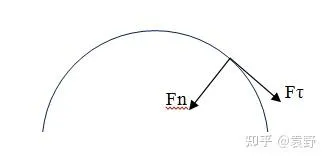
如上满足,
F_n=ma_n=m\frac{v^2}{r} , F_τ=ma_τ ,
其中 a_n 和 a_τ 分别称为法向加速度和切向加速度,
那么合加速度为, a=\sqrt{a_n^2+a_τ^2} 。
好了,我们回到上面这道题目,剪断轻绳a的瞬间受力分析如下,
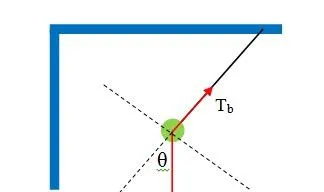
因为接下来小球是做变速圆周运动,所以我们要在法向和切向进行力的分解,
法向, T_b-mg\cos\theta=ma_n=m\frac{v^2}{r} ,其中剪断瞬间 v=0 ,
切向, mg\sin\theta=ma_τ ,
解得, T_b=mg\cos\theta , a_n=0 , a_\tau=g\sin\theta ,
所以, a=\sqrt{a_n^2+a_τ^2}=a_\tau=g\sin\theta ,
即,轻绳b的拉力大小为 T_b=mg\cos\theta ,小球的加速度大小为 a=g\sin\theta 。
好了,做完了,这就是关于变速圆周运动题目的做法。
下面留一个问题,第一个留言且回答正确的小伙伴们私信作者获取10元购书券一张(仅可用于购买袁野老师的物理辅导书)
例2: 上题中,现在剪断轻绳b的瞬间,求轻绳a的拉力大小和小球的加速度大小。
好了,小伙伴们抓紧留言吧。
我们接着往下说,在上题中,在还没有剪断轻绳前,我们计算两根轻绳的拉力大小,特别简单吧,得到, T_{a0}=mg\tan\theta , T_{b0}=\frac{mg}{\cos\theta} ,
然后我们对比 T_{b0} 和 T_b 发现,绳子的拉力存在突变。
但是我们在做上面这道题目的时候, 根本不关心剪断前绳子的拉力大小!
这就是关于绳子瞬态问题的解法,叫做,
绳子看后!
但如果是弹簧,就不一样了。叫做,
弹簧看前!
为什么呢?
绳子和弹簧的拉力都是因为发生弹性形变产生的,但绳子的弹性形变肉眼不可见,易突变,弹簧的弹性形变肉眼可见,很大,恢复需要时间!
好了,然后,我们将上题改编为,
例3: 如下图所示,在竖直平面内,轻弹簧a和轻弹簧b悬挂一质量为 m 的小球处于静止状态,其中轻弹簧a为水平,轻弹簧b于竖直方向角度为 \theta ,现在剪断轻弹簧a的瞬间,求轻弹簧b的拉力大小和小球的加速度大小。
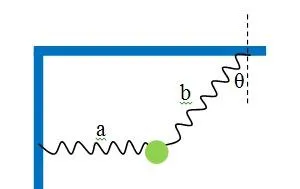
解: 首先说一说轻弹簧a的情况,因为剪断了,所以不用考虑了,
当然很多小伙伴对这个都有疑问,认为剪断的瞬间不是还保持拉长的形变么,怎么就不考虑了呢,
因为我也没有说明在哪里剪断,你可以认为在靠近小球的附近剪断不就可以了吗!当然这样想比较牵强,而本质是因为轻弹簧的「轻」,「轻」就是不考虑质量,就是没有质量,没有质量的物体在高中物理中必须受力平衡,否则根据牛顿第二定律将产生无穷大的加速度,也就是说轻弹簧不存在一端受力的情况,即轻弹簧不存在如下受力情况,
这就是模型限制,没必要深究,如果非要说现实中是可以这样一端受力的呀,那现实中弹簧有质量的呀,如果告诉你弹簧质量,或许可以算一算。
好了,现在我们就当做剪断的弹簧就没啥用了。
那么这道题目怎么做呢?
记住弹簧看前!
所以,我们计算没有剪断前两弹簧的弹力大小分别为,
T_{a0}=mg\tan\theta , T_{b0}=\frac{mg}{\cos\theta} ,
剪断瞬间, T_{a}=0 , T_{b}=T_{b0}=\frac{mg}{\cos\theta} ,
所以此时,弹簧b的拉力大小不变,重力不变,所以,
\vec {mg}+\vec {T_{b}}=-\vec{T_{a0}} (矢量计算)
也就得到此时小球的加速度大小为, a=\frac{T_{a0}}{m}=g\tan\theta ,
好了,这样就做完了,我们根本不关心剪断后小球做什么运动,事实上我们也很难分析剪断后小球复杂的曲线运动是什么样的。
好了,今天这道题目,我们至少学到了两点:
1.变速圆周运动向心力公式怎么用!
2.瞬态问题,绳子看后,弹簧看前!
小伙伴们,咱们下期再见啦!










