高赞说的没错
本质上就是圆的外切正六边形的面积
S_{1}=6\cdot\frac{1}{2}\cdot\frac{2\sqrt{3}}{3}r^{2}=2\sqrt{3}r^{2}
和内接正八边形的面积
S_{2}=8\cdot\frac{1}{2}r^{2}\sin\frac{\pi}{4}=2\sqrt{2}r^{2}
的平均值
实际上,在数学史中,利用圆的内接或外切正多边形的周长或面积,去逼近圆的周长或面积,是早期数学家们的常规思路,举两个例子:
考虑一个数列问题:
数列 \left\{ a_{n} \right\} 、 \left\{ b_{n} \right\} ,满足 a_{1}=2\sqrt{3} , b_{1}=3 , a_{n+1}=\frac{2a_{n}b_{n}}{a_{n}+b_{n}} , b_{n+1}=\sqrt{a_{n+1}b_{n}} .
求数列 \left\{ a_{n} \right\} 、 \left\{ b_{n} \right\} 的通项公式.
这实际上是2200多年前,古希腊数学家阿基米德使用的割圆术
他本质上使用圆的外切正 3\cdot2^{n} 边形的周长,以及内接正 3\cdot2^{n} 边形的周长,去逼近圆周长
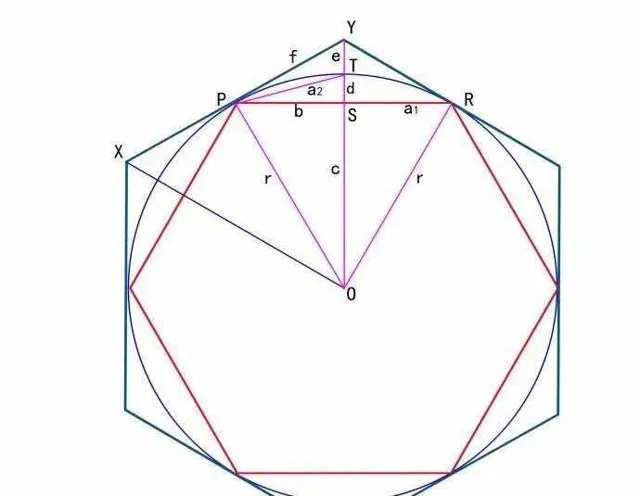
而 a_{n} 和 b_{n} 的几何意义,分别是圆的外切正 3\cdot2^{n} 边形的周长与圆直径的比值,以及内接正 3\cdot2^{n} 边形的周长与圆直径的比值
详见:
而刘徽则使用了另一种方法:
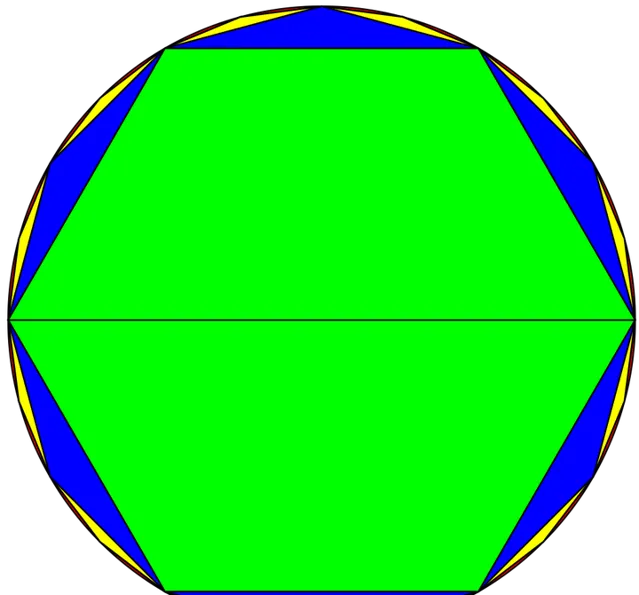
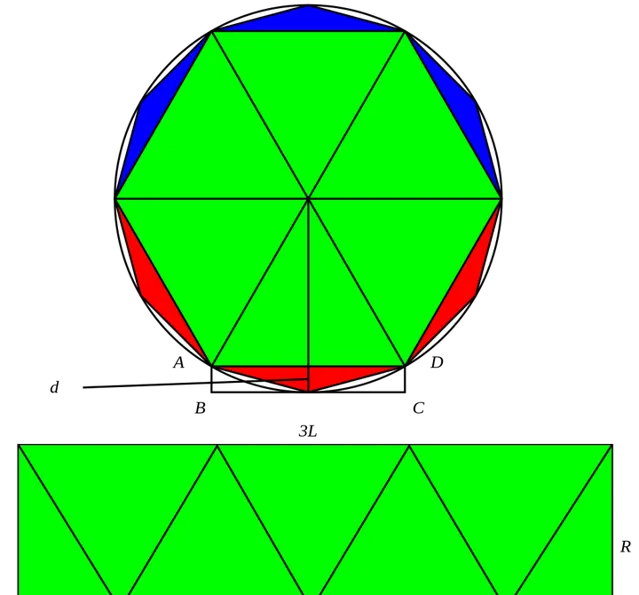
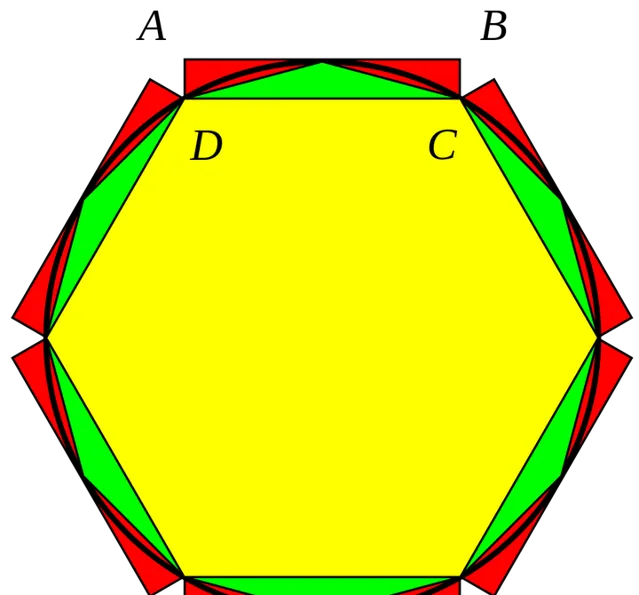
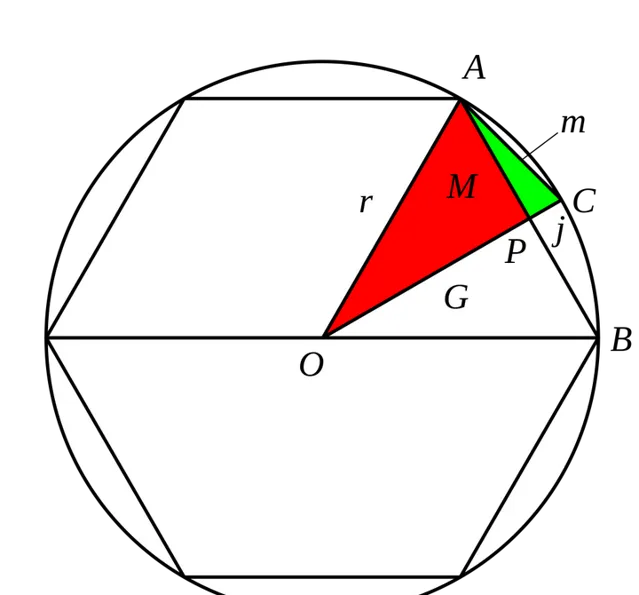
定义 A_{n} 为圆的内接正 3\cdot2^{n} 边形的面积, l_{n} 为圆的内接正 3\cdot2^{n} 边形的边长
那么由几何关系,显然有:
A_{n+1}=3\cdot 2^{n-1}\cdot r\cdot l_{n}
令圆面积为 A ,(根据几何关系)则有如下 刘徽不等式 :
A_{n+1}<A<2A_{n+1}-A_{n}
刘徽使用圆的内接正 3\cdot2^{n}
边形的面积去逼近圆面积
详见:











