原始递归函数是递归函数的一种, 理解原始递归函数需要首先真正理解什么是递归函数, 在编程语言中, 一个函数自己调用自己便称之为递归调用, 该函数也称为递归函数, 但这种说法是不严谨, 非形式化的, 要研究递归函数需要给出递归函数的精确定义。讨论函数, 首先要确定函数的定义域, 对于递归函数来说, 它的定义域为自然数集 N , 递归函数是由 3 个基本函数派生出来的, 这 3 个基本函数分别为:
- 一元零函数 z , z 的表达式为 z(n) = 0 , 即无论自变量是多少, 函数值均为 0
- 一元后继函数 s , s 的表达式为 s(n) = n+1
- k 元投影函数 p_{i}^{k} (n_{1}, ... , n_{k})= n_{i}, i = 1, ... k , 投影函数是多元函数, 允许含有任意有限个自变量, 投影函数便是以其中某一个自变量的值作为函数值
我们定义如下三条规则:
- 复合规则 。复合规则就是函数的复合, 形式化地说, 一个 m 元函数 g 和 m 个 k 元函数 h_{1}, h_{2}, ... h_{m} 可以复合成一个 k 元函数 f , f 的表达式为: f(n_{1}, ... n_{k}) = g(h_{1}(n_{1}, ... n_{k}), ... h_{m}(n_{1}, ... n_{k}))
- 递归规则 。递归规则是由 k 元函数 g 和 k+2 元函数 h 生成的 k+1 元函数 f , f 的生成方式为:
f(n_{1}, ... n_{k}, 0) = g(n_{1}, ... , n_{k})
f(n_{1}, ... , n_{k}, n+1) = h(n_{1}, ... , n_{k}, n, f(n_{1}, ... , n_{k}, n))
这是一个一般化的写法, 取 k=0 , g 便是一个 0 元函数, 0 元函数实际上就是一个常数, 我们将该常数用 c 表示, 此时便得到了该规则最简单的形式, 即
f(0) = c
f(n+1) = h(n, f(n))
即使用常数 c (0 元函数)和二元函数 h 生成了一元递归函数 f
3. \mu 算子规则 。 \mu 算子又称最小数算子, 它的定义是: 我们设 k+1 元函数 g 对于任意自然数 n_{1}, ... , n_{k} 都存在自然数 x 使得 g(n_{1}, ... , n_{k}, x) = 0 , 换句话说, 方程 g=0 在自然数集上总有根, 则我们可以定义 k 元函数 f , f 的表达式为 f=(n_{1}, ... , n_{k}) = min\{x| g(n_{1}, ... , n_{k}, x) = 0\} , 即 f 的函数值便是使方程 g=0 成立的最小自然数根, 此时我们称函数 f 是由函数 g 使用 \mu 算子生成的
有了如上的定义, 现在我们可以给出递归函数的一般定义:
由一元零函数, 一元后继函数, k 元投影函数这三个基本函数, 经过有限次地使用复合规则, 递归规则, \mu 算子规则得到的函数是递归函数.
这是递归函数最一般, 最抽象的定义。而 原始递归函数则是移除了 \mu 算子规则, 即由 3 个基本函数通过有限次地使用复合规则以及递归规则得到的函数便称为原始递归函数 , 原始递归函数隶属于递归函数, 是递归函数的一种。
有了如上的定义我们可以分别给出原始递归函数的一些例子, 我们设 f(0) = 0 , f(n+1) = n + f(n) , 则函数 f 是一个原始递归函数, 它是由基本函数(一元零函数)使用规则 2 (递归规则) 派生出的; 再例如算术中的加法, 乘法都是原始递归函数, 以加法为例, 加法的本质是一个二元函数 y = f(n_{1}, n_{2}) , 其中 n_{1}, n_{2} 分别是加数和被加数, 加法函数可以由如下两个式子使用规则 2 (递归规则) 派生出来
n_{1} + 0 = p_{1}^{1}(n_1)
n_{1} + (n+1) = (n_{1} + n) + 1 = s(p_{3}^{3}(n_{1}, n, n_{1} + n))
其中 1 式是一元投影函数, 右侧函数只有一个自变量, 它的函数值恒等于自变量本身的值 (即该函数是 3 个基本函数之一), 2 式右侧是由一个三元投影函数和一个一元后继函数使用复合规则而成的, 1 式和 2 式使用规则 2 (递归规则) 便可以生成递归函数 (即加法函数是一个二元原始递归函数), 事实上原始递归函数是非常普遍的, 加减乘除等算术运算本质上都是原始递归函数, 都可以通过 3 个基本函数使用规则 1 (复合规则) 和规则 2 (递归规则) 派生出来, 不仅如此, 符号函数 (当 n > 0 时, f(n) = 1 , 当 n=0 时 f(n) = 0 ), min 函数, max 函数, 逻辑与, 逻辑或等等都是原始递归函数
原始递归这个概念不仅仅用于函数, 也可以用于关系 (即谓词), 举例来说, 小于等于 \leq 这个关系是一种谓词, 我们可以定义关于该谓词的二元特征函数 f , f 的表达式如下:
f(x, y) = 1 , 当 x\leq y
f(x, y) = 0 , 当 x > y
若谓词的特征函数是原始递归的, 则我们称该谓词也是原始递归的, 实际上等于, 小于, 大于, 小于等于, 大于等于等等关系都是原始递归的, 事实上, 常见的绝大多数算法都可以通过原始递归函数推导出来, 在可计算性理论中可以证明, 一切原始递归函数都是可计算函数, 换句话说, 原始递归函数都可以使图灵机停机
除了原始递归函数, 还有一类递归函数, 它们无法通过如上定义的 3 个基本函数使用规则 1, 2 派生出来, 这样的函数也不难构造, 例如我们可以令 f_{1}, f_{2}, ... 表示原始递归函数的序列, 我们定义一个新的函数 F: N\rightarrow N , 它的表达式为 F(n) = f_{n}(n) + c , 其中 c 为非零常数, 函数 F 不出现在原始递归函数序列中, 所以它是一个非原始递归函数, 典型的非原始递归函数是阿克曼函数, 它的表达式如下所示:
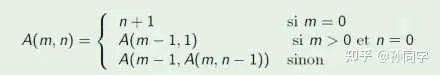参考【Computability: an introduction to recursive function theory】
