Batch Normalization

實作有多簡單,標準化+反標準化。
理論有多復雜,到目前為止,都沒有很好的理論證明,絕大多數文章還停留在實驗階段。
據我所知,BN的解釋經歷了這麽幾個主要階段:
- 避免Internal Covariate Shift
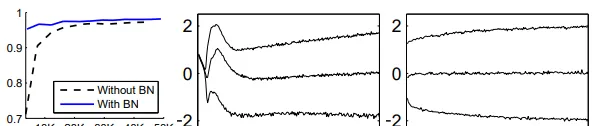
原始的BN論文給出的解釋是BN可以解決神經網路訓練過程中的ICS(Internal Covariate Shift)問題,所謂ICS問題,指的是由於深度網路由很多隱層構成,在訓練過程中由於底層網路參數不斷變化,導致上層隱層神經元啟用值的分布逐漸發生很大的變化和偏移,而這非常不利於有效穩定地訓練神經網路。
2. 平滑loss landscape
BN效果好是因為BN的存在會引入mini-batch內其他樣本的資訊,就會導致預測一個獨立樣本時,其他樣本資訊相當於正則項,使得loss曲面變得更加平滑,更容易找到最優解。相當於一次獨立樣本預測可以看多個樣本,學到的特征泛化性更強,更加general。
這個結論在之前的How Does Batch Normalization Help Optimization?文章中明確提出來過。
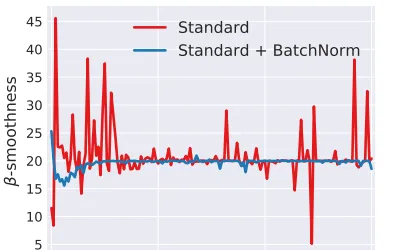
圖中展示了用L-Lipschitz函式來衡量采用和不采用BN進行神經網路訓練時兩者的區別,可以看出未采用BN的訓練過程中,L值波動振幅很大,而采用了BN後的訓練過程L值相對比較穩定且值也比較小,尤其是在訓練的初期,這個差別更明顯。這證明了BN透過參數重整確實起到了平滑損失曲面及梯度的作用。
3. 導致Information Leakage
在最近很火的對比學習中,如果在mini-batch內計算BN統計量,就會導致預測一個獨立樣本時,會引入其他mini-batch樣本的資訊,造成資訊泄露,騙過模型。
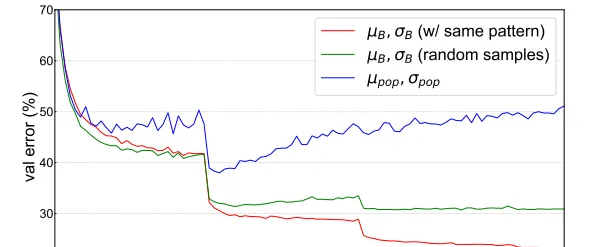
如圖所示,當使用random采樣的mini-batch統計量時,驗證誤差會增加,當使用population統計量時,驗證誤差會隨著epoch的增加逐漸增大,導致明顯的過擬合,驗證了BN資訊泄露問題的存在。
即便是在理論如此匱乏的情況下,BN也孕育出了許許多多的變體,比如GN、LN、IN等等。
batch normalization可以說是深度學習時代的black art,或者說是necessary evil。
Reference
[1] Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
[2] How Does Batch Normalization Help Optimization?
[3] Rethinking "Batch" in BatchNorm











