原始遞迴函式是遞迴函式的一種, 理解原始遞迴函式需要首先真正理解什麽是遞迴函式, 在程式語言中, 一個函式自己呼叫自己便稱之為遞迴呼叫, 該函式也稱為遞迴函式, 但這種說法是不嚴謹, 非形式化的, 要研究遞迴函式需要給出遞迴函式的精確定義。討論函式, 首先要確定函式的定義域, 對於遞迴函式來說, 它的定義域為自然數集 N , 遞迴函式是由 3 個基本函式衍生出來的, 這 3 個基本函式分別為:
- 一元零函式 z , z 的運算式為 z(n) = 0 , 即無論自變量是多少, 函式值均為 0
- 一元後繼函式 s , s 的運算式為 s(n) = n+1
- k 元投影函式 p_{i}^{k} (n_{1}, ... , n_{k})= n_{i}, i = 1, ... k , 投影函式是多元函式, 允許含有任意有限個自變量, 投影函式便是以其中某一個自變量的值作為函式值
我們定義如下三條規則:
- 復合規則 。復合規則就是函式的復合, 形式化地說, 一個 m 元函式 g 和 m 個 k 元函式 h_{1}, h_{2}, ... h_{m} 可以復合成一個 k 元函式 f , f 的運算式為: f(n_{1}, ... n_{k}) = g(h_{1}(n_{1}, ... n_{k}), ... h_{m}(n_{1}, ... n_{k}))
- 遞迴規則 。遞迴規則是由 k 元函式 g 和 k+2 元函式 h 生成的 k+1 元函式 f , f 的生成方式為:
f(n_{1}, ... n_{k}, 0) = g(n_{1}, ... , n_{k})
f(n_{1}, ... , n_{k}, n+1) = h(n_{1}, ... , n_{k}, n, f(n_{1}, ... , n_{k}, n))
這是一個一般化的寫法, 取 k=0 , g 便是一個 0 元函式, 0 元函式實際上就是一個常數, 我們將該常數用 c 表示, 此時便得到了該規則最簡單的形式, 即
f(0) = c
f(n+1) = h(n, f(n))
即使用常數 c (0 元函式)和二元函式 h 生成了一元遞迴函式 f
3. \mu 算子規則 。 \mu 算子又稱最小數算子, 它的定義是: 我們設 k+1 元函式 g 對於任意自然數 n_{1}, ... , n_{k} 都存在自然數 x 使得 g(n_{1}, ... , n_{k}, x) = 0 , 換句話說, 方程式 g=0 在自然數集上總有根, 則我們可以定義 k 元函式 f , f 的運算式為 f=(n_{1}, ... , n_{k}) = min\{x| g(n_{1}, ... , n_{k}, x) = 0\} , 即 f 的函式值便是使方程式 g=0 成立的最小自然數根, 此時我們稱函式 f 是由函式 g 使用 \mu 算子生成的
有了如上的定義, 現在我們可以給出遞迴函式的一般定義:
由一元零函式, 一元後繼函式, k 元投影函式這三個基本函式, 經過有限次地使用復合規則, 遞迴規則, \mu 算子規則得到的函式是遞迴函式.
這是遞迴函式最一般, 最抽象的定義。而 原始遞迴函式則是移除了 \mu 算子規則, 即由 3 個基本函式透過有限次地使用復合規則以及遞迴規則得到的函式便稱為原始遞迴函式 , 原始遞迴函式隸屬於遞迴函式, 是遞迴函式的一種。
有了如上的定義我們可以分別給出原始遞迴函式的一些例子, 我們設 f(0) = 0 , f(n+1) = n + f(n) , 則函式 f 是一個原始遞迴函式, 它是由基本函式(一元零函式)使用規則 2 (遞迴規則) 衍生出的; 再例如算術中的加法, 乘法都是原始遞迴函式, 以加法為例, 加法的本質是一個二元函式 y = f(n_{1}, n_{2}) , 其中 n_{1}, n_{2} 分別是加數和被加數, 加法函式可以由如下兩個式子使用規則 2 (遞迴規則) 衍生出來
n_{1} + 0 = p_{1}^{1}(n_1)
n_{1} + (n+1) = (n_{1} + n) + 1 = s(p_{3}^{3}(n_{1}, n, n_{1} + n))
其中 1 式是一元投影函式, 右側函式只有一個自變量, 它的函式值恒等於自變量本身的值 (即該函式是 3 個基本函式之一), 2 式右側是由一個三元投影函式和一個一元後繼函式使用復合規則而成的, 1 式和 2 式使用規則 2 (遞迴規則) 便可以生成遞迴函式 (即加法函式是一個二元原始遞迴函式), 事實上原始遞迴函式是非常普遍的, 加減乘除等算術運算本質上都是原始遞迴函式, 都可以透過 3 個基本函式使用規則 1 (復合規則) 和規則 2 (遞迴規則) 衍生出來, 不僅如此, 符號函式 (當 n > 0 時, f(n) = 1 , 當 n=0 時 f(n) = 0 ), min 函式, max 函式, 邏輯與, 邏輯或等等都是原始遞迴函式
原始遞迴這個概念不僅僅用於函式, 也可以用於關系 (即謂詞), 舉例來說, 小於等於 \leq 這個關系是一種謂詞, 我們可以定義關於該謂詞的二元特征函式 f , f 的運算式如下:
f(x, y) = 1 , 當 x\leq y
f(x, y) = 0 , 當 x > y
若謂詞的特征函式是原始遞迴的, 則我們稱該謂詞也是原始遞迴的, 實際上等於, 小於, 大於, 小於等於, 大於等於等等關系都是原始遞迴的, 事實上, 常見的絕大多數演算法都可以透過原始遞迴函式推匯出來, 在可計算性理論中可以證明, 一切原始遞迴函式都是可計算函式, 換句話說, 原始遞迴函式都可以使圖靈機停機
除了原始遞迴函式, 還有一類遞迴函式, 它們無法透過如上定義的 3 個基本函式使用規則 1, 2 衍生出來, 這樣的函式也不難構造, 例如我們可以令 f_{1}, f_{2}, ... 表示原始遞迴函式的序列, 我們定義一個新的函式 F: N\rightarrow N , 它的運算式為 F(n) = f_{n}(n) + c , 其中 c 為非零常數, 函式 F 不出現在原始遞迴函式序列中, 所以它是一個非原始遞迴函式, 典型的非原始遞迴函式是阿克曼函式, 它的運算式如下所示:
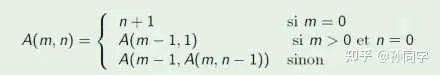 參考【Computability: an introduction to recursive function theory】
參考【Computability: an introduction to recursive function theory】










