計算陳數和貝裏曲率是凝聚態拓撲中繞不開的問題(有 non-trivial winding number?),該技術活有很多細節,導致包括我自己在內的許多初學者望而卻步。問導師他也是甩給我05年那篇「日本人寫的JPS」(https:// doi.org/10.1143/JPSJ.74 .1674 ),叫我自己把玩,奈何領悟能力實在太差,遂而棄之食土,再加上日常虛度時光,每每想起只無能狂暴爾。時過境遷,最近在看了關濟寰老師的BLOG後忽覺摸到了陳數計算的門檻,遂寫下這篇小筆記療以自慰。
對於一個二維周期性晶格,布里元區是一Torus,其第n條帶的陳數可以看作廣義的「磁通量」:
\begin{align} C_{n}=\frac{1}{2\pi i}\int_{T^{2}} d^{2}k \space F(k) \tag{1} \end{align}\\
其中 \begin{align} F \end{align} 叫做Berry curvature,貝裏曲率,可簡單地當作「磁場」來理解,從而可以定義一個「向量勢」 A_{\mu}\left(k\right),(\mu=1,2) ,滿足 \begin{align} F\left(k\right)=\nabla \times \vec{A}=\partial_{1}A_{2}\left(k\right)-\partial_{2}A_{1}\left(k\right) \end{align} 。根據量子力學,該「失勢」正是Berry connection:
\begin{align} A_{\mu}=\langle n\left(k\right) | \partial_{\mu} | n(k) \rangle \tag{2} \end{align}\\
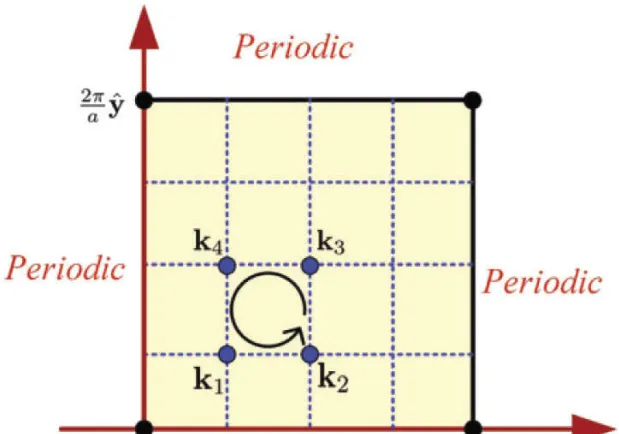
\begin{align} |n(k)\rangle \end{align} 是第n條帶的Bloch哈密頓本征方程式的本征矢,滿足 \begin{align} H(k)| n(k)\rangle = E_{n}(k) | n(k) \rangle \tag{3} \end{align}\\ 因此在給定Bloch哈密頓 \begin{align} H_{k} \end{align} 後,若想計算某條帶的陳數,一個直白的思路是:先將布里元區離散化取點,用for迴圈對每個倒空間格點求解一組本征方程式(3),將求得的波函式做兩個方向的數值差分(數值求導)後再與自身作內積,即(2);Berry curvaure也是透過對(2)的有限差分得到,由於Berry curvature涉及到 A_{\mu} 在 \nu 方向的偏移( \mu \neq \nu ),所以需要涉及到 (k_{x},k_{y}) 附近的四個點。(1)最終求得陳數的過程就是將積分變為求和。由於積分區域遍及個布里元區,所以要對每次迴圈的 (k_{x},k_{y}) 作累加。
但是這樣的操作會遇到所謂的規範問題或者隨機相位問題,什麽意思呢?就是在對固有函數做數值求導時,我們需要兩個本征波函式 \begin{align} f(k) \end{align} 和 \begin{align} f(k+\delta k) \end{align} 做減法,也就是說要求解兩次本征方程式,那麽問題是,雖然兩次求解的固有函數雖然模方十分接近,都是本征解,但matlab在兩次呼叫eig函式時選的規範不同,從而做減法(差分)時就會出現巨大差別,導致結果不收斂。用公式表達就是這個意思:
\begin{align} | n(k) \rangle \rightarrow e^{-i \lambda (k)} | n(k) \rangle, \space A_{\mu}(k) \rightarrow A_{\mu}(k)-i \partial_{\mu} \lambda (k) \tag{4} \end{align}\\
為了解決這一問題需要加入尋找波函式統一規範的步驟,具體內容可見關濟寰老師的Blog:陳數Chern number的計算(定義法)(附Python、Matlab程式碼) - Ji-Huan Guan (guanjihuan.com)
這裏直奔主題,采用「日式高效法」,利用采取U(1) link的方案來避免隨機相位的幹擾,也就是原文的精華部份:

品質項石墨烯的Berry curvature偽碼:
%四個點的波函式
V
=
getvec
(
HG
(
kx
(
ii
)
,
ky
(
jj
)));
Vkx
=
getvec
(
HG
(
kx
(
ii
)
+
delta
,
ky











