深入淺出GPU最佳化系列：GEMM最佳化（一）

本篇文章是深入淺出GPU最佳化系列的第兩個專題，主要是 介紹如何對GPU中的矩陣乘法（GEMM）進行最佳化 。目前針對GEMM的最佳化，網路上已經有非常多的教程和範例了。大部份的重要資料我都看了看。但總的來說，還是不夠接地氣，然後理解起來還是會比較費解。所以希望寫這麽一篇文章，盡可能地去把GPU的GEMM最佳化說清楚，說明白。然後讓小白讀者也能透過這麽一兩篇文章去更好地了解GEMM最佳化的相關技術。

不像上次的reduce最佳化一樣，能一篇文章說完。這次的GEMM最佳化會分為三個部份。 第一個部份只說最佳化思路和分析 ，沒有任何程式碼，這麽做考慮也是為了減輕讀者的負擔，看程式碼太累， 盡可能地讓讀者先明白原理，為什麽要這麽做 。 第二個部份是對程式碼的詳細解析，這個裏面就是一行一行地去分析程式碼 。因為之前的很多部落格進行了分析，但是程式碼本身並沒有開源，或者說開源了程式碼，但沒有解析，看起來太累了。我希望提供一個盡可能詳細的程式碼解析，讀者看完之後能明白相關最佳化技巧，並且可以直接把程式碼拿去驗證使用。 第三個部份主要涉及到組譯器 ，最重要的是說明在NV的卡上，怎麽去解決寄存器的bank沖突來獲取極致的效能。

本篇文章是 GEMM最佳化的第一個部份 ，在這篇文章中，只說 最佳化思路和分析 。

前言

在高效能領域，對於 矩陣乘（GEMM）的最佳化 是一個非常重要的課題。GEMM可以非常廣泛地套用於航空航天、流體力學等科學計算領域，這也是之前HPC的主要套用場景。後來深度學習開展地如火如荼，由於對高算力的需要，也成為HPC的主要套用場景之一。這些年湧現了一系列的深度學習模型。模型裏面最耗時的東西，包括摺積、全連線層、attention，都可以轉換成GEMM操作。所以說，GEMM最佳化的重要性，怎麽突出都不過分。

目前網上能找到的針對GEMM最佳化的資料主要有這麽幾個方面：
一、論文 ，目前針對GPU進行GEMM最佳化的論文非常多，這裏主要推薦Understanding the GPU Microarchitecture和Fast implementation of dgemm on fermi gpu以及 Dissecting the NVIDIA Volta GPU Architecture via Microbenchmarking。這幾篇論文在業界都比較有影響力，就是程式碼開源方面做的不算太好。 二、官方部落格 ，主要是CUTLASS和NervanaSystems-SGEMM最佳化。還有前段時間曠視發的文章CUDA矩陣乘法最佳化，寫的都很詳細。 三、github 的一些demo，程式碼量不大，看起來比較舒服。我是看了這兩個，

demo1程式碼寫的好理解一些，但是最佳化工作沒做完全，沒有做到prefetch。demo2是效果很好，11個最佳化技巧，不斷逼近cublas。但是程式碼真的看起來比較難受，最重要的很多參數寫死了，不好去調。

總而言之，目前列舉的上述資料存在著這麽兩個問題：一、文件方面，讀起來還是比較費勁，對於小白來說，還是不夠簡單不夠傻，看起來太累了；二、程式碼方面，要麽是沒公開程式碼，要麽是程式碼太多了，看不下去；還有的就是程式碼可讀性很強，但是最佳化工作還不是特別深，或者就是程式碼最佳化做的很好，但是可讀性差了。方方面面總是有點欠缺，所以希望能夠寫一篇盡可能地在文件上簡單明了，在程式碼上詳細且可讀性好的文章。當然，這是一個逐步叠代的過程，所以這篇文章也會持續進行更新哈。

本篇文章主要是采納了cutlass的行文思路，主要介紹GEMM中的數據分塊和如何在多級儲存進行數據搬運。這也是 HPC最佳化的核心思想，怎麽樣讓數據放在更近的儲存上來掩蓋計算的延時，從而減少儲存墻的影響 。文章分為四個方面進行敘述，首先介紹在global memory層面如何進行分塊以及數據搬運，隨後介紹在shared memory層面如何進行分塊以及數據搬運，而後介紹在register層面如何進行分塊以及避免bank沖突，最後介紹如何進行prefetch以更好地掩蓋訪存時延。

從global memory到shared memory

假設有矩陣A,B，需要計算矩陣A和B的乘，即矩陣C。A、B、C三個矩陣的維度分別為m*k，k*n，m*n\ ，且三個矩陣中的數據都是單精度浮點數。對於C中每一個元素，C[i][j]，可以看作是A的一行和B的一列進行一次歸約操作。采用最naive的GEMM演算法，在GPU中，一共開啟m*n\ 個執行緒，每個執行緒需要讀取矩陣A的一行與矩陣B的一列，而後將計算結果寫回至矩陣C中。因而，完成計算一共需要從global memory中進行 2mnk\ 次讀操作和m*n次寫操作。大量的訪存操作使得GEMM效率難以提高，因而考慮global memory中進行分塊，並將矩陣塊放置到shared memory中。其示意圖如下：

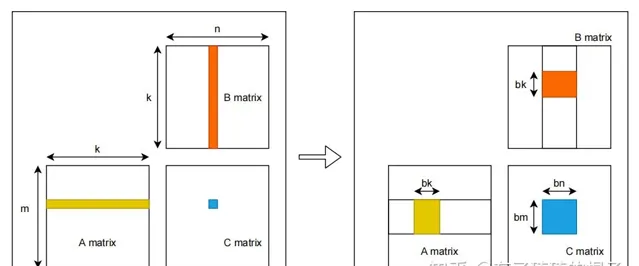
對global memory進行分塊的GEMM演算法示意圖見上圖右側。首先將A、B、C三個矩陣劃分為多個維度為bm*bk，bk*bn，bm*bn\ 的小矩陣塊。三個矩陣形成M*K，K*N，M*N\ 的小矩陣網格。其中，M=m/bm，N=n/bn，K=k/bk\ 。隨後在GPU中開啟M*N\ 個block，每個block負責C中一個維度為bm*bn\ 的小矩陣塊的計算。計算中一共有K次叠代，每一次叠代都需要讀取A中一個維度為bm*bk\ 的小矩陣塊和B中一個維度為bk*bn\ 的小矩陣塊，並將其放置在shared memory中。因而，完成C中所有元素的計算一共需要從global memory中讀取M*N*K*（bm*bk+bk*bn）\ ，即m*n*k（1/bm+1/bn）\ 個單精度浮點數。相比於naive的GEMM演算法，訪存量減少為原來的 1/2*(1/bm+1/bn)\ 。透過global memory中分塊演算法極大地減少了對global memory的訪存量。並且，相比於naive演算法，對global進行分塊可以更充分地利用數據局部性。在naive演算法中，每一個執行緒都需要直接從global memory中取數，其時延非常長，計算效能非常差。而進行分塊後，將維度為bm*bk，bk*bn\ 的小矩陣塊先儲存到shared memory之中。而後計算單元進行計算時可以直接從shared memory中取數，大大減少了訪存所需要的時延。

從shared memory到register

隨後，我們進一步考慮從shared memory到register的過程。在這裏，只分析 一個block 中的計算。當進行K輪叠代中某一輪叠代時，GPU將維度為bm*bk，bk*bn\ 的小矩陣塊儲存到shared memory中，而後各個執行緒將shared memory中的數據存入register中進行計算。

在 不對shared memory分塊 時，一個block中含有bm*bn\ 個執行緒， 每一個執行緒負責C中一個元素的計算 。則一個block一共需要對shared memory進行 2*bm*bn*bk\ 次讀操作。而後 考慮對shared memory進行分塊 ，對bm*bn\ 的小矩陣進行再一次劃分，將其劃分為多個維度為rm*rn\ 的子矩陣。則一個block需要負責X*Y\ 個子矩陣。其中，X=\frac{bm}{rm}\ ，Y=\frac{bn}{rn}\ 。隨後，在一個block中開啟X*Y\ 個執行緒， 每個執行緒負責一個維度為rm*rn\ 的子矩陣的計算 。在計算中，一個block一共需要從shared memory讀取X*Y*(rm+rn)*bk\ ，即bm*bn*bk*(\frac{1}{rm}+\frac{1}{rn})\ 個單精度浮點數。相比於未分塊的演算法，對於shared memory中的訪存量減少為原來的 1/2*(\frac{1}{rm}+\frac{1}{rn})\ 。並且，由於將數據放入register中，可以直接對數據進行運算，減少了從shared memory中取數的時延。

register分塊

在這裏，我們考慮最後一層，即register中的計算，並且只分析一個thread。在完成以上的過程後，對於一個執行緒而言，它現在擁有：rm\ 個A矩陣的寄存器值，rn\ 個B矩陣的寄存器值，以及rm *rn\ 個C矩陣的寄存器值。透過這些寄存器的值，需要計算rm*rn\ 個數。這需要rm *rn\ 條FFMA指令。

這個時候會涉及到寄存器的bank conflict。在NV的GPU中，每個SM不僅會產生shared memroy之間的bank 沖突，也會產生寄存器之間的bank沖突。這一點對於計算密集型的算子十分重要。像shared memory一樣，寄存器的Register File也會被分為幾個bank，如果一條指令的的源寄存器有2個以上來自同一bank，就會產生沖突。指令會重發射，浪費一個cycle。PS：這個地方是從曠視的部落格中看的。然後對於maxwell架構的GPU而言，bank數為4，寄存器 id%4 即所屬bank。

我們假設對這個thread來說，rm=4,rn=4\ 。並且計算C的寄存器以一種非常naive的情況分配，如下圖左側所示。則需要產生16條FFMA指令，列舉如下：

可以從中看出，這會產生大量的register bank沖突，所以需要對參與計算的寄存器重新進行分配和排布,如上圖右側所示。在有些地方，這種方式也可以叫做register分塊。

數據的prefetch

最後，我們來講講如何透過對數據進行prefetch來減少訪存的latency。我們再來回顧GEMM的過程，並且仔細地看看這個訪存的latency到底是怎麽導致的。 對於一個block而言 ，需要計算一個bm*bn\ 的矩陣塊，這個時候需要進行K次叠代，每次叠代都需要先將來自A和B的兩個小塊送到shared memory中再進行計算。而從global中訪存實際上是非常慢的，所以導致了latency。雖然GPU中可以透過block的切換來掩蓋這種latency，但是由於分配的shared memory比較多，活躍的block並不太多，這種延時很難被掩蓋。 對於一個thread ，需要計算一個rm*rn\ 的小矩陣，但是必須先將數據從shared memory傳到寄存器上，才能開始進行計算。所以導致了每進行一次叠代，計算單元就需要停下來等待，計算單元不能被餵飽。

為此，需要進行數據的Prefetch來盡可能地掩蓋這種latency。思想也比較簡單，需要多開一個buffer，進行讀寫分離。示意圖如下。當block進行第2輪叠代時，需要對A2和B2進行計算，在計算單元進行計算的同時，我們將A3和B3提前放置到shared memory。而後，在進行第3輪叠代時，就可以直接對shared memory中的A3和B3進行計算，而不需要等待從global memory搬運到shared memory的時間。寄存器上的Prefetch也是同理。

總結

GEMM的最佳化思想，基本上就是這麽幾方面的內容。希望大家透過介紹能夠對GEMM的最佳化有一個比較直觀且具體的理解。（感覺寫的還是有點亂，圖也沒畫的太好，大家諒解）。當然，看完這些，要開始寫程式碼的時候，大家還是會比較懵，也不知道這些東西應該怎麽實作。現在寫了詳細的解析，也就是GEMM最佳化（二）。去實作了上述最佳化技巧和細致地分析每一行程式碼，大家可以看一看。

第三部份中，更細粒度的CUDA C程式碼調優和關於組譯程式碼的調優，也已經給出。

最後， 感謝大家看到這裏，有什麽問題歡迎跟我討論哈 。關於GPU的最佳化，打算寫一個系列，說說GPU最佳化的一些經典問題和最佳化技巧。不過最近工作也比較忙，更新估計很慢。之前已經寫完了

的內容。希望後面能堅持下去。

歡迎大家關註哈:)