幾何的觀點 :如果把方陣視為線性變換,則其行列式的絕對值表示該線性變換造成的體積元的變化系數,行列式的符號反映了基底的定向變化。
比如,行列式可表示平行四邊形或平行六面體的有向面積/體積,因為平行四邊形和平行六面體實際上分別是平面和空間中另一組基底構成的面積元/體積元。
比如,行列式為零,表示線性變換是奇異的,即把原空間的體積元變成零了,一一對應就不存在了
又比如,導數實際上是線性變換 (微分實際上是兩個切空間之間的線性變換,比如一元函式實際上是一維實數軸到一維切線之間的線性變換,得到的斜率只是一個數,但實際上是1x1矩陣),於是積分變換中的Jacob行列式實際上是此線性變換的行列式,它的絕對值是體積元dxdydz的系數。
代數的觀點 : 行列式無非是方陣的一個函式,但它是一種反對稱多重線性型,比如f(\alpha x_1,x_2,x_3)=\alpha f(x_1,x_2,x_3) ,-f(x_1,x_2,x_3)=f(x_2,x_1,x_3) ,多重線性性體現在每一行或每一列的線性性質,反對稱體現在兩行或兩列交換後變負。同為行和列的反對稱多重線性型,行列式的計算方式也就確定了。
這兩種觀點都不允許非方陣的行列式的定義。
===============================================================
補充一下,問一個數學工具的本質,竊以為並不妥當,有一點追求終極真理的感覺,在哲學上並不能自洽。不如先看一下它的歷史,然後再觀察一下它有哪些深刻的套用。
歷史上,行列式先於矩陣,用於求解線性方程式。行列式是否為零可用來判定一個線性方程式是否有解,然後Cramer規則直接用行列式給出線性方程式的解。隨後,行列式才被視為一個矩陣的函式。
數學上的兩條重要的主線:解方程式和微積分線上性代數上統一起來了,因為微分實際上就是一種線性逼近。因而,矩陣和行列式在這其中起到的作用就非常深刻了。而行列式作為一個函式具有的反對稱線性性在抽象代數是一個非常重要的概念。
所以說,行列式只不過是數學家在解決實際問題時發明的一個很好用的工具,恰好它又可以在許多的套用中發揮作用。
================================================================
再補充一下,幾個常用的行列式套用
-
積分變換與Jacob行列式 (體積元都為正,所以取行列式的絕對值)
(v_1,\cdots,v_n)=\varphi(u_1,\cdots,u_n) \Rightarrow dv_1 \cdots dv_n = |\det(\operatorname{D}\varphi)(u_1, \ldots, u_n)| \, du_1 \cdots du_n
-
Cramer規則
Ax=b 的解為x_i=\frac{|A_i|}{|A|} ,其中A_i 為將A 的第i 列換成b
-
平行四邊形面積,從原點出發的兩個向量\boldsymbol{v}_1,\boldsymbol{v}_2
構成的平行四邊形的有向面積為
\operatorname{det}(\boldsymbol{v}_1,\boldsymbol{v}_2)=\left|\begin{matrix}v_{11},v_{21}\\v_{12},v_{22}\end{matrix}\right|
-
平行六面體體積

-
叉乘的另一種定義
(x_1,y_1,z_1)^T\times(x_2,y_2,z_2)^T=\left|\begin{matrix}i&j&k\\x_1&y_1&z_1\\x_2&y_2&z_2\end{matrix}\right|
-
判斷共面
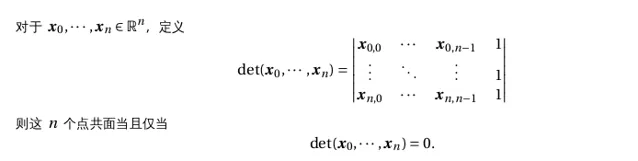
-
判斷共圓












