袁講經典13：一道碰撞問題的三種解法，看一看哪一種最妙！
例： 如圖所示，不記重力，空間有勻強電場 E 。有兩個品質均為 m 的小球，A帶電 q>0 ，B無電荷。 t=0 時，兩球靜止，且相距 L ，AB方向與 E 方向相同。 t=0 時刻，A開始受電場力而運動。A、B間發生彈性正碰，且無電量轉移，求第8次正碰到第9次正碰之間需要的時間。
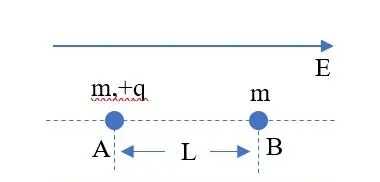
解1： 慢慢嘗試計算，尋找規律，
首先，計算A在電場中運動的加速度，為， a=\frac{Eq}{m} ，
根據位移公式，計算A和B首次碰撞時間， L=\frac{1}{2}at_1^2 ，
解得， t_1=\sqrt\frac{2mL}{Eq} ，
此時， v_{A1}=at_1=\sqrt\frac{2EqL}{m} 。
然後發生第一次彈性碰撞，這裏省略計算過程，直接根據「等質換速」得到碰撞後的速度為，
v_{A1}'=0 ，然後A做加速度為 a 的勻加速運動，
v_{B1}’=v_{A1}=\sqrt\frac{2EqL}{m} ，然後B作勻速直線運動，
再然後計算從第一次碰撞到第二次碰撞的時間，也就是再次相遇時間，得到，
\frac{1}{2}at_2^2=v_{B1}’t_2 ，
解得， t_2=2\sqrt{\frac{2mL}{Eq}} ，
再再然後計算，第二次碰撞前A和B的速度大小，
v_{A2}=at_2=2\sqrt\frac{2EqL}{m} ， v_{B2}=v_{B1}’=\sqrt\frac{2EqL}{m}
碰撞後交換速度，得到，
v_{A2}’=v_{B2}=\sqrt\frac{2EqL}{m} ，然後作勻加速運動，
v_{B2}'=v_{A2}=2\sqrt\frac{2EqL}{m} ，然後作勻速直線運動，
計算相遇時間為， v_{A2}’t_3+\frac{1}{2}at_3^2=v_{B2}’t_3 ，
解得， t_3=2\sqrt{\frac{2mL}{Eq}} ，
此時，我們發現了， t_3=t_2=2\sqrt{\frac{2mL}{Eq}} ，
再次嘗試下一輪碰撞，發現， t_4=t_3=t_2=2\sqrt{\frac{2mL}{Eq}} ，
所以，最終得到，第8次正碰到第9次正碰之間需要的時間也為 2\sqrt{\frac{2mL}{Eq}} 。
上述方法，原理上很簡單，但是計算很煩躁，易亂，且不理解為啥兩次碰撞的相鄰時間間隔都是相同的，有一種弄通了一半的感覺。
解2： 變換參考系的方法，
由解法1可知，
第一次碰撞前， v_{A1}=\sqrt\frac{2EqL}{m} ， v_{B1}=0 ，
第一次碰撞後， v_{A1}’=0 ，v_{B1}’=\sqrt\frac{2EqL}{m} ,
然後， 我們選擇碰撞後的B為參考系 ，則，
B為靜止的，
A以 \sqrt\frac{2EqL}{m} 速度反向減速到零，再正向加速到 \sqrt\frac{2EqL}{m} ，此時經歷的時間為， t=2\sqrt\frac{2EqL}{m}/a=2\sqrt{\frac{2mL}{Eq}} 。
此時，A和B碰撞交換速度，在上述參考系中，交換速度後，
A的速度為 0 ，B的速度為 \sqrt\frac{2EqL}{m} ，
然後再次變換參考系， 選擇新一輪碰撞後的B作為參考系， 則，
B是靜止的，然後A相對B的運動同第一次碰撞後的情況，於是，
再次相遇碰撞的時間為， 2\sqrt{\frac{2mL}{Eq}} 。
所以，最終任意兩次碰撞之間的時間間隔都為， 2\sqrt{\frac{2mL}{Eq}} 。
上述方法，計算量較小，也可以更好地從本質上理解為什麽任意兩次碰撞之間的時間間隔相等，但是呢？要從變換參考系的角度去理解呢，思維強度挺大的，費腦子。
另外，小夥伴們可能會提出來，動量守恒可以變換參考系使用嗎？特別是「等質換速」在不是地面的參考系中能否使用呢？關於這個問題，我在文章「袁野：從一道經典習題淺議參考性等價及無窮小問題（2）」介紹過了，感興趣的小夥伴，可以看一看哈！
解3： 我們可以采用影像法求解，應該是又簡單快捷又形象易理解吧。如下，註意碰撞交換速度在影像中的體現，
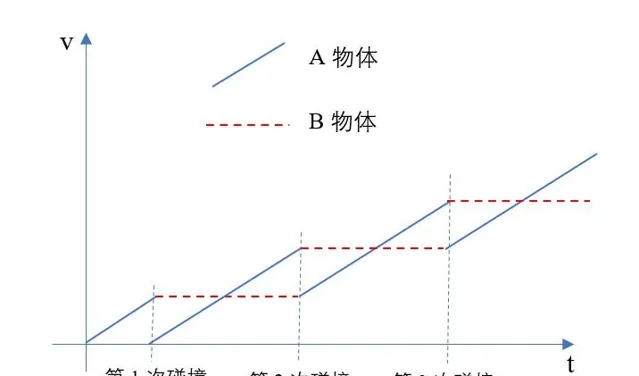
從圖中可以看出，相鄰兩次碰撞的時間間隔都是相等的，且等於A物體從開始運動到第一次碰撞的時間的2倍，即 t=2t_1=2\sqrt\frac{2mL}{Eq} 。
好了，小夥伴們應該也發現了，哪種方法最簡單了吧，影像法，直觀，形象，好理解。
小夥伴們或許會問，什麽時候用影像法呢？
其實關於運動學的問題，是我們進入高中學物理的第一階段的知識點，個人認為還是挺難的，公式也多，方法有時候很巧妙。
我一般建議，在「單物體單狀態」運動中，直接采用公式法，公式可以簡單記為，
一個概念， 加速度 a 。
二個基本公式 ，
v=v_0\pm at ， x=v_0t\pm\frac{1}{2}at^2 ，
三個連等式 ，
\bar{v}=\frac{x}{t}=\frac{v_0+v}{2}=v_{\frac{t}{2}} ,
四個匯出結論 ，
v^2-v_0^2=2ax ,
\Delta x=aT^2 ，更一般為 x_n-x_m=(n-m)aT^2 ，
相等時間間隔位移比，
相等位移間距時間比。
具體在文章「袁野：斜面問題如何做的對，做的快，做的漂亮」中，最後有一些關於這方面的介紹。
而這裏建議采用公式計算的，主要是「單物體單狀態」，所謂的「單狀態」，小夥伴們要深入理解一點點，這個「單狀態」包含了加速度不變的往返運動，比如豎直上拋運動，很多小夥伴喜歡把豎直上拋運動當做「多狀態」運動，先計算上拋過程，再計算自由落體過程，其實大可不必，我們可以把它看做一個「單狀態」，因為，我們上面的公式都是「勻變速」運動公式，換句話說，只要加速度不變，就是一個狀態，不需要分解過程的。
而當加速度變化時，就是「多狀態」了，另外還有可能存在「多物體」，對於「多物體多狀態」的情形，我們需要分物體考慮，還需要分狀態考慮，因此計算過程相對較為復雜，此時可以考慮采用其他方法，比如變換參考系，讓一個物體不動，再比如，用 v-t 影像法，顯然，上面這道題屬於「多物體多狀態」，於是考慮了影像法。
這裏，我再跟小夥伴們分享一些關於影像法的運用，比如，在文章「袁野：變換參考系在高中物理運動學解題中的妙用」中，有一道例題，原文章采用了變換參考系的方法，題目如下，
例： 在空中某處以初速度 v_0 豎直向上丟擲一個小球A，與此同時，在小球A正上方H處有一小球B自由釋放下落，問小球A和小球B在空中相遇的時間？已知重力加速度為g，不計空氣阻力，相遇時兩小球均未落地!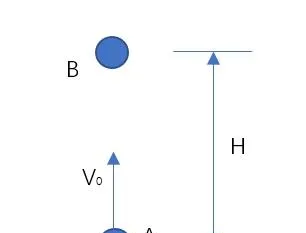
仔細想想，這題是多麽復雜呀！我們要討論以下三種情形：
1.在小球A上升過程中相遇；
2.在小球A上升後又下降過程中相遇，但未下降到丟擲點，仍在丟擲點之上；
3.在小球A下降過程中相遇，且在丟擲點之下。
這裏，我再使用影像法計算，發現根本不需要考慮上面所說的三種情形，如下，
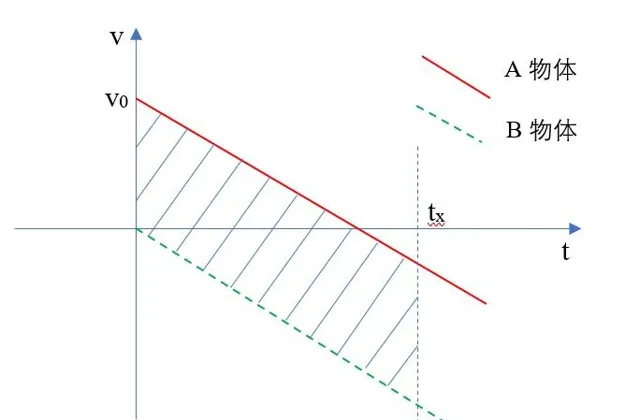
如上圖所示，無論在什麽情況下相遇，我們從圖中只要明白一件事，就是兩條速度直線所包圍面積為 H 時，即為兩小球相遇，且圖中兩條直線的斜率均為 g ，因此，所包圍面積為平行四邊形，且面積為 H 時，計算時間為， v_0t_x=H ，所以， t_x=\frac{H}{v_0} 。
多簡單，是吧！
上次還有小夥伴問這樣一道題目，大致意思是說，
例： 如下，水平傳送帶以一定速度順時針轉動，每隔時間 T 在傳送帶上靜止釋放一個物塊，物塊與傳送帶之間的動摩擦系數為 μ ，最終物塊在傳送帶上運動穩定後，物塊與物塊之間的距離為 x ，求傳送帶的速度大小？
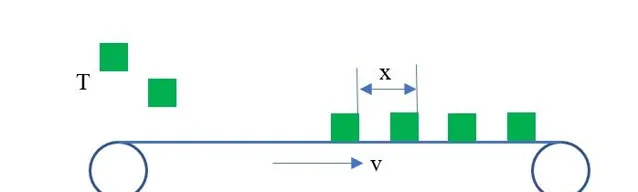
這裏，我也不多解釋了，直接畫出 v-t 影像如下，
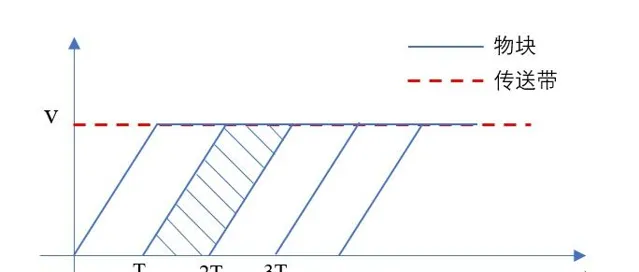
直接解得，傳送帶的速度大小為， v=\frac{x}{T} 。
好了，關於這道經典例題，就分享這麽多吧！
小夥伴們，咱們期待下次相遇經典！
