量子電腦因為采用了量子位元而帶來獨特的優勢 [1] ,但是量子計算的套用價值,坦白說直到目前為止都沒有特別明晰。與這一現狀對應的是,量子計算在輿論宣傳中被過度渲染成無所不能,而且速度快億倍以上等等,這顯然是媒體人為了文章點選率的聳人聽聞式過度發揮,並不是真實情況。
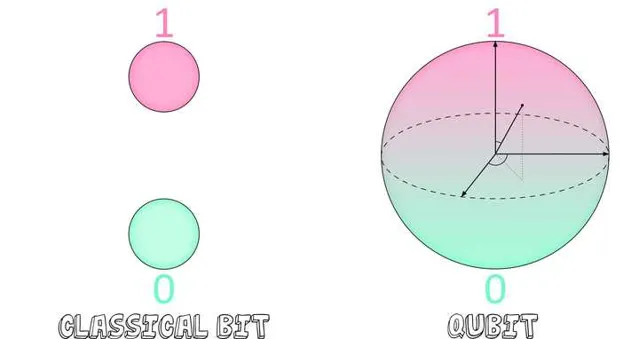
拋開量子位元的基本性質和實作這方面的復雜細節不談,量子計算的潛力完全在於量子計算演算法(Quantum algorithms) [2] . 這一特性不同於我們對普通通用電腦的理解。在通用電腦上,已經有基礎的加減乘除等基礎運算,基於這些基礎運算設計一些常見的如「摺積」、「微分」、「積分」以及更高層次的「費氏數列」、「回歸」、「分類」等演算法是比較自然而然的。但是在量子計算範疇下,這種自然而然的邏輯是不存在的,這跟量子力學奇特的性質有關。
這也就造成了量子計算不同於普通電腦通用計算的發展能力。在量子計算中,一樣需要設計每一步的步驟(比如某個數的因子分解)的基礎演算法,然後基於這些基礎演算法建設更復雜的計算套用。在類似於因子分解這樣的演算法上,量子計算擁有更好的時間復雜度 [3] . 但是在普通的加減乘除運算上,量子計算的時間復雜度更差,計算開銷顯著更差 [4] [5] . 所以,量子電腦不可能完全取代普通通用計算的電腦。要發揮量子計算的優勢,關鍵在於設計量子計算演算法。這類演算法只是用於專用計算,也就是套用場景非常特定的計算。這也就決定了,發揮量子計算優勢的量子計算演算法設計是困難的,成本高的 [2] . 而通用電腦理論上天然可以進行任意這類計算,只是在時間復雜度上有可能不可接受。
目前為止,在搜集量子計算演算法的Quantum Algorithm Zoo網站中,一共有430種專用演算法。而第一種量子計算演算法 秀爾演算法(Shor's algorithm) 的出現,已經過去了27年 [6] . 這種發展速度,對應理論上無限種的演算法數量來說,並不能讓人對量子計算的發展前景感到太樂觀。
第一種量子計算演算法秀爾演算法,把分解整數質因素的指數時間復雜度 \mathcal{O}\left( e^{1.9\left( log\: N \right)^{1/3}\left( log \: log \: N \right)^{2/3}} \right) 下降到多項式時間 \mathcal{O}\left( \left( log\:N \right)^2 \left( log\: log\: N \right)\left( log\:log\:log\:N \right) \right) . 這意味著,依賴大數因數分解困難性的RSA加密演算法 [7] ,在量子計算下變得不再安全了。因為這一問題,後量子密碼學(Post-quantum cryptography) [8] 出現,它依賴不可能被量子計算有效解決的演算法來對抗量子計算的優勢能力。目前套用廣泛的包括格密碼(Lattice-based Cryptography) [9] 等等。後量子密碼學的發展和套用,本身也說明了量子計算的局限性,它的優勢能力是可以被規避的。
從目前的情況來看,量子計算肯定不會取代我們日常使用的通用電腦,它更像是一個輔助工具,而且套用場景極為有限,套用場景的發展潛力也比較有限。目前廣泛的炒作宣傳已經透資了其潛在的價值,作為普通民眾還是應當保持冷靜,不要跟風炒作,被人在資本市場割韭菜。
參考
- ^ Holevo, A. S. (1973). Bounds for the quantity of information transmitted by a quantum communication channel. Problemy Peredachi Informatsii, 9(3), 3-11.
- ^ a b Montanaro, A. (2016). Quantum algorithms: an overview. npj Quantum Information, 2(1), 1-8.
- ^ Abbott, D. (2003). Dreams versus reality: plenary debate session on quantum computing. arXiv preprint quant-ph/0310130.
- ^ Draper, T. G. (2000). Addition on a quantum computer. arXiv preprint quant-ph/0008033.
- ^ Gidney, C. (2018). Halving the cost of quantum addition. Quantum, 2, 74.
- ^ Shor, P. W. (1999). Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM review, 41(2), 303-332.
- ^ Cocks, C. C. (1973). A note on non-secret encryption. CESG Memo.
- ^ Bernstein, D. J., & Lange, T. (2017). Post-quantum cryptography. Nature, 549(7671), 188-194.
- ^ Micciancio, D., & Regev, O. (2009). Lattice-based cryptography. In Post-quantum cryptography (pp. 147-191). Springer, Berlin, Heidelberg.










