想加的太多了，中學生自己挑一個吧：
基礎統計學
動機
理解機率和風險不僅對對沖基金經理和撲克玩家至關重要，對每個人的日常生活同樣意義重大。事實上，缺乏這種理解正是導致人類認知中一些最基本的邏輯謬誤和偏見的根源。
假設某天早上你檢視天氣預報，看到下雨機率為 50%，這究竟意味著什麽？如果你做了一個假陽性率為 2% 的癌癥檢測，你實際患癌的機率有多大？彩票、個人養老金或房貸的預期收益又是多少？
這些問題對生活中的重大決策都至關重要——從健康到選擇就讀的大學，無所不包。思考未來就意味著要思考機率，而當今的教育體系在這方面卻嚴重欠缺，未能充分培養學生這方面的能力。
牢固掌握基本的機率和統計學知識，將使學生能夠在金錢、健康和未來方面做出明智的決策，同時也能夠理解數據呈現的基本原理及其背後的含義。
合格標準
要透過本課程，學生需要參加一次現場考試，以證明他們對以下內容的理解：
頻率學派與貝葉斯學派對機率的詮釋
範例回答：
頻率學派視角：如果天氣預報說下雨機率是 10%，那麽從長期來看，我每出門 10 次，大約有 1 次會遇到雨。
貝葉斯學派視角：假設某種癌癥檢測的假陽性率是 2%，而我的檢測結果呈陽性。這並不直接意味著我患有癌癥，而是表明我患癌癥的可能性增加了 50 倍（100/2=50）。要得出在這個新資訊下我實際患癌癥的機率，我需要將這個倍數與我原本患癌癥的基礎機率相乘。
復利效應在投資和債務中的體現
範例回答：假設我借了 1,000 元，年利率是 5%。那麽一年後，我欠的金額會增加到 1,000 * 1.05 = 1,050 元；再過一年，欠款會進一步增加到 1,050 * 1.05 = 1,102.5 元，以此類推。可以看到，債務金額會以越來越快的速度增長。投資也遵循同樣的原理，只是方向是正面的，你的錢會越來越多。
平均值、中位數和眾數的區別
範例回答：平均值是所有數據的總和除以數據的個數，容易受極端值的影響。比如，在一個小公司裏，如果老板的薪資特別高，會大幅拉高整體的平均薪資。 中位數是將所有數據從小到大排列後，取中間的那個數，不易受極端值影響。在上述公司的例子中，中位數薪資能更好地反映大多數員工的真實收入水平。 眾數則是出現次數最多的數值，適合用於數據分布中有明顯重復值的情況，比如常見的鞋碼或衣服尺碼。
正態分布和冪律分布的特征
範例回答：正態分布就像人的身高分布，大多數人的身高都集中在平均水平附近，而極高或極矮的人相對較少。 冪律分布則像是名氣的分布，大多數人默默無聞，而極少數人非常出名，形成一個長尾效應。
機率中「與」、「或」和「非」的運用
範例回答：在機率計算中，每增加一個「與」條件，機率就會降低，因為這相當於在韋恩圖中取交集，滿足條件的範圍變小。「或」通常會增加機率，因為它包含了更多的可能性，但要註意不要重復計算重疊部份。（基本上是下面的圖，但不需要技術術語。）
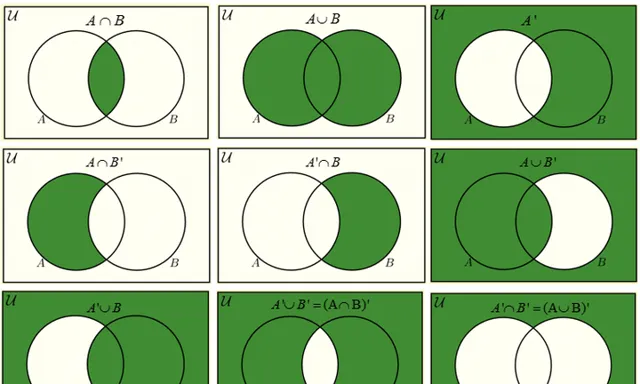期望值的計算及其套用
範例回答：期望值是將某事發生的機率與其價值相乘。例如，一張彩票售價 1 元，中獎機率是百萬分之一，獎金是 10 萬元。那麽這張彩票的期望值是 0.1 元（100,000 * 0.000001 = 0.1）。這意味著，從長期來看，你每花 1 元買彩票，平均只能得到 0.1 元的報酬，顯然不是一個好的投資。
統計和機率在實際生活中的套用
範例回答：在做人生規劃時，可以運用機率思維。比如，考慮成為社交媒體紅人這個職業選擇。雖然成功後可能收入很高，但實際上能成功的人很少，這是一個典型的冪律分布。如果我們將成功的低機率考慮進去，盡管潛在收益很高，但其期望收益可能並不如我們想象的那麽可觀。這種思考方式可以幫助我們做出更理性的決策。
基礎工業史
動機
歷史是一門教學難度極高的學科，設計相關課程更是挑戰重重。
歷史跨越數千年，涵蓋全球各地，而且每個歷史時期都可以從多角度、多維度進行解讀，這使得歷史教學的內容浩如煙海。
然而，由於我們設計的是一門必修課程——即所有學生都必須學習並透過的課程，這在一定程度上簡化了課程設計。我們可以將教學內容聚焦於我們認為每個人必須掌握的歷史知識。
在當今時代，中國學生並不需要了解羅馬帝國或古希臘的歷史。事實上，他們甚至不需要深入學習唐朝或宋朝的具體細節——因為這些知識在他們的日常生活中很少派得上用場。
相反，這些學生確實需要理解的是：現代社會與人類歷史上的其他時期有何不同，以及造成這種差異的原因。他們需要明白，他們所生活的這個富足時代是如何形成的，以及是什麽力量在支撐著我們當前的社會制度和生活方式。
如果不能理解這些關鍵問題，公民在面對稅收、監管和治理等議題時就可能做出錯誤的選擇。這種認知缺失還會導致人們對財富的創造和分配產生嚴重誤解，而這種誤解恰恰是人類歷史上一些最可怕政權得以興起的溫床。
合格標準
為了透過本課程，學生需要參加一次現場考試，以證明他們對以下內容的理解：
工業革命的核心理念，包括人均可用能源的增加、精密測量技術的套用，以及可互換零件的使用。
範例回答：盡管煤炭的使用對環境造成了負面影響，但它使人類首次能夠大規模利用非人力和畜力的能源。結合精密測量技術和可互換零件的概念，人類歷史上首次實作了機器的設計、制造和批次生產。
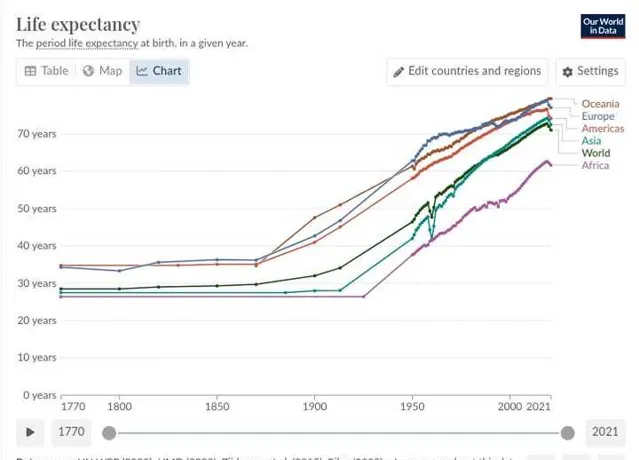
從預期壽命、兒童和母親死亡率等角度比較工業革命前後的人類生活品質。
範例回答：工業革命之前，社會中只有少數精英掌握著絕大部份財富，而普通民眾則生活貧困，壽命短暫。工業革命後，科學和工業的進步顯著提高了人類的平均壽命，同時大幅降低了兒童死亡率。
資本主義制度、公司組織形式，以及私有財產制度和政府對權利的保護，如何促進了人與人之間的正和賽局式互動。
範例回答：公司允許多人聯合起來，建立能夠超越個人能力的組織。資本主義與權利保護使得人們能夠投資未來。這些力量的結合，使得人們能夠構建未來報酬豐厚的事物，透過創造新的財富來源幫助人們積累財富。
人類是如何成功解決過去的重大問題的，例如脊髓灰質炎疫苗的研發、農業綠色革命、哈伯-博世氨合成工藝、臭氧層空洞問題、酸雨治理等
範例回答：你無法像很久以前那樣，每英畝地養活很多人。人們開始使用蝙蝠糞便作為肥料，但蝙蝠糞便有限，它們快要用完了。哈伯-博世工藝應運而生，它從大氣中提取氨來制造肥料，從而拯救了無數免於饑餓的生命。
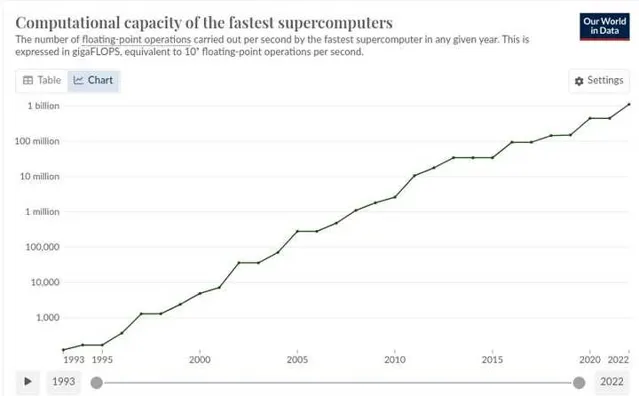
從工業革命到莫耳定律，理解進步的指數性質
範例回答：一旦達到一定程度的進展，你就可以利用這些進展取得更大的進步，因此進展會隨著時間推移而復合增長。莫耳定律，即利用更快的電腦來制造更快的電腦，就是這一現象的例證。
人類偉大工程巡禮：從三峽大壩、青藏鐵路到南水北調工程和載人航天工程
範例回答：人類真是太棒了！我們創造了許多令人驚嘆的傑作，比如三峽大壩，它不僅發電，還防洪、航運，造福無數人。更不可思議的是，我們修建了青藏鐵路，這條世界上海拔最高、路線最長的高原鐵路，讓「世界屋脊」與內地緊密相連！我們甚至實作了載人航天，把中國人的足跡送上了太空！
基礎科學
方法論
動機
「科學」一詞兼具雙重含義：其一是指探索真理的方法論，其二是指透過這種方法論所積累的知識體系。
理解這一方法論是什麽、為何與之前的不同，以及如何在生活的各個方面運用它，對於理解人類如何取得如今的成就至關重要。
合格標準
為透過本課程，學生需要參加一次現場考試，展示對以下內容的理解：
科學的核心：理論必須經過實驗檢驗。換言之，認識世界最有效的方法就是與世界直接互動。
範例回答： 你可以在沙發上冥思苦想很久，但若真想了解這個世界，最終還是得親身去探索和研究。
實驗結果如何隨現實世界的真相而變化
範例回答： 設計實驗時，我們期望能根據現實情況得到不同的結果。例如，要驗證不同重量的物體是否以相同速度下落，你可以同時放下兩個物體並觀察結果；如果它們同時著地，就說明下落速度相同，否則就不同。
當前科學研究的標準流程
範例回答： 科學家們透過收集數據、進行實驗，然後運用統計方法分析數據來驗證假設。盡管數據解讀頗具挑戰性，但科學家們會竭盡全力。隨後，他們會撰寫一篇詳細闡述研究過程的論文，送出給同行評審。最終，論文會在學術期刊上發表。
對證據的機率性理解，以及證據與證明之間的區別
範例回答：證據能夠增加某事發生的可能性，但這種可能性的增加程度取決於你原本對獲得證據的預期。舉個例子，如今人人隨身攜帶相機，那麽假如大腳怪真的存在，我們理應期望有人能拍到一張清晰的照片。然而事實是，至今沒有人拍到，這就成了大腳怪不存在的證據。不過，要註意的是，證據並不等同於證明。證據只是增加或減少某事的可能性，而證明則是確鑿無疑的。
為什麽預測未來比解釋過去更能有效檢驗知識水平
範例回答： 如果你進行一項實驗而未做出預測，那麽你大可聲稱你預料到了所發生的一切，並以此證明你一直是對的。但若你公開做出預測或打賭，那麽當你出錯時，便無法逃避責任；你必須直面你的信念與事實不符的現實。
相關性與因果關系
範例回答： 假設我們經常發現兩件事同時出現，比如財富和教育水平。它們
相關
。這是否意味著一個導致了另一個呢？嗯，存在多種不同的可能性。如果 A 和 B 相關，那麽可能性包括：
A 導致 B
B 導致 A
其他因素 C，導致了 A 和 B 的發生
它們同時出現純屬偶然
你必須做實驗才能知道哪個是真的。
基礎資訊素養
動機
人類如今所處的資訊環境，與我們在前進演化過程中所適應的環境有著天壤之別。它與人類歷史上絕大多數時期的環境都截然不同。即便與短短二十年前相比，現在的資訊環境也已經發生了翻天覆地的變化！
在這樣一個環境中遊刃有余是一項關鍵技能，它不僅關乎如何在紛繁復雜的世界中自如行走，更是學習本身的必備條件。我們該如何辨別哪些資訊是可信的？如何區分事實與觀點？
同時，為孩子們應對社交媒體做好準備也至關重要。雖然我個人更希望避開社交媒體，但我認為，完全禁止使用社交媒體的做法，可能會像過去那種老套的禁欲教育一樣收效甚微。
合格標準
要順利透過本課程，學生需要參加現場考試，證明自己理解了以下內容：
事實與觀點
範例回答：事實是確實發生的事情或可驗證的客觀現實，而觀點則是人們對這些事實的
感受
和看法。事實不等同於觀點，觀點也不等同於事實。
地圖不等同於領土
範例回答：人們
相信
的和客觀
事實
之間常常存在差異。有時兩者一致，有時卻大相徑庭。每個人的頭腦中都有一套關於世界的信念和認知模型，但這些信念和模型可能與現實不符。不同的人面對同一個
領土
（即客觀存在的現實世界）時，可能會在頭腦中形成不同的
地圖
（即對現實的理解和認知）。
媒體更註重娛樂性，而非真實性
範例回答：新聞頻道、報紙和其他新聞來源實際上並不會因報道真實、客觀的事實而得到獎勵或受到懲罰。它們和其他企業一樣，首要目標是盈利，因此它們追求的是受眾參與度。為了獲得更多點選量和點贊，它們可能會不顧真實性釋出吸引眼球的內容。這並不意味著媒體總是在撒謊，但也不能保證它們始終在如實報道真相。
社交媒體如何扭曲真相
範例回答：在社交媒體上，人們傾向於只展示自己最好的一面，精心挑選值得炫耀的內容。其他人也是如此。這就意味著，當你看到某人在社交媒體上的生活似乎非常精彩時，你看到的只是他們生活的精華部份，而非完整的現實圖景。同樣，當你看到許多人似乎比你更成功時，不必感到沮喪或自卑——他們表面上的成功並不意味著你的生活就更糟糕。
如何研究一個主題
範例回答：假設我想了解更多關於某事物的資訊，比如苔蘚。我可以使用谷歌或其他搜尋引擎進行搜尋，在維基百科上閱讀相關內容，或者向大語言模型詢問。交叉驗證這些資訊來源是個好主意，因為其中某些資訊可能存在錯誤，尤其是在話題具有爭議性時。
如何改變自己的想法
範例回答：隨著你獲取更多資訊，改變對事物的看法是很自然的。這很好！你應當始終保持開放心態，因為總有可能你之前的看法是錯誤的。如果你從不改變想法，那麽你對新資訊毫無反應——這意味著你可能更像一塊石頭，而非一個活生生的人。人會變，石頭不會。
基礎經濟學
動機
我遠非經濟學專家，但我可以告訴你什麽是供需，以及它們為何重要。我可以談論供需的彈性，以及它通常如何決定稅收負擔的歸屬。我可以告訴你價格上限和下限對市場的影響。
我可以告訴你市場為何運作，以及為何這至關重要。
這不應該是某種精英知識。它不應該隱藏在大學課程背後。這實際上是我們整個經濟運作的框架。
這應該在每所學校教給每個孩子。
課程將圍繞此圖展開：
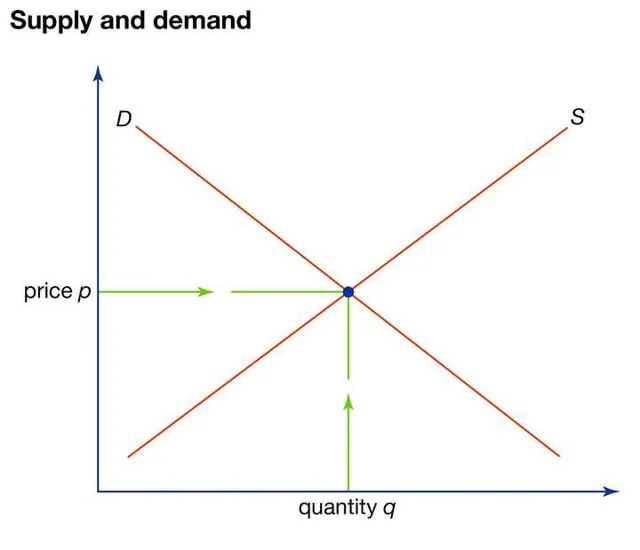
目前已有眾多基礎經濟學課程，因此將這些課程調整到適合第 2 階段學生（大約 10-13 歲）的水平應該不會太困難。需要註意的是，學生的入學並不嚴格按照年齡劃分——如果他們需要更大的年齡才能理解這些概念，那也無妨。課程不需要涉及太多數學知識——實際上，除了理解上面的圖表外，幾乎不需要用到任何數學。
合格標準
為了透過這門課程，學生需要參加一次現場考試，展示對以下內容的理解：
供給、需求與價格均衡
範例回答：供給和需求反映了某種商品或服務在不同價格水平下的交易數量。商品的實際價格和生產數量由供需曲線的交點決定，即供給等於需求的均衡點。
供給和需求曲線斜率的成因
範例回答：供給曲線：隨著生產規模擴大，邊際成本上升，因此價格上漲。需求曲線：商品價格上漲時，需求量減少；價格下降時，需求量增加。
供給和需求彈性的含義
範例回答：彈性衡量的是對價格變化的敏感程度。需求彈性：對於非必需品，如電影票，價格上漲會導致需求顯著下降。但對於必需品，如住房，即使價格上漲，需求變化也相對較小。供給彈性：取決於增加一單位產量的邊際成本。例如，新建一棟房屋成本高昂，供給彈性低；而復制一份視訊遊戲成本很低，供給彈性高。
價格下限和上限的影響
範例回答：價格下限是某物可以出售的最低價格，高於沒有下限時的價格。這就像最低薪資，會導致供過於求，因為供應量大於需求量。價格上限是某物可以出售的最高價格，低於沒有上限時的價格。這就像租金管制，會導致短缺，因為需求量固定在高於供應量的水平。
稅收負擔所在及其影響
範例回答：稅收落在那些無法逃避它們的人身上。如果所有商品在銷售時都被征稅，比如銷售稅，那麽人們只需支付更高的價格，稅收就落在消費者身上。另一方面，如果只有一家公司被征稅，他們就必須支付，因為如果不支付，他們的商品會變得更貴，人們就不會再購買了。一般來說，你征稅的東西會減少，因為它使商品變得更貴，減少了人們做事情的動機。
為何市場勝過中央計劃
範例回答：市場透過每個人每天各自了解的零碎知識來協調所有人。無論中央計劃者多麽聰明，他們都不可能比所有人加起來更聰明，也不可能知道其他人所掌握的具體資訊。
市場在哪裏會失靈
範例回答：市場失靈發生在未將外部性計入價格時，例如公司可以隨意向河流傾倒廢物。這時政府介入，強制企業將外部性納入價格考量。這就是公地悲劇。
以上內容節選自：
