不考慮空氣阻力時候,二者無論是同體積還是同同重量,到達地面時候速度相同。
而最終坑的大小在於球對地面釋放的能量多少。
分析接觸地面時候,球體會發生彈性形變,這個形變會提供一個向上的力,在一個是地面的阻力,我們把這兩個力合稱為向上阻力吧。還有與周圍土壤接觸時候的摩擦力(這個摩擦力對於另外兩種力來說很小,忽略掉)。
顯然向上阻力與接觸面積有關(接觸面大的話,彈性形變提供的力就大)。
則相同體積情況下,土壤材質相同提供的阻力相同,則坑的大小取決於球的硬度,則木頭顯然比鐵軟,則鐵球砸的坑大。
相同品質情況下,一方面,木球體積變大,接觸面變大,另一方面,木頭比鐵軟,二者都會導致坑變小,則忽略阻力情況下,鐵球坑大(很符合生活常識)。
考慮空氣阻力,我們分析最終速度。(假設到達地面時候重力依然大於阻力)
首先考慮阻力公式。

c為阻力系數,ρ為空氣密度,S為接觸面積,v為相對空氣的速度。其中cρ都是常數,且對於一個已知的物體,顯然S也是一個常數,為了方便,我們記此公式為
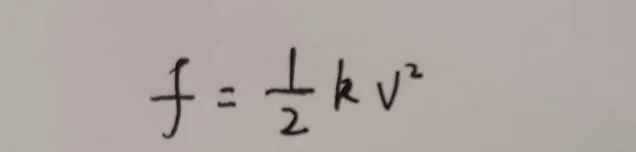
則可列出運動方程式

然而這個微分方程式並不好解,我們換另一種思路,借助動量定理的微碎形式,即dp=Fdt,即dp/dt=F,可以得出

接下來,我們來分析這個解。
首先,可以知道v與t,k都有關,根據常識,有了阻力最終速度一定會比無阻力要小,我們設二者之差為Δv。
而另一方面,k增大會導致物體運動時間延長,我們設這個時間差為Δt,則由動量定理,mg(t₀+Δt)-阻力沖量=mv,其中v為最終速度。而無阻力時,mgt₀=mv₀,v₀為無阻力的最終速度,那麽可知,mgΔt-阻力沖量=mΔv,可見最終Δv的大小與Δt,k有關,Δt與k又有關,最終我們還是要回到對k對t的關系上。
由已知的速度,可得出

我們得到了t關於k的函式式,這裏面由於我們關心的始終是最終的時間大小與最終的速度大小,那麽我們就先把x當做一個常數。這個式子看著非常復雜,如果嚴謹來做的話,那麽就要把v看成k,t的復合函式,其中t=t(k),之後在求出v關於k的偏導數=∂v/∂k+∂v/∂t·∂t/∂k,這會非常復雜。那我們能否定性的去分析呢?
我是這樣考慮的(不知道對不對)

可以看到t近似與k½成正比。那麽帶入到v的運算式(這裏其實是最終速度的大小),求其關於k的導數,得到

那麽我們可以看出,最終的v還與m,k的關系有關。對於同重量不同密度的球,二者S不同,這種情況結果會非常復雜,因為最終還需要考慮接觸面積導致的彈性力的變化問題。但當S相同時,k相同了就如二者最終會歸為最開始討論的無阻力問題。










