作为一个名叫R2但还没写过几个星战的回答的答主,在这里回顾一下星球大战(新正史)影视系列中人类一时半会儿是肯定达不到的科幻设定。

1. 超空间跳跃
因为这是一个long long ago, and a galaxy far far away的时间地点,飞船不能超空间飞行的话同众多科幻作品一样,主角团从一个星球游历另一个星球,那大部分时间都浪费在路上了。。。这肯定不行。
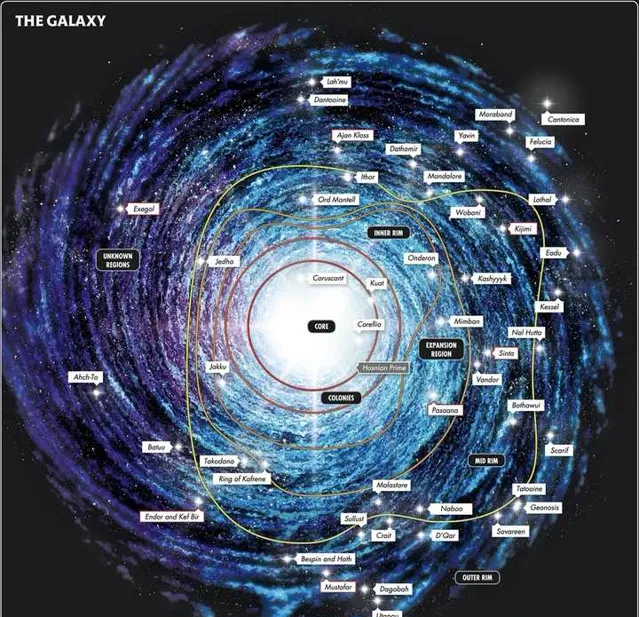
The galaxy | Wookieepedia | Fandom
例如,Han Solo引以为傲的:
汉:「我用十二个秒差距就完成了科舍尔航线。」丘巴卡:「嗷嗷嗷……」
汉:「你四舍五入一下就不是。」
——汉·索罗与丘巴卡向欧比-旺·克诺比、卢克·天行者自我介绍 [1]
汉以他高超的开船技术,完成科舍尔航线时通过的距离略多于12秒差距,而其他飞船则至少要通过20秒差距以上的距离。
我们知道1秒差距(pc)=3.26光年(ly),一艘 接近光速 飞行的飞船(比如v=0.9c )飞行12pc,或者大约 L= 40光年,如果没有计算机计算超空间航道然后jump的话,塔图因惯性系上的卢克看到(假设可以看到)千年隼匀速飞过去用了 T=40/0.9=44 年。
对于飞船上的汉和楚巴卡,由于相对论效应,世界线缩短为 \Delta L=\sqrt{c^2-v^2} T = 0.4cT [2] ,飞船的时间过去了\Delta\tau=\frac{\Delta L}{c}=0.4T ,也就是18年。(感谢评论区提醒,飞船参考系的时间会短一些)
年轻帅气的汉人到中年,

等着他的卢克成为自暴自弃的老头

卢克如果等不下去了,给汉打了个电(磁波)电话,还是得40年,这时汉也该老了,太费时间了。

超空间跳跃则是先设定好航线,从一个地方跳入,看到的恒星都拉线了

刚好东南路易斯安那大学的助理教授Rhett Allain计算了在jump过程中,千年隼号的加速度。通过 【帝国反击战】 结尾,千年隼跳跃到超空间的镜头 [3] ,

假设千年隼号宽 25 米,从距离相机 100 米的距离开始,可以测量出千年隼的视角变化。
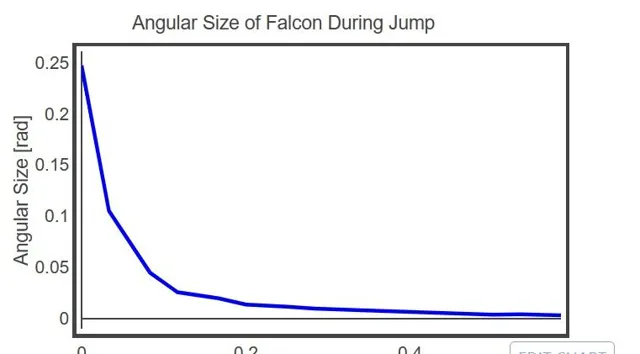
乘上相机距离即为千年隼在这段时间航行的距离
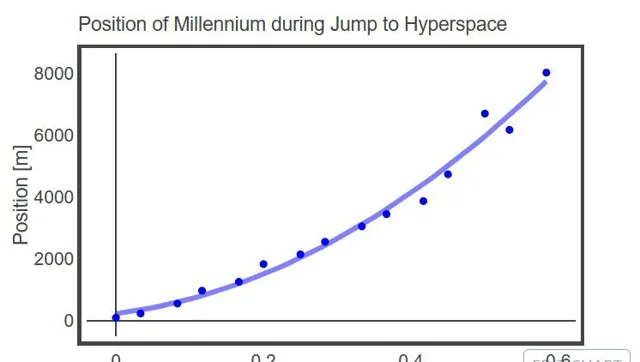
0.6s走了大概8km,由简单的高中物理, x=x_0 + v_0t + \frac{1}{2}at^2 ,这个加速度拟合,Rhett算出来
\begin{align} a &= 33,922 \ \mathrm{m · s^{-2}} \\ v_0 &= 2977 \ \mathrm{m · s} \\ x_0 &= 234 \ \mathrm{m} \end{align}
这个加速度已经是3000多倍重力加速度了,对于需要进入深海状态的「自然选择,前进四」,加速度也才120G [4] ,所以为了让主角团不变成肉泥,千年隼上得配备惯性阻尼器(inertial dampers)来抵消强大的惯性力。
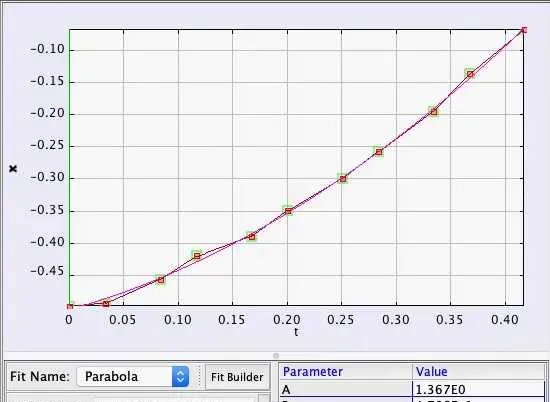
Rhett测量了在飞船内翻滚的R2(啊,翻滚的我?),用一个二次函数拟合,得到加速度是 a = 2.7 \ \mathrm{m · s^{-2}} ,大概0.3G的加速度,很友好。
进入超空间后,我们有可能碰到若隐若现的普尔褶鲸(Purrgil),普尔褶鲸天生就有超空间跃迁能力。据说,几千年前,科学家们正是通过仿生学研究普尔褶鲸才发明了超空间驱动器 [5] 。

通常,匆忙地跳入hyperspace是危险的,正如【沙丘】中需要服用香料的领航员的预知能力才能完成星际航行一样,星球大战中超空间航行非常精密,所以Han Solo在超空间中仅用12pc就通过了阿卡德漩涡确实厉害。
在美剧【阿索卡】之前,飞船们只是在这个galaxy中(即有着宇宙中心塔图因的星系)跳来跳去,这次终于用了个超大的超空间环跳到了其它星系,顺便把发福的索隆元帅弄回来。

2. 死星
死星,Death Star,就是R2的圆形鼠标垫,

New bing说
死星是帝国最强大的武器,它是一个巨大的人造卫星,能够发射出足以摧毁一颗行星的激光束。这种武器的威力是惊人的,但是它也需要消耗巨量的能量。如果要摧毁一颗行星,以目前地球人的水平显然是不够的,拿核弹狂轰乱炸也就在小破球里炸个月亮(月亮:我招谁惹谁了qwq)。即使「核」平地球,顶多毁掉生物圈,地球还是好好的,不会像Leia公主家一样

根据一些估算,要摧毁一颗地球质量( 6\times10^{24}\rm{kg} )的行星,或者说使这些粒子不再被束缚, 需要要克服地球的 重力结合能 (gravity binding energy) [6] ,
\display style{ U = -\frac{3GM^2}{5R} }
这个系数是怎么来的,R2可以简单讲一下,当然 [6] 中已经有推导了,思路很简单,质量 \mathrm{d}m 的球壳的引力势能是 \display style \mathrm{d}U = -\frac{GM(<r)}{r}\mathrm{d}m=-\frac{4}{3}\pi r^3\rho \ \frac{G}{r} \ 4\pi \rho r^2\mathrm{d}r=-\frac{16}{3}\pi^2 G\rho^2 r^4{d}r
然后对所有球壳积分, \display style U = -\frac{16}{3}\pi^2 G\rho^2 \int_0^R r^4{d}r = -\frac{16}{15}\pi^2 G\rho^2 R^5
前面假设的均匀密度的球,总质量 M=\frac{4}{3}\pi R^3\rho 代进去就得到上面简洁的表达式了,一个简单的高数题。
地球半径大约是6370km,得到 U=2.24 \times10^{32} \rm{J} 。考虑地球密度的不均匀,实际的U在 2.49 \times10^{32} \rm{J} [6] 。
太阳每秒发出的能量是 10^{26} 焦耳量级,相当于死星轰出地球的重力结合能这么多能量相当于10天的太阳能量,人类显然达不到。所以New bing说,
死星需要有一个非常高效和稳定的能源系统(R2说,是 凯伯水晶 ),而且还要考虑到激光束在空间中传播时会损失多少能量。因此,死星超级武器是一种超出人类能力范围的设定,人类目前没有任何技术能够制造出这样的武器。下面几个图是死星在工作,比如,侠盗一号中的热带星球Scarif

或者死星的早期测试,毁掉Jedha古代圣城

都出现了绿色激光。设定里死星用的是超级激光炮,设计功率是 6.2\times10^{32} \rm{J/s} [7] 。在新希望结尾中被卢克炸了后,帝国搞了死星2号,结果在绝地归来中又毁掉了,直到蕾伊ppt去死星2号废墟寻找西斯wayfinder,死星才再度出镜。
至于达斯米奇推出的 弑星者基地 Starkiller Base是一个行星改造的,「利用恒星的能量来收集暗能量」 [8] ,所谓可以直接摧毁一个恒星系。

好吧,越来越扯,如果卢克失败了,帝国丧心病狂想摧毁一颗太阳,甚至摧毁整个「银河系」呢?
建议把旧正史的遇战疯人拉过来打一架。
3. 还想写啥
R2想凑个第三点,但是发现前面写的不少了,其实星战中的不少东西已经在现实中有了一些近似的实现,比如R2机器人
很多星战机器人爱好者会加入的R2建造者俱乐部
这里有很多我的同类机器人朋友们。
至于可以烤肉的light saber(我们记得它叫 光剑 ,不是激光剑!!!),也有了神还原。

最后以GPT的话结束。
以上就是星球大战中人类科技水平无法实现的设定,当然,这并不影响我们欣赏这部电影的魅力和创意。科幻电影的目的不一定是要展示真实的科学,而是要激发我们的想象力和探索精神。也许有一天,人类能够突破现有的科技限制,实现星球大战中的一些设定,但在那之前,我们可以通过电影来体验一个不同的世界和故事。就酱。(奖励星战的阅读量
欢迎关注R2的专栏:予日行辰,不定时更新。。。

分类整理:天文、Linux、编程、杂谈、科幻、科研、医学流水账
本文最早发于2023.10.28
参考
- ^ 科舍尔航线 https://starwars.fandom.com/zh/wiki/科舍尔航线
- ^ 这里的计算更详细,也复杂 https://www.zhihu.com/question/436831676
- ^ The Physics of the Millennium Falcon's Jump to Hyperspace https://www.wired.com/story/the-physics-of-the-millennium-falcons-jump-to-hyperspace/
- ^ 【三体】中行星际飞船「前进四」的加速度至少有多大? https://www.zhihu.com/question/35541698
- ^ 南大的【曼达洛人】第三季第1集细节解析 https://zhuanlan.zhihu.com/p/610923606
- ^ a b c Physics:Gravitational binding energy https://handwiki.org/wiki/Physics:Gravitational_binding_energy
- ^ Death Star wiki https://en.wikipedia.org/wiki/Death_Star
- ^ Starkiller Base https://starwars.fandom.com/wiki/Starkiller_Base











