这篇文章想和大家分享一下Apollo 6.0中的参考线平滑算法。参考线平滑模块在Apollo的框架中占据着非常重要的位置,我之前很长一段时间也都没有给予其足够的重视,在实际调试Apollo的这套算法时,才发现其重要性,因此这次想深入解析下该模块。
一、参考线平滑的整体框架
在Apollo的路径规划中,其采用的是基于Frenet坐标系下的规划算法,因此非常依赖于道路中心线的平滑性。而实际工程中,高精地图给出的道路中心线的平滑性往往都不能满足规划模块的需求,因此规划中是不能拿来直接用的,需要对其进行平滑操作。参考线平滑在Apollo项目下的/apollo/modules/planning/reference_line路径中,里面包含了多种参考线平滑算法,整体框架结构如下所示。
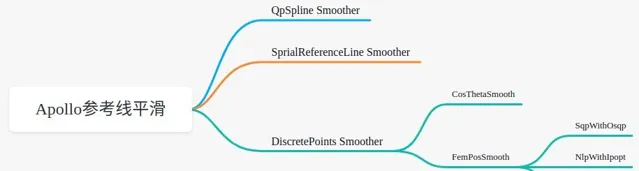
目前Apollo中共有三种参考线平滑算法,分别为:
- QpSpline Smoother
- SpiralReferenceLine Smoother
- DiscretePoints Smoother
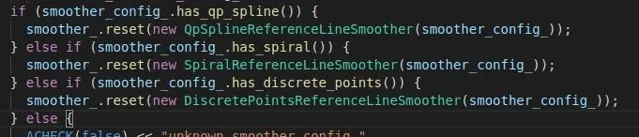
通过配置参数可以选择需要采用的参考线平滑算法,目前Apollo中默认配置为最后一种,基于离散点的平滑,这篇文章也就针对该算法进行讲解。
参考线的平滑函数如下图所示,可以看出该函数的输入为原始raw_reference_line,输出为平滑后的smoothed_reference_line,整体的输入输出很简洁。
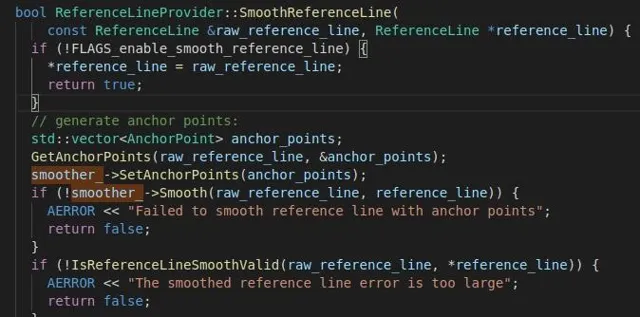
二、设置中间点anchor points
首先第一步就是根据原始的reference_line来选取中间点,其实这一步就是根据reference_line的s值进行采样,采样的间隔为0.25m。采样完毕后,就能得到一系列的ref_points,而每个anchor_point就包含了一个ref_point以及横纵向的裕度。
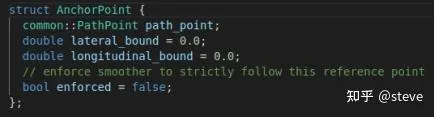
横纵向裕度的默认参数为:
longitudinal_boundary_bound : 2.0
max_lateral_boundary_bound : 0.5
min_lateral_boundary_bound : 0.1
然后再根据自车宽度,车道边界类型(是否为curb)等再对横向裕度进行收缩。AnchorPoint结构中的enforced变量表示该点是否为强约束,在参考线平滑中只有首尾两点为强约束。
计算完anchor points后,将其赋值到smoother对象中。
三、smooth函数
接下来就是参考线平滑中的主体部分,即smoother类下的smooth函数,这里我只介绍Apollo 6.0中目前配置参数里正在使用的discrete_points_reference_line_smoother下的smooth函数。 该方法通过对原始参考线上的离散点的有限偏移对原始参考线进行平滑。 可以看到的是,在这个类中还有两种不同的平滑算法,分别是:
- CosThetaSmooth
- FemPosSmooth
实际使用的算法在配置参数里设定,目前Apollo中用的为FemPosSmooth该算法,后面介绍代价函数时我会展开来讲下这两种方法的区别。
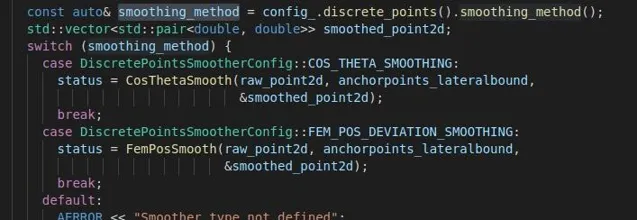
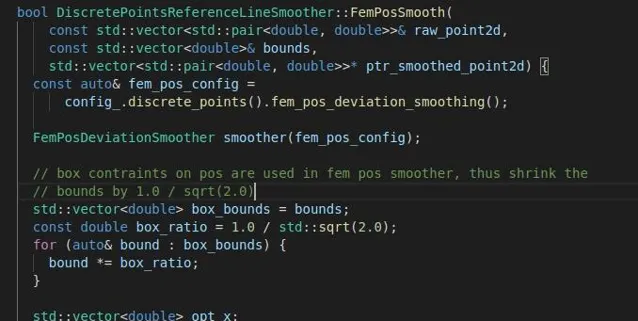
从该函数的入参可以看出,输入为anchor_points的x,y值以及横向裕度,输出为平滑后的point2d。可以看出这个函数里也没做什么重要的事,只是一个接口,先是将横向的裕度进行了收缩,然后就直接调用了Solve函数进行问题求解。
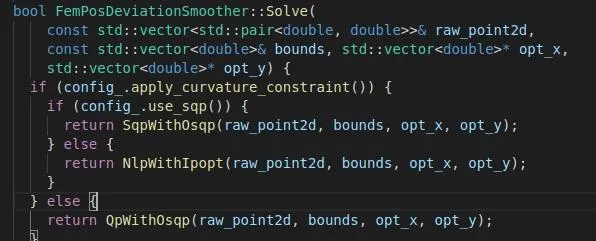
进入到Solve函数后,我们可以看到这里又有三种求解方式(从中可以看出参考线平滑模块还是非常庞大的,也说明了其重要性),这分别是利用不同求解器实现了这个方法。如果考虑参考线的曲率约束,其优化问题是非线性的,可以使用ipopt非线性求解器求解(内点法),也可以将曲率约束线性化后使用osqp求解器来用SQP方法求解;如果不考虑曲率约束,则直接用osqp求解二次规划问题。目前Apollo 6.0中默认的参数为不考虑曲率约束,这点我有点奇怪,可能是为了算法效率方面的考虑,也可能是加入曲率约束会使得问题很难求解。后面这三种求解方式我都会介绍一下。
四、优化问题的构造及求解
首先讲解Apollo中默认采用的平滑算法,这里将参考线平滑构造成了一个二次优化问题,并使用osqp求解器进行求解。二次优化问题的整体框架我想大家应该都比较熟悉了,这里直接来看它的代价函数及约束条件。
- 优化变量
离散点坐标(x_k, y_k)
2. 代价函数
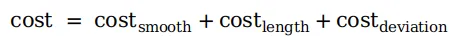
数学表达式如下所示:

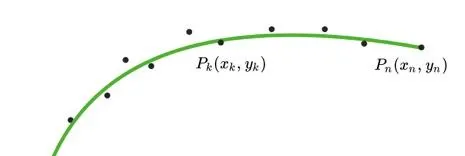
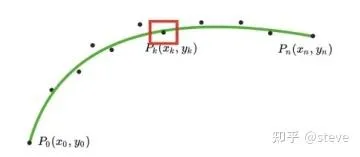
cost_smooth的物理意义可以理解为前后两点连接向量的模平方,如下图中的红色向量P1P3的模平方。如果这三点在一条直线上,则这个值最小,相对应的参考线也越平滑。
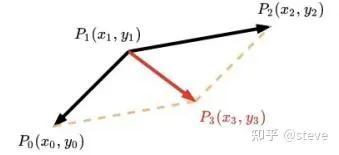
关于这项平滑度的代价,还存在其他的表示形式,例如下图所示的相邻向量之间的夹角theta。

假设我们拥有连续3点P0,P1,P2,其中向量P0P1和向量P1P2之间的夹角就可以表示为:
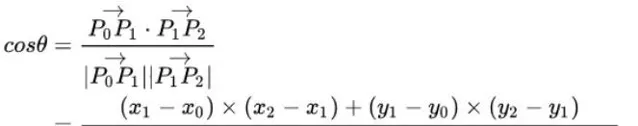
cos(theta)的值越大,theta越小,P0,P1,P2也就越接近直线,参考线也就越平滑。因此cost_smooth也可以表示为:
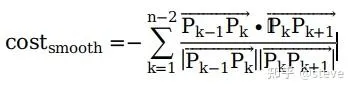
这两种代价函数的表达形式也分别代表了上面提到的参考线平滑中的FemPosSmooth方法和CosThetaSmooth方法。可以看出后一种的cost设定为非二次型函数,因此如果采用这种方法则需要使用非线性优化。
cost_length 代表了离散点之间的距离平方之和
cost_deviation 代表了平滑后的离散点相对原始参考点的偏移距离平方之和
在Apollo的代码注释中,用了6个点作为例子来展示P矩阵的具体形式,大家可以试着按照上面的公式来列出6点的代价函数来看看,就是其注释中的这种形式。
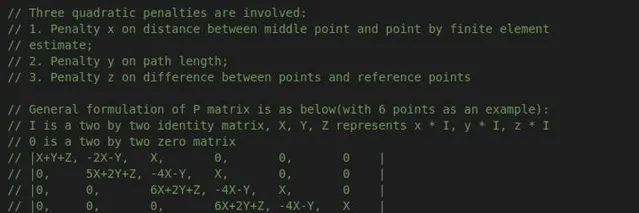
这边还需要提到的是,如果采用的非线性优化来求解该问题,Apollo还增加了一个关于松弛变量的cost,松弛变量的作用在后面的曲率约束中可以看到。
3. 约束条件
第一个约束,我们希望平滑后的参考线距离原始参考线的偏移量不能太大,虽然在代价函数中,已经有了关于偏移量的惩罚项,但这只是一个软约束,不能保证其偏离的具体数值能限制在某个范围内。因此这里我们添加关于偏移量的硬约束,而这里的偏离范围就是之前设置的横纵向裕度构成的box内。
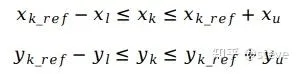
在非线性优化算法中,Apollo还加入了曲率的约束。关于曲率的计算,Apollo的主要思想是三点构成一个圆来求解半径,并且中间也设置了几个假设:
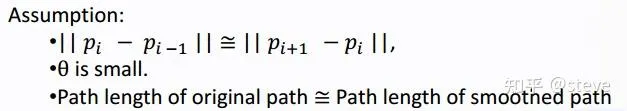
最终约束条件的构成计算为:
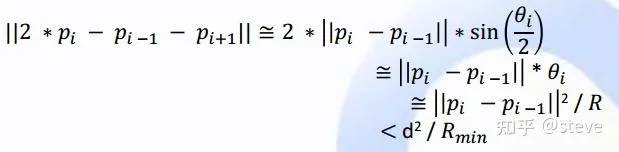
第一个近似是假设了前后两段的长度近似相等,也就是第一个假设;
第二个近似是假设了theta值很小时,sin(theta)约等于theta;
第三个近似表示两点间的弧长,约等于两点间的距离,也就对应了第三个假设。
这里的数学推导不是很复杂,大家可以画图出来看看就明白了。最终这个约束的上限为设定的最大曲率,即最小转弯半径。d表示离散点之间的平均长度,Rmin表示最大曲率约束。
为了保证有解以及求解更快的收敛,Apollo中还添加了大于0的松弛变量,因此最终的曲率约束可以表示为:
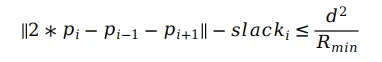
对于松弛变量,只需要保证其大于等于0即可:
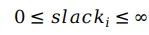
4. 曲率约束的线性化
到此优化问题的基本形式已经完全建立了,我们可以发现代价函数为标准的二次型,而约束条件里唯有曲率约束是非线性的,也就意味着不能当成二次优化问题来求解。我们当然可以把其当做一个非线性优化问题来使用Ipopt进行求解,也是Apollo里采用的一种做法。或者我们可以单独将这项曲率约束线性化,这样也就将这个问题转变为了二次优化问题,即可使用osqp进行求解,而这在Apollo里对应着SqpWithOsqp算法。
曲率约束的线性化也比较简单,直接在参考点处进行泰勒展开即可。
假设我们的约束方程为:
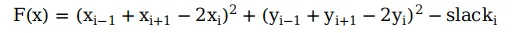
在原始参考点X_ref处对其进行泰勒展开后得:
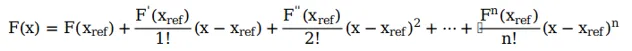
线性化只保留第一项得:
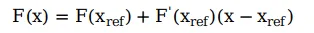
F在原始参考点X_ref处的值为:

在F(x)原始参考点x_ref的导数为:
其中:
带入曲率约束方程并化简后得:
五、总结
至此,Apollo中基于离散点算法的参考线平滑模块就全部介绍完了。整个模块涉及到的规划算法还是比较经典的,其主要思想都是建立在优化问题上,需要一定的规划算法和优化基础来充分理解其核心。当然Apollo的算法也不是完美的,在我们实际工程中,还需得根据实际场景来调整它的代价函数和约束条件,以达到更好的效果。欢迎各位读者在评论区留下你们的问题及思考,大家互相交流,共同进步~ 也非常欢迎各位关注我,留言讨论~
参考资料:
- 开发者说丨离散点曲线平滑原理
- steve:Apollo 6.0 规划模块算法解析2
- apollo 参考线平滑
- 百度Apollo代码阅读:参考线平滑FemPosDeviationSmoother_荔江北的博客-CSDN博客_apollo 参考线平滑











