卡尔曼滤波在智驾中应用广泛,从传感器检测的跟踪到多传感器的信息融合,从单一传感器定位信息的滤波到多传感器融合定位,从传统检测算法到深度学习的后处理,都少不了卡尔曼滤波的身影。本文以基础卡尔曼滤波器的应用举例,试图从整体框架和应用方面对卡尔曼滤波有个整体的理解,解决如何使用和使用过程中数据的分析解读问题。
1. 整体介绍
全文以激光雷达对一个行人的检测结果为输入数据,构建卡尔曼滤波器对其检测结果进行滤波,调整关键参数,直观感受关键参数对滤波结果的影响。整体思路如下:
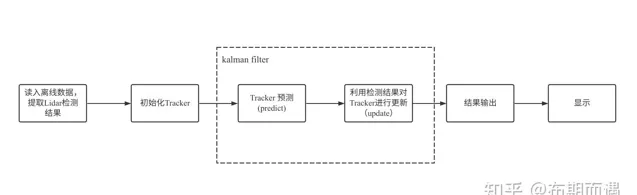
该开源数据中包含激光雷达和毫米波雷达两个传感器同时检测的结果,因此需要从中提取出Lidar的检测。通常我们detect或measurement来表示传感器的检测,用tracker表示经过卡尔曼滤波后跟踪或滤波的结果。基卡尔曼滤波总体可以分为两个部分:predict和update。其中predict接收上一时刻的tracker,将其预测到当前时刻下;update 接收measurement对predict得到的tracker进行更新,具体后面会详细介绍。
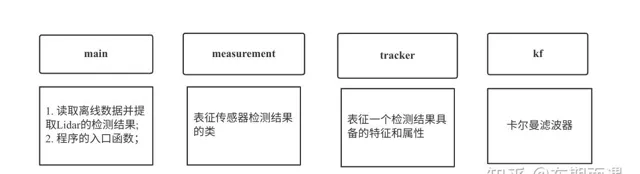
如图2所示,文中会涉及到四个文件或类,分别是:函数的入口main, 处理检测的measurement, 处理检测结果的tracker, 进行滤波的kf。
2. 数据导入
数据保存在 obj_pose-laser-radar-synthetic-input.txt 中 [1] ,一个行人在前面行走,一辆搭载了激光雷达和毫米波雷达的智能车辆对其进行持续的检测。数据如图3所示,该数据中包含了激光雷达和毫米波雷达的检测结果,第一列的L表示该行是Lidar的数据,R表示行是Radar的数据。每行的第二列为传感器检测到的目标X坐标,第三列为Y坐标,第二列之后的数据本文暂不使用。

/* 以下为main.cpp的导入数据部分 */
// 路径为放置obj_pose-laser-radar-synthetic-input.txt文件的路径
std
::
string
file_name
=
"obj_pose-laser-radar-synthetic-input.txt"
;
std
::
ifstream
in_file
(
"路径/obj_pose-laser-radar-synthetic-input.txt"
);
if
(
!
in_file
.
is_open
())
{
std
::
cout
<<
"can not open input file: "
<<
file_name
<<
std
::
endl
;
}
int
i
=
0
;
std
::
string
one_line
;
// measurement类用于存放检测结果,每一个检测由时间戳timestamp,传感器类型sensor_type,检测数据x,y组成
std
::
vector
<
Measurement
>
measurement_list
;
// 每次读取一行数据,其中i用于控制读取数据的行数
while
(
getline
(
in_file
,
one_line
)
&&
(
i
<=
10
))
{
std
::
istringstream
iss
(
one_line
);
Measurement
one_frame_data
;
std
::
string
current_sensor
;
// 读取一行中的第一个数据,也就是R或L
iss
>>
current_sensor
;
// 仅使用L的数据
if
(
current_sensor
.
compare
(
"L"
)
==
0
)
{
//一个检测的sensor_type
one_frame_data
.
sensor_type_
=
Measurement
::
lidar
;
float
x
;
float
y
;
iss
>>
x
;
iss
>>
y
;
one_frame_data
.
sensor_measurment_
=
Eigen
::
VectorXd
(
2
);
// 一个检测xy坐标,构成一个二维的向量
one_frame_data
.
sensor_measurment_
<<
x
,
y
;
// 一个检测的时间戳
iss
>>
one_frame_data
.
timestamp_
;
// 将整帧数据放到所有的测量中
measurement_list
.
push_back
(
one_frame_data
);
}
else
if
(
current_sensor
.
compare
(
"R"
)
==
0
)
{
continue
;
}
// i++; //当需要控制读取行数时打开
}
3.单帧数据的处理
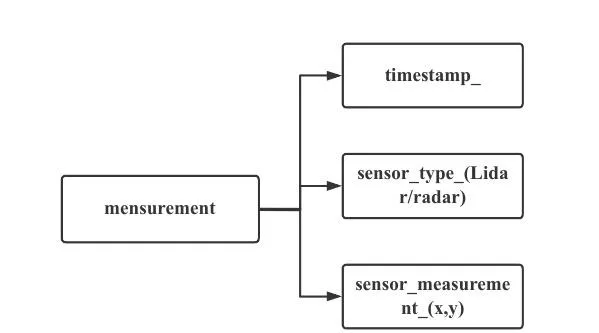
读取的一帧帧数据依次存放到measurement_list中,每一帧的数据格式如图4所示。
/* measurement.h */
#ifndef MEASUREMENT_H_
#define MEASUREMENT_H_
#include<stdint.h>
#include"Eigen/Dense"
class Measurement
{
public:
int64_t timestamp_;
enum SensorType
{
lidar,
radar
}sensor_type_;
Eigen::VectorXd sensor_measurment_;
};
#endif
下面对每一帧的数据进行处理,除第一次处理需要初始化外,其他帧直接进入处理过程,处理过程主要由predict和update两步组成。
(1)tracker的初始化
tracker的初始化只在第一帧时发生,主要分为两个部分,一个是卡尔曼滤波器相关参数的初始化,该类参数不依赖检测数据,可直接在tracker新建的时候直接生成,例如测量矩阵H,状态协方差矩阵P,测量噪声矩阵R,状态转移矩阵F; 第二类是与检测相关的状态参数,状态量x,y,time_stamp.
tracker::tracker(){
kf_filer_.H_ = Eigen::MatrixXd(2,4);
kf_filer_.H_<< 1, 0, 0, 0,
0, 1, 0, 0;
kf_filer_.P_ = Eigen::MatrixXd(4,4);
kf_filer_.P_ << 1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1000, 0,
0, 0, 0, 1000;
kf_filer_.X_ = Eigen::VectorXd(4);
kf_filer_.R_ = Eigen::MatrixXd(2,2);
// kf_filer_.R_ << 0.0225, 0,
// 0, 0.0225;
kf_filer_.R_ << 2, 0,
0, 2;
kf_filer_.F_ = Eigen::MatrixXd(4,4);
state_.timestamp = 0;
}
第一类的参数初始化放到了tracker中,下面具体来看各参数的初始化取值:
\left(\begin{array}{ccc} 1&0&0&0\\ 0&1&0&0\end{array}\right)*\left(\begin{array}{cc|c} x\\ y\\ vx\\vy\end{array}\right) = \left(\begin{array}{cc|c} x\\ y\end{array}\right)
x_{t}=\left(\begin{array}{ccc} 1&0&dt&0\\ 0&1&0&dt\\0&0&1&0\\0&0&0&1\end{array}\right)*x_{t-1}
第二类参数的初始化可直接将第一帧传感器的检测结果传入
/* main.cpp中处理部分 */
// 新建一个tracker
tracker tracking;
for(size_t i=0; i<measurement_list.size(); i++)
{
//初始化: 只有当第一次运行时进行
if(i==0)
{
// 将第一帧的数据传入到tracker所绑定的卡尔曼滤波器中
tracking.kf_filer_.X_ << measurement_list[0].sensor_measurment_[0],measurement_list[0].sensor_measurment_[1],0,0;
tracking.state_.timestamp = measurement_list[0].timestamp_;
continue;
}
// 传入检测数据,利用process_measurement函数处理每一帧
tracking.process_measurement(measurement_list[i]);
std::cout <<"X: " <<tracking.kf_filer_.X_.transpose() << std::endl;
//std::cout <<"P: " <<tracking.kf_filer_.P_ << std::endl;
}
(2)predict

如图5所示,卡尔曼滤波的过程主要由两部分组成,一个为predict,一个为update:
/* tracker.cpp 中process_measurement */
void tracker::process_measurement(const Measurement &measureTem)
{
// predict
float deltaT = (measureTem.timestamp_ - state_.timestamp) / 1000000.0;
kf_filer_.F_ << 1, 0, deltaT, 0,
0, 1, 0, deltaT,
0, 0, 1, 0,
0, 0, 0, 1;
CalQ(measureTem.timestamp_);
kf_filer_.predict();
state_.timestamp = measureTem.timestamp_;
//update
Eigen::VectorXd z(2);
z << measureTem.sensor_measurment_;
kf_filer_.update(z);
}
其中的predict()和update()为标准的卡尔曼滤波器公式,可单独抽象在kf这个类中:
/* kf.cpp */
void kf::predict()
{
X_ = F_ * X_;
//std::cout << "Q: " << Q_ << std::endl;
P_ = F_ * P_ * F_.transpose()+Q_;
}
predict中的两个公式:主要需要进行F矩阵和Q矩阵的计算,F矩阵在(1)中已经进行了解释,
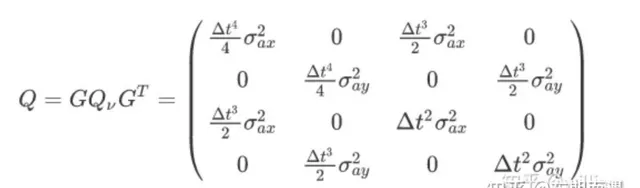
void tracker::CalQ(int64_t timeTem)
{
float deltaT = (timeTem - state_.timestamp) / 1000000.0; //ms to s
float deltaT2 = deltaT * deltaT;
float deltaT3 = deltaT2 * deltaT;
float deltaT4 = deltaT3 * deltaT;
float noise_ax = 3;
float noise_ay = 3;
Eigen::MatrixXd qTem(4, 4);
qTem << deltaT4 * noise_ax / 4.0, 0, deltaT3 * noise_ax / 2.0, 0,
0, deltaT4 * noise_ay / 4.0, 0, deltaT3 * noise_ay / 2.0,
deltaT3 * noise_ax / 2.0, 0, deltaT2 * noise_ax, 0,
0, deltaT3 * noise_ay / 2.0, 0, deltaT * noise_ay;
kf_filer_.Q_ = qTem;
}
(3)update
update的过程比较简单,直接调用标准的卡尔曼滤波公式。
/* kf.cpp */
void kf::update(const Eigen::VectorXd &z)
{
Eigen::VectorXd z_pred = H_ *X_;
Eigen::VectorXd y = z - z_pred;
Eigen::MatrixXd S = H_ * P_* H_.transpose() + R_;
Eigen::MatrixXd K = P_ * H_.transpose() *S.inverse();
//std::cout << "X_ " << X_[0] << std::endl;
X_ = X_ + K * y;
long x_size = X_.size();
Eigen::MatrixXd I = Eigen::MatrixXd::Identity(x_size, x_size);
P_ = (I - K*H_)*P_;
}
4. 结果显示

同时画出测量和卡尔曼滤波后的结果,如图7所示,图中绿色的点为lidar的原始检测结果,蓝色的线为卡尔曼滤波后输出的track结果,目标物在做「8字运动」。从图中可以看出, tracker轨迹的趋势与lidar检测的结果基本一致,且经过卡尔曼滤波后,蓝色track的轨迹相对绿色的原始检测点更加平滑,体现出了卡尔曼滤波器的作用。
/*
draw
.
py
*/
import
matplotlib.pyplot
as
plt
import
numpy
as
np
x
=
[]
y
=
[]
detectX
=
[]
detectY
=
[]
# 存放结果的路径
with
open
(
"jieguo/test7.txt"
,
"r"
)
as
f
:
for
line
in
f
.
readlines
():
line
=
line
.
strip
(
'
\n
'
)
data
=
line
.
split
(
' '
)
count
=
0
for
s
in
data
:
if
s
!=
'X:'
and
s
!=
''
and
count
<
2
:
if
(
count
==
0
):
x
.
append
(
float
(
s
))
count
+=
1
continue
if
(
count
==
1
):
y
.
append
(
float
(
s
))
count
+=
1
# 存放原始检测结果的路径
with
open
(
"./obj_pose-laser-radar-synthetic-input.txt"
,
"r"
)
as
fileIn
:
count
=
0
for
line
in
fileIn
.
readlines
():
line
=
line
.
strip
(
'n'
)
data
=
line
.
split
(
'
\t
'
)
if
(
data
[
0
]
==
'L'
and
count
<=
9
):
detectX
.
append
(
float
(
data
[
1
]))
detectY
.
append
(
float
(
data
[
2
]))
#count += 1
print
(
detectX
)
print
(
detectY
)
plt
.
figure
(
figsize
=
(
6
,
3
))
plt
.
plot
(
x
,
y
,
'b'
)
plt
.
scatter
(
detectX
,
detectY
,
s
=
10
,
color
=
"g"
)
plt
.
show
(
)
参数讨论
(1) 调整P矩阵初值
将P由原来的 \left(\begin{array}{ccc} 1&0&0&0\\ 0&1&0&0\\ 0&0&1000&0\\ 0&0&0&1000\end{array}\right) 调整为 \left(\begin{array}{ccc} 1000&0&0&0\\ 0&1000&0&0\\ 0&0&1000&0\\ 0&0&0&1000\end{array}\right)

从图8中可以看出,调整P的初值对结果无影响。因为从理论上讲,P的初值只代表了刚开始时我们对目标物状态量的一个置信度,将x和y的置信度从1调整为1000, 说明我们对刚开始时目标物的位置不太确定,是随便估计的。但是随着测量结果的迭代,目标物状态的置信度会逐渐回归,而不受初值的影响;
(2) 调整R矩阵
将R矩阵由 \left(\begin{array}{ccc} 2&0\\ 0&2\\ \end{array}\right) 调整为 \left(\begin{array}{ccc} 0.02&0\\ 0&0.02\\ \end{array}\right)

从图9可以看出,调整R矩阵后,卡尔曼滤波输出的结果更加贴近传感器的检测结果,但平滑度降低。从理论上分析,R矩阵表征的是传感器测量的误差,当我们把R矩阵对角线元素由2调整为0.02时,其物理含义为,原来传感器的测量误差为2,调整后的传感器测量误差为0.02,测量误差减小了100倍,且误差只有0.02,表示我们十分相信传感器的结果,这样势必会导致卡尔曼滤波的结果更加贴近传感器原始的检测结果,理论与实践表象一致。
(3) 调整Q矩阵
Q矩阵中 noise_ax = 3; noise_ay = 3 调整为noise_ax = 0.03; noise_ay = 0.03
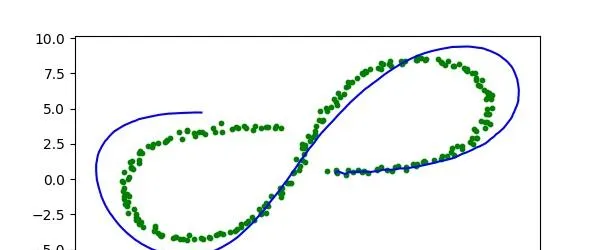
从图10中可以看出, tracker的估计更加平滑,但是偏离原始传感器检测结果也更远了。Q矩阵表征了偏离运动模型的噪声的大小,当我们将噪声 noise_ax 和noise_ay 从3变为0.03时,实际上是降低了过程噪声,也就是更加相信我们建立的运动模型(F),也就是相对不太相信传感器检测的结果,这就会造成我们偏离原始检测结果。
以上是本文的全部内容:。
代码及数据链接: https:// pan.baidu.com/s/1dwYxjJ HLoK_Ox5KcRHgY5A 提取码: 7h8r
参考
- ^ 数据集来源: http://www.udacity.com
- ^ Q矩阵的推导方式举例 https://mp.weixin.qq.com/s?__biz=MzI1ODYwOTkzNg==&mid=2247508342&idx=2&sn=a701c65ed5b5f92f6342ec33b2ea3c8c&chksm=ea076709dd70ee1f3fe318ee446649173a33f7dd2e28f9804c39e343f20de5bccd82f453fb25&mpshare=1&scene=1&srcid=0220DoPOR0CZDTKVgvobFDRL&sharer_sharetime=1613783463771&sharer_shareid=def5d1aee922d88fa623ca1b2829e1b1&exportkey=AzSVmNVaVNURmrtGbLbGqls=&pass_ticket=iyHntop8n5h0fEKwEtMpyGNmmY8acj76sGVADlrFzXB+xvPwOQXHalukuVgreDj&wx_header=0#rd











