这个问题必须加一个前置条件,即自底向上 (bottom-up) 的建堆方式,也就是 Floyd 建堆算法。因为方向相反、自顶向下 (top-down) 的建堆方式的时间复杂度为 O(n·logn).
因此问题应该是 Floyd 建堆算法的时间复杂度为什么是 O(n) ?
关键词:等差-等比数列求和,错位相减法,等比数列求和公式。
首先设置研究这个问题的前置条件:
假设目标堆是一个满堆,即第 k 层节点数为 2ᵏ。输入数组规模为 n, 堆的高度为 h, 那么 n 与 h 之间满足 n=2ʰ⁺¹ - 1 ,可化为 h=log₂(n+1) - 1 。 (层数 k 和高度 h 均从 0 开始 ,即只有根节点的堆高度为0,空堆高度为 -1)。
建堆过程中每个节点需要一次下滤操作,交换的次数等于该节点到叶节点的深度。那么每一层中所有节点的交换次数为节点个数乘以叶节点到该节点的深度(如第一层的交换次数为 2⁰ · h,第二层的交换次数为 2¹ · (h-1),如此类推)。从堆顶到最后一层的交换次数 Sn 进行求和:
Sn = 2⁰ · h + 2¹ · (h - 1) + 2² · (h - 2) + ...... + 2ʰ⁻² · 2 + 2ʰ⁻¹ · 1 + 2ʰ · 0
把首尾两个元素简化,记为①式:
①: Sn = h + 2¹ · (h - 1) + 2² · (h - 2) + ...... + 2ʰ⁻² · 2 + 2ʰ⁻¹
对①等于号左右两边乘以2,记为②式:
②: 2Sn = 2¹ · h + 2² · (h - 1) + 2³ · (h - 2) + ...... + 2ʰ⁻¹ · 2 + 2ʰ
那么用②式减去①式,其中②式的操作数右移一位使指数相同的部分对齐(即错位相减法):
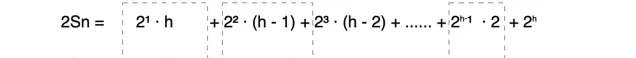
化简可得③式:
③ = Sn = -h + 2¹ + 2² + 2³ + ...... + 2ʰ⁻¹ + 2ʰ
对指数部分使用等比数列求和公式:Sn=\frac{a_{1}\times\left( 1-q^{n} \right)}{1-q}
在这个等比数列中,a1=2, q=2,则③式为:
Sn=-h+\left( \frac{2\times\left( 1-2^{h} \right)}{\left( 1 - 2 \right)} \right)
化简为④式:
④ = Sn = 2ʰ⁺¹ - (h + 2)
在前置条件中已得到堆的节点数 n 与高度 h 满足条件 n=2ʰ⁺¹ - 1(即 2ʰ⁺¹=n+1) 和 h=log₂(n+1) - 1,分别代入④式中的 2ʰ⁺¹ 和 h,因此:
Sn=\left( n + 1 \right) - \left( log_{2}\left( n+1 \right) - 1 + 2 \right)
化简后为:
Sn = n - log₂(n + 1)
因此最终可得渐进复杂度为 O(n).
(补充一下个人看法)
由于对数的部分 log₂(n + 1) 是一个正数,所以 n - log₂(n + 1) < n ,因此最终结果不仅从渐进角度而言为 O(n), 从常系数的角度来说,是比 O(1n) 更优。即 O(an), 0 < a < 1;











