学物理的强答一波。
我目前见过最神的数学知识,或者是一个工具,要数李代数里的Dynkin diagram了,它可以直接把一个本科高年级的数学问题转化为一个小学生都会的问题,虽然小学生不会理解它背后的数学意义,但是会了这个工具,还真能把大学生的题做出来。
数学里直接暴力证明两个李代数同构,或者证明谁是谁的subalgebra,往往是个比较复杂的工程,尤其是当研究的代数变得复杂的时候。但是所有的semi-simple Lie algebras(准确一点说是它们的complexfication),可以根据它们的roots被归类成下面这几种Dynkin diagrams。

记得初学李代数的第一道作业题,老师让我们证 SU(4) 和 SO(6) 的李代数同构,那时候还尝试用6维的 \gamma 矩阵去同时构造这两个代数generator间的对易关系,算了几页纸才解决,结果学了Dynkin diagram之后,知道 SU(4) 李代数对应上面 A_{3} 的图, SO(6) 李代数对应 D_{3} 的图,它们俩都是三个黄点连起来,长得一样,所以就同构了,一秒钟,用眼睛看,就能得到结论。复杂的数学题变成了一个认图的问题,知道了规则,真的是小学生都会了。
除此之外,引入extended Dynkin diagram的概念,还可以用来证明一个李群是另一个李群的子群。
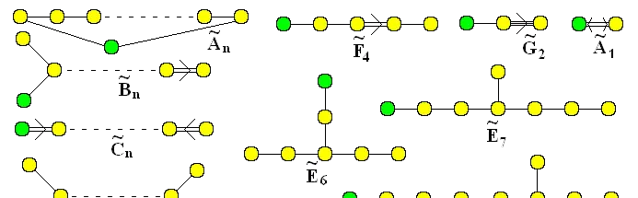
把extended Dynkin diagram拿掉一个点,剩下的图所对应的李代数就是之前extended的图对应的李代数的subalgebra。比如从 \widetilde{E}_{8} 里拿掉最中间那个黄点,剩下两个一模一样的四个黄点串联,每个四个黄点相当于一个 A_{4} ,就能证明 SU(5)\times SU(5)\subset E_{8} 。也是一秒钟就能做出来的问题,但如果从基本定义暴力算,那花的时间不知道有多少倍。
当然Dynkin diagram是个比较基础的概念,学过李代数的人都知道,作为数学知识本身没有鹤立鸡群的地方。而且之所以用它证明同构或者子群这么快,是因为复杂的步骤在构造这些图的时候已经有人帮你做过了。它让我「惊呆」的点在于,应用起来是真的方便。我没见过用其简化问题前后,问题难度差距如此之大的数学工具。学的时候我就感叹这简直绝了。










