几何的观点 :如果把方阵视为线性变换,则其行列式的绝对值表示该线性变换造成的体积元的变化系数,行列式的符号反映了基底的定向变化。
比如,行列式可表示平行四边形或平行六面体的有向面积/体积,因为平行四边形和平行六面体实际上分别是平面和空间中另一组基底构成的面积元/体积元。
比如,行列式为零,表示线性变换是奇异的,即把原空间的体积元变成零了,一一对应就不存在了
又比如,导数实际上是线性变换 (微分实际上是两个切空间之间的线性变换,比如一元函数实际上是一维实轴到一维切线之间的线性变换,得到的斜率只是一个数,但实际上是1x1矩阵),于是积分变换中的Jacob行列式实际上是此线性变换的行列式,它的绝对值是体积元dxdydz的系数。
代数的观点 : 行列式无非是方阵的一个函数,但它是一种反对称多重线性型,比如f(\alpha x_1,x_2,x_3)=\alpha f(x_1,x_2,x_3) ,-f(x_1,x_2,x_3)=f(x_2,x_1,x_3) ,多重线性性体现在每一行或每一列的线性性质,反对称体现在两行或两列交换后变负。同为行和列的反对称多重线性型,行列式的计算方式也就确定了。
这两种观点都不允许非方阵的行列式的定义。
===============================================================
补充一下,问一个数学工具的本质,窃以为并不妥当,有一点追求终极真理的感觉,在哲学上并不能自洽。不如先看一下它的历史,然后再观察一下它有哪些深刻的应用。
历史上,行列式先于矩阵,用于求解线性方程。行列式是否为零可用来判定一个线性方程是否有解,然后Cramer规则直接用行列式给出线性方程的解。随后,行列式才被视为一个矩阵的函数。
数学上的两条重要的主线:解方程和微积分在线性代数上统一起来了,因为微分实际上就是一种线性逼近。因而,矩阵和行列式在这其中起到的作用就非常深刻了。而行列式作为一个函数具有的反对称线性性在抽象代数是一个非常重要的概念。
所以说,行列式只不过是数学家在解决实际问题时发明的一个很好用的工具,恰好它又可以在许多的应用中发挥作用。
================================================================
再补充一下,几个常用的行列式应用
-
积分变换与Jacob行列式 (体积元都为正,所以取行列式的绝对值)
(v_1,\cdots,v_n)=\varphi(u_1,\cdots,u_n) \Rightarrow dv_1 \cdots dv_n = |\det(\operatorname{D}\varphi)(u_1, \ldots, u_n)| \, du_1 \cdots du_n
-
Cramer规则
Ax=b 的解为x_i=\frac{|A_i|}{|A|} ,其中A_i 为将A 的第i 列换成b
-
平行四边形面积,从原点出发的两个矢量\boldsymbol{v}_1,\boldsymbol{v}_2
构成的平行四边形的有向面积为
\operatorname{det}(\boldsymbol{v}_1,\boldsymbol{v}_2)=\left|\begin{matrix}v_{11},v_{21}\\v_{12},v_{22}\end{matrix}\right|
-
平行六面体体积

-
叉乘的另一种定义
(x_1,y_1,z_1)^T\times(x_2,y_2,z_2)^T=\left|\begin{matrix}i&j&k\\x_1&y_1&z_1\\x_2&y_2&z_2\end{matrix}\right|
-
判断共面
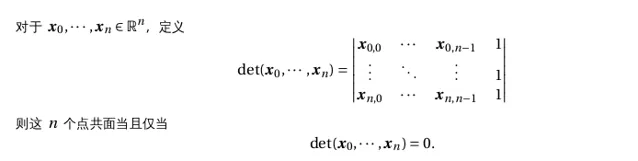
-
判断共圆












