在考虑等价关系、相容关系、偏序关系之前,我们需要对关系的关键性质做一个感性、直观的理解。离散数学里面的这些形式化的定义,和生活更是紧密相关啦,在计算机领域会大量用于问题建模。
注意,我们讨论的关系,都是在某个集合(比如A)上的关系,即二元组的两项都属于A。下面用R指示关系,用A指示关系所在集合。
关系的五种性质
自反性与反自反性:是否每个元素与其本身构成关系?还是每个元素与自己都没有关系?
对称性与反对称性:关系是否是完全双向的?是否是绝对单向的?在后面,配合传递性,对称性自然引出了等价关系,反对称性引出了偏序关系。
传递性:传递性意味着关系的扁平化,在「距离」上的invariance。
- 从关系图的视角看,从任何一个点走两步都不会抵达新的位置,也意味着,任何能到达的位置都可以一步到达(扁平化的意味);
- 体现在关系矩阵上,它(在逻辑上)呈现一种上/下三角的状态,比如a->b->c的关系矩阵——对于一个传递性的关系,其中任意一个「传递链条」,都呈现上/下三角的样态【注意,是可以通过对完整的关系矩阵进行初等变换后,可以使这一个链条所对应部分成为上/下三角的样态】。

传递性由合成运算而来。我们也一起重新回顾一下。
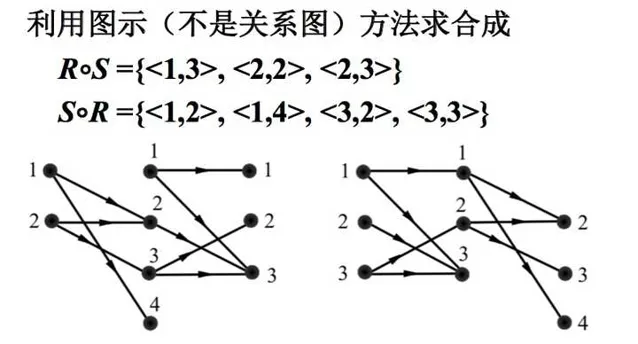
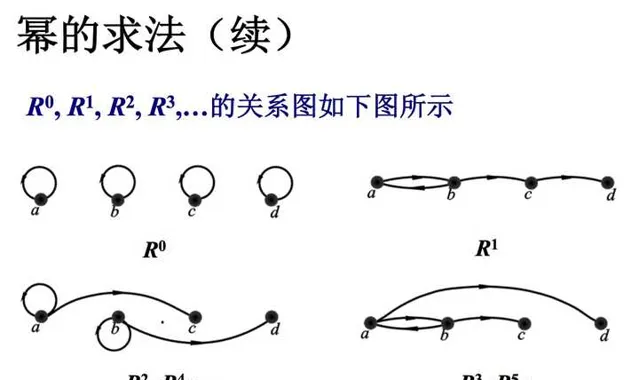
从哈斯图中看传递性的意义:我们不再关注任意两元素中间有多少个结点。
对五种性质理解的强化
- 五种性质的充要条件是什么?

2. 如何判别这五种性质?
从关系图、关系矩阵,配合定义,以及生活中(或者数学中)的例子,在此处可以对五种性质做一个直观的感受。比如传递性:因果链是传递的,事件A是事件B的一个前提,事件B是事件C的前提,那么A也是C的前提——所以若不做无限后推,那我们就需要一个第一因 :-)。这里需要大家建立思考。
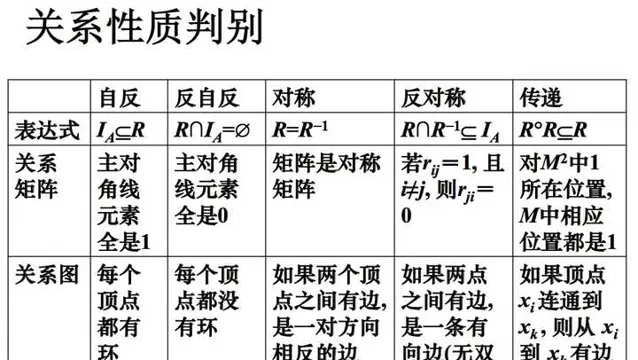
3. 如何证明某个关系符合性质?

4. 运算与性质的关系——运算维持相应性质吗?为什么?此处可以进一步深化直观理解。
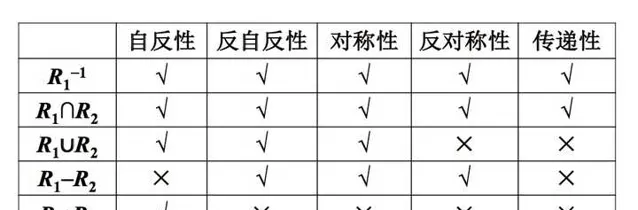
我对不再保持的性质做简单的自己的解读。
集合的差不再保持自反性:对角线都被剪掉了嘛。
集合的合成不再保持反自反性:扁平化后,自己就算是指向自己了。
集合的合成不再保持对称性:对接处可能未连接上,如{<1,3><3,1>}与{<2,3>,<3,2>},是二元组的顺序带来的。
集合的并集不再保持反对称性:可能两者直接互补了嘛。交集为何可以?因为一定会更小。
集合的合成不再保持反对称性:看传递矩阵,反自反性的单向性是一个非常弱的约束,R2可以对R1做任意的调整,让某个元素指回自己。【这里有些词不达意。可以自己画画计算集合合成的那张图】
到了传递性:为何交运算保持?三角与三角的交集还是三角;并运算不保持?三角与三角的并集会缺一个角,连通性仅部分地被扩张了;合成也不行?和并运算类似嘛。
5. 闭包的构造:为何传递闭包要比对称闭包后算?: -)对称闭包让所有关系都变成了双向,比如 a->b->c与d->b->c,a与d是没关系的,所有关系右多了个反向,他俩就应该有关系了。
等价关系、相容关系、偏序关系
- 等价关系:自反 + 对称 + 传递
若说传递性的扁平化还没有消除关系的方向性,那么它与对称性的配合就彻底的让关系变成了零维的,完全失去了阶级性(偏序还保持这一点)。之前说,传递性可以理解为上/下三角,那么配合对称(以及比较trivial的自反性,它就是对角线),那么就是个正方形了。正方形意味着,其内部关系的完整性,以及与其他元素的隔离性。而对于等价关系,它的关系矩阵一定可以转换为只在其对角线围绕着一串正方形的形式。
在等价关系中,一个等价类不分阶级、不同等价类不可比较。
应该很好理解了。商集,就是所有等价类的集合;划分,就是所有等价类摆在一起;块数,就是划分的秩。
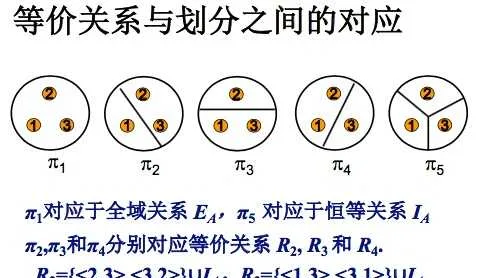
我们如何求一个划分呢?根据问题中的等价条件,抽象出等价的形式定义就好啦。
总结:等价关系是一种条件极其强大(简单)的关系,它完全消解的关系运算中的invariant,完全扁平化。
2. 相容关系:自反 + 对称
朋友的朋友不一定是朋友,但也很有可能是朋友,朋友关系就是相容关系的一个很好例子。相容关系中,最主要的就是「对称性」,也就是双向性,是相容的意味。相容关系消解了方向性。
一个朋友圈,就是一个相容类(主要是「最大相容类」概念):这个圈子内的人彼此都是朋友,这是类似等价类的概念。但一个人可以处于多个圈子内,这是与等价类不同处。
我们想象一个N个人的完整的社交圈:那就是要看这些人的朋友关系的 完全覆盖 ,即所有最大相容类的集合。再申,一个人可以出现在多个最大相容类中,这是与等价关系的差异。
3. 偏序关系:自反 + 反对称 + 传递
还用三角的比喻,偏序关系就是带对角线的三角,且不允许出现边长大于1的正方形。

两个元素可比,意味着在同一个三角形上(还是逻辑上的三角形,可能需要堆关系矩阵经过变换得到)。全序,则是一个巨大的三角形。
覆盖关系,用于找到在偏序集上最紧凑的(相邻的)两个元素,用于后面画哈斯图。由于偏序关系有方向,还是保持着某种「距离」的含义,但它对这个关系本身无任何内涵上的联系,只是用来画图而已。
偏序集:集合 + 偏序运算。
哈斯图:就是很像树的图,「父子」的关系是覆盖。哈斯图中可能有许多树。每棵树可以有许多树根【极小元】。每棵树可以倒过来,看起来还是一棵树。上下界、上下确界,存在性也就很显然啦。无限,也就可能无界,正如因果链,有没有第一因呢!对于无限集合,确界,也可能在关系的定义域之外,类似开区间与其边界的关系。
一点点拓展:链、反链、良序它们有一点点性质:
可以发现拓扑排序与链的关系。
良序:任意非空子集都存在最小元的偏序集。
这三个概念,也可以加深对于关系的理解~ 不过,我们会发现我们的思维是越来越抽象的,自底向上,似乎已经远远离开了关系的定义了: -)
先这些吧。











