如何「破译」清朝的微积分课本？

前两天看到了网上流传的清朝的微积分课本中的几页，其中的所有数学表达式都是用中文书写的。虽然整个过程不忍直视，但还是感觉蛮有趣的。于是我打算写篇文章翻译一下这几页。 ^{[1] [2]}

下面我们先来看到第一页：

请您上眼。乍一看大家肯定觉得：这都啥啊？这样的公式好丑，怎么能记得住呢？而且这里面居然还有完全不认识的字？比如一个双人旁一个天念啥？

下面我就要使用魔法将这些丑丑的公式翻译成能看的懂的形式了。

在翻译之前，我们要明确的一个 大原则 是：在清朝， 「分数」的「分子」是分母，「分母」是分子 。也就是说， 如果看到「分数」，则我们取它的倒数就可以得到现代意义下的分数 。

首先映入眼帘的是：

戍=天^{天}\tag{1}

这明显是一个函数，它翻译成英语就是：

y=x^x.\tag{2}

啊，看着舒服多啦～这道例题提到了「...求其微分之式，则可依blabla...」。害，无所谓依啥了，我们自己就可以搞定。求 (2) 这个函数的微分函数比较容易的。首先将 x^x 改写一下：

x^x=\exp\left(x\cdot\ln\left(x\right)\right).\tag{3}

进而成立：

\frac{\mathrm{d}}{\mathrm{d}x}\left( x^x \right)=\frac{\mathrm{d}}{\mathrm{d}x}\left(\exp\left(x\cdot\ln\left(x\right)\right)\right)=\exp\left(x\cdot\ln\left(x\right)\right)\cdot\left(\ln\left(x\right)+1\right)=x^x\cdot\left(\ln\left(x\right)+1\right).\tag{4}

即：

{\mathrm{d}}y=x^x\cdot\left(\ln\left(x\right)+1\right)\,{\mathrm{d}x}.\tag{5}

与：

做比较可以得到以下破译密码：

第一个公式的破译工作就完成啦～很顺利是不是！但是，下一个公式就很难破译了。没错，就是它：

这个公式，堪称我破译工作中最可(**)爱(**)的一个。先不管天啊，地啊啥的。从刚才的破译密码中我们得知的信息是 双人旁 =\mathrm{d} ，于是问题就出现了这里面有 \mathrm{d}戍 ， \mathrm{d}地 以及 \mathrm{d}天 。咦？这么快就跳到全微分啦？但仔细不看不对啊，这跟全微分完全不沾边啊。于是我推测，这不是全微分，而是刚才例题的推广，因为我在下面的结果中看到了天的地次方： 天^{地} ：

此处的天和地不能再理解为 x 和 y 了，而是应该理解为 f\left( x \right) 与 g\left( x \right) ，说白了，就是对函数：

y=f^{g\left( x \right)}\left( x \right).\tag{6}

求导（天^{地} 这个表达简直了。。。哈哈哈哈哈哈哈）。

像破译第一个公式一样，这里我们如法炮制即可。首先将 f^{g\left( x \right)}\left( x \right) 改写一下：

f^{g\left( x \right)}\left( x \right)=\exp\left(g\left( x \right)\cdot\ln\left(f\left( x \right)\right)\right).\tag{7}

进而成立：

\begin{array}{ll} \display style{\frac{\mathrm{d}}{\mathrm{d}x}\left(f^{g\left( x \right)}\left( x \right)\right)} & \display style{=\frac{\mathrm{d}}{\mathrm{d}x}\left(\exp\left(g\left( x \right)\cdot\ln\left(f\left( x \right)\right)\right)\right)}\\ & \display style{=\exp\left(g\left( x \right)\cdot\ln\left(f\left( x \right)\right)\right)\cdot\left(g'\left( x \right)\cdot\ln\left(f\left( x \right)\right)+\frac{g\left( x \right)}{f\left( x \right)}\cdot f'\left( x \right)\right)}\\ & \display style{=f^{g\left( x \right)}\left( x \right)\cdot\left(g'\left( x \right)\cdot\ln\left(f\left( x \right)\right)+\frac{g\left( x \right)}{f\left( x \right)}\cdot f'\left( x \right)\right).} \end{array}\tag{8}

即：

{\mathrm{d}}y=f^{g\left( x \right)}\left( x \right)\cdot\left(g'\left( x \right)\cdot\ln\left(f\left( x \right)\right)+\frac{g\left( x \right)}{f\left( x \right)}\cdot f'\left( x \right)\right)\,{\mathrm{d}x}.\tag{9}

将式 (9) 进一步化简可得：

{\mathrm{d}}y=f^{g\left( x \right)}\left( x \right)\cdot\left(\ln\left(f\left( x \right)\right)\,{\mathrm{d}g}+\frac{g\left( x \right)}{f\left( x \right)}\,{\mathrm{d}f}\right).\tag{10}

现在我们将 y=f^{g\left( x \right)}\left( x \right) 除到左边之后与之前所提到的 大原则 一起可得：

\frac{\mathrm{d}y}{y}=\frac{g\,{\mathrm{d}f}}{f}+\ln\left(f\right)\,{\mathrm{d}g}.\tag{11}

将式 (11) 与：

做比较可得：

这样第一页我们就完全破译啦！下面开始第二页的破译～

这一页的破译工作会异常轻松。首先我们看到了「积分」这个字眼，并且他说「啥啥（就是那个怪怪的公式），要必为简式」才可求其积分。所以我们不妨先来看看：

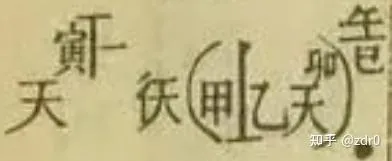
这是个啥？

由之前所总结的破译密码可知，天一定代表一个「变量」。而且我们还知道长得像垂直符号的那个符号等价于加法，因此我们推测：

而甲，乙，丙...啥的自然表示的就是常数 a,\,b,\,c... 等等。至于寅卯午巳这些字，如果你愿意，可以定义为 \alpha,\,\beta,\,\gamma,\,\delta 等等，它们也都表示常数。因此，我们可以将其破译为（指数上注意 大原则 ）：

x^{\alpha-1}\,\mathrm{d}x\left(a+b\cdot x^{\beta}\right)^{\frac{\delta}{\gamma}}.\tag{12}

同理，我们可以将：

破译为（指数上注意 大原则 ）：

x^{\alpha+\frac{\beta\cdot\delta}{\gamma}-1}\,\mathrm{d}x\left(a\cdot x^{-\beta}+b\right)^{\frac{\delta}{\gamma}}.\tag{13}

聪明的你一定发现了：

表达的就是不定积分的分部积分法：

\int u\,\mathrm{d}v=u\cdot v-\int v\,\mathrm{d}u.\tag{14}

破译密码为：

最后是第三页：

有了之前两页的经验，相信这一页大家一定得心应手啦。在这一页中，所有的汉字数字与阿拉伯数字的含义是一致的。而天，地，人（这应该是人吧）表示的都是变量。因此我们可以设：

天:=y,\quad地:=z ,\quad 人:=x.\tag{15}

因此：

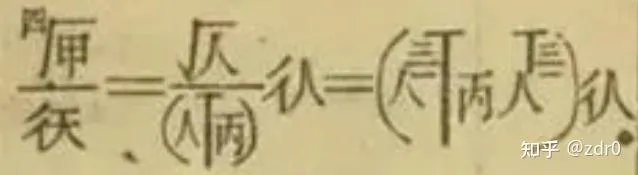
表示（注意 大原则 ）：

\frac{\mathrm{d}y}{\sqrt[4]{a}}=\frac{x-c}{\sqrt{x}}\,\mathrm{d}x=\left( x^{\frac{1}{2}}-c\cdot x^{-\frac{1}{2}} \right)\,\mathrm{d}x.\tag{16}

而：

表示（注意 大原则 ）：

\frac{y}{\sqrt[4]{a}}=\frac{2}{3}\cdot x^{\frac{3}{2}}-2\cdot c\cdot x^{\frac{1}{2}}+C.\tag{17}

显然，式 (17) 是式 (16) 的一个原函数。而丙上面加一个点表示的是积分常数 C ，与普通的丙表示的 c 是不一样的（二丙，看起来像麻将）。

现在让我们看到最右边的：

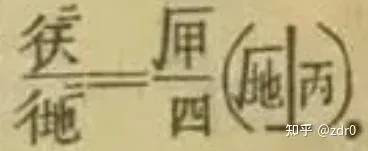
这表示的显然是（注意 大原则 ）：

\left(\frac{\mathrm{d}z}{\mathrm{d}y}\right)^2=\frac{4}{\sqrt{a}}\cdot\left(\sqrt z+c\right).\tag{18}

我一度认为左边是二阶导数。。。后来一想不对，如果是二阶导数的话「分母」上的二应该在双人旁后面。因此：

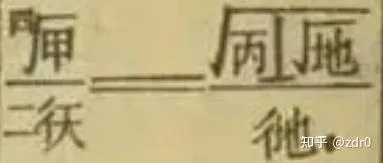
表示的是（注意 大原则 ）：

\frac{2\cdot \mathrm{d}y}{\sqrt[4]{a}}=\frac{\mathrm{d}z}{\sqrt{c+\sqrt{z}}}.\tag{19}

然后后面说可以将 c+\sqrt{z}:=x ，进而：

表示的就是（注意 大原则 ）：

\frac{y}{\sqrt[4]{a}}=\frac{2}{3}\cdot \left( c+\sqrt{z} \right)^{\frac{3}{2}}-2\cdot c\cdot \left( c+\sqrt{z} \right)^{\frac{1}{2}}+C=\frac{2}{3}\cdot \left(\sqrt{z}-2c \right)\cdot \left( c+\sqrt{z} \right)^{\frac{1}{2}}+C.\tag{20}

参考

1. ^ https://www.bilibili.com/video/BV1pU4y1T7bt?from=search&seid=6680661053013392242&spm_id_from=333.337.0.0
2. ^https://www.youtube.com/watch?v=BA3f_-J_Gmc&t=408s