省流版本:在100000次的模拟中,100,78,95名列前三;分别存活了1097,1093,1089次,最大存活率在1.1%左右;27,18和12最危险,都只存活了868,903和909次。
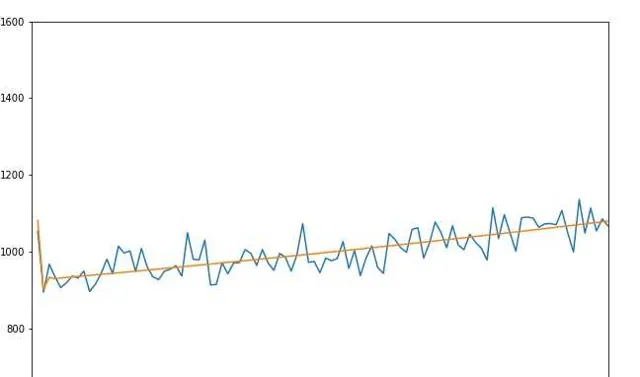
如下图所示,其中蓝色线段为100000次的模拟数据,黄色线段为 @张雄骐 大佬的解析解的结果,我们可以看出二者是十分吻合的 [1] 。解析解指出1号将具有最大的生存率,实际上如果我们把1号视作最后接受枪击的101号的话,我们也能自然地看出『 序号越大后生存机率越大 』的特点。
经典的约瑟夫问题的变形,引入了左轮赌局这个随机变量。我们这里假设每次开枪意味着有六分之一的概率死亡,那么我们就可以先模拟一下。
首先,我们先生成一个标准的 循环链表 。

class Node(object):
def __init__(self, value):
self.value = value
self.next = None
def create_linkList(n):
head = Node(1)
pre = head
for i in range(2, n+1):
newNode = Node(i)
pre.next= newNode
pre = newNode
pre.next = head
return head
如果开枪成功,我们就将当前Node从 循环链表 中移出,直到整个循环链表中只剩下一个Node时游戏结束。
def test():
head = create_linkList(100)
pre = None
cur = head
while cur.next != cur:
pre = cur
cur = cur.next
# 引入判定条件
if randint(1,6) == 1:
pre.next = cur.next
cur.next = None
cur = pre.next
return cur.value
之后我们再模拟10000次,再排序就出现结果了。

然后是上述模拟程序的可能的误差来源。
首先是用于生成随机数
randint
函数,此函数的随机性由Mersenne Twister算法保证,理论上的随机数周期为 2^{19937}-1
,以目前的循环次数来看,还是
不需要考虑因随机数循环导致的取样偏差的
。
评论区中给出了另外一种理解题意的方式,即『 若枪未发射,则继续传递,所以下一发射出的概率应该增加 』。从个人角度来说,我认为这两种情况在统计结果上应该是等价的。就类似与开奖先后的顺序实际上不会影响获奖概率的。
update
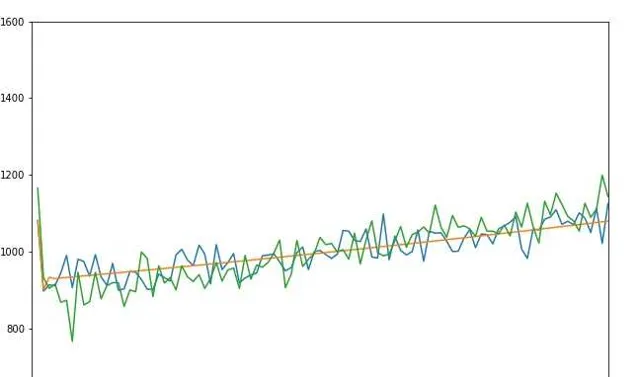
上述解法给出的是『每位都有六分之一的概率死亡』的模拟,这一点和题目中所谓的『传递手枪』的说明并不完全相同。以下给出『 传递手枪 』的解法:
def test_same_gun(n):
head = create_linkList(n)
pre = None
cur = head
bullet_pos = randint(1,6)
while cur.next != cur:
# 传递手枪
for _ in range(bullet_pos):
pre = cur
cur = cur.next
bullet_pos = randint(1,6)
pre.next = cur.next
cur.next = None
cur = pre.next
return cur.value
可以料想,『传递手枪』实际上相当于给所有人分组了,比如2-7号,其中必定至少会有一人被射击。
参考
- ^https://www.zhihu.com/question/8225556361/answer/67650588974










