直接上结论第一个人存活概率就是最高的。
题目是经典约瑟夫环问题的概率版本。
对于概率游戏直接暴力模拟就好,如果没有好的结果,那一定是模拟次数太少了,增加模拟次数即可。
另外,类似约瑟夫环的问题,基本可以用递推公式求解。
两种理解方式
不过看了一下评论区,看起来对开枪的概率有两种理解。
1) 死亡概率不是定值
只有装填子弹的的那个人,才会旋转手枪旋转轮。也就是刚填子弹时,开枪是1/6死亡率,如果没有射出子弹,下一个人开枪,就会有1/5的概率射出子弹,然后1/4, 1/3,1/2, 1/1。
2) 死亡概率是定值
每次开枪都是1/6死亡率,也就是每个人在射击前,都随机旋转一下手枪旋转轮。
当然不管是哪种理解方式,都是第1个存活概率最高。
死亡概率不是定值时理论计算
采用递推方式求解这个问题。
状态定义
记 P(n, m, k) 表示 当游戏有 n 个人且第1个人开枪射出子弹的概率为 \frac{1}{k} 时,第 m 个人的最终存活概率。
递推关系
于是可以找它的递推公式,并不会复杂,按第一个人开枪后是否射出子弹分两种情况就好。
1) 如果第一个人打出子弹,第2个人直接死亡,那么人数就变为 n-1 , 而且枪会到第3个人手中并且概率会重置为 \frac{1}{6} 。于是相当于从第3个人开始对每个人重新标号继续进行游戏,所以原来的第1个人变为 n-1 人,第 m 个人变为 m-2 人。
2)如果第一个人没打出子弹,那么枪到2号手中,而且2号开枪射出子弹的概率增加为 \frac{1}{k - 1} 。于是相当于从第2个人开始对每个人重新标号继续进行游戏,所以原来的第1个人变为第 n 人,第 m 个人变为 m-1 人。
根据两种情况得到如下递推公式:
P(n, 1, k) = \frac{1}{k}P(n - 1, n - 1, 6) + (1 - \frac{1}{k})P(n, n, k - 1)\\ P(n, 2, k) = (1 - \frac{1}{k})P(n, 1, k - 1)\\ P(n, 3, k) = \frac{1}{k}P(n - 1, 1, 6) + (1 - \frac{1}{k})P(n, 2, k - 1)\\ \vdots\\ P(n, m, k) = \frac{1}{k}P(n - 1, m - 2, 6) + (1 - \frac{1}{k})P(n, m - 1, k - 1)\\ \vdots\\ P(n, n, k) = \frac{1}{k}P(n - 1, n - 2, 6) + (1 - \frac{1}{k})P(n, n - 1, k - 1)
其实就2号的递推比较特殊,他可能第一枪就死掉。
边界条件
边界条件 P(1, 1, k) = 1 这是显然的,只有一个人时,他总不会自杀吧。
目标
求解的目标是 P(n, i, 6) 对每个 1\leq i \leq n 。
然后实现就简单记忆化搜索了,关键代码如下:
from
functools
import
lru_cache
@lru_cache
(
maxsize
=
None
)
def
P
(
n
,
m
,
k
):
if
n
==
1
and
m
==
1
:
return
1.0
if
m
>
n
or
m
<=
0
:
return
0.0
if
m
==
1
:
prob_shoot
=
(
1.0
/
k
)
*
P
(
n
-
1
,
n
-
1
,
6
)
prob_not_shoot
=
(
1.0
-
1.0
/
k
)
*
P
(
n
,
n
,
k
-
1
)
if
k
>
1
else
0.0
return
prob_shoot
+
prob_not_shoot
else
:
prob_shoot
=
(
1.0
/
k
)
*
P
(
n
-
1
,
m
-
2
,
6
)
prob_not_shoot
=
(
1.0
-
1.0
/
k
)
*
P
(
n
,
m
-
1
,
k
-
1
)
if
k
>
1
else
0.0
return
prob_shoot
+
prob_not_shoot
def
compute_probabilities
(
n
,
k
=
6
):
probabilities
=
{}
for
m
in
range
(
1
,
n
+
1
):
probabilities
[
m
]
=
P
(
n
,
m
,
k
)
return
probabilities
具体结果如图1所示,显然第1个人的存活概率最大,不过跟第100个人差别不大。然后比较有意思的就是1到7的存活概率递减,第8个人出现一个小峰值,其余的人存活概率整体趋势上升。
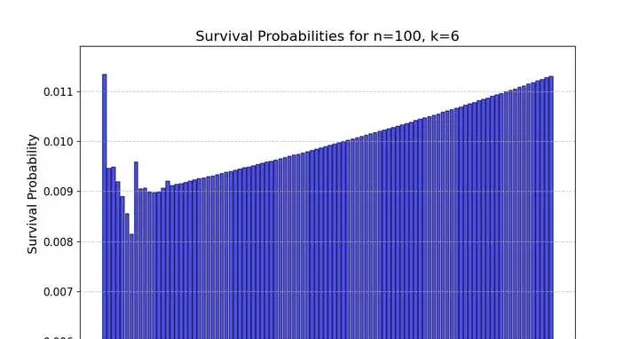
死亡概率不是定值时模拟实验
进行1200万模式实验得到的存活概率和理论值对比结果如图2,会发现几乎重, 因此理论计算没有什么问题。
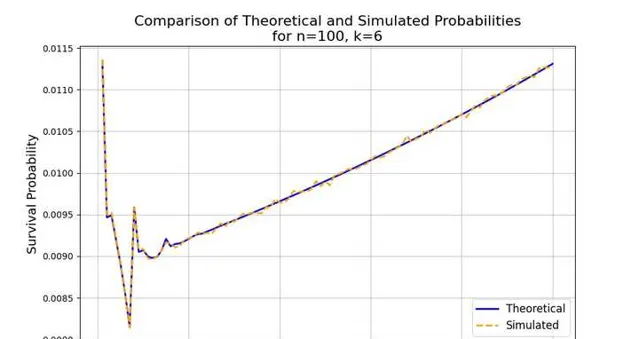
死亡概率不是定值时关键代码
import
random
#死亡概率不是定值
def
simulate_game
(
total_people
,
simulations
):
survival_counts
=
[
0
]
*
total_people
for
i
in
range
(
simulations
):
people
=
list
(
range
(
1
,
total_people
+
1
))
m
=
6
while
len
(
people
)
>
1
:
shooter
=
people
.
pop
(
0
)
if
random
.
randint
(
1
,
m
)
==
1
:
people
.
pop
(
0
)
m
=
6
else
:
m
-=
1
people
.
append
(
shooter
)
if
people
:
survival_counts
[
people
[
0
]
-
1
]
+=
1
return
survival_counts
具体1200万次模拟实验数据如下:
[136348, 113994, 114275, 110564, 107032, 102645, 97681, 115055, 108950, 109036, 107689, 107479, 108013, 108768, 109982, 109844, 109259, 109428, 110391, 110588, 110787, 111405, 111206, 111356, 111210, 111993, 112712, 112253, 113064, 112961, 113604, 114108, 114071, 114312, 114214, 114176, 115046, 115038, 116230, 115751, 115741, 116309, 117383, 117267, 117312, 117263, 117736, 118797, 118066, 118777, 118223, 119616, 119856, 120148, 120555, 120513, 120643, 121042, 121264, 121861, 122409, 122210, 122385, 122925, 123308, 123654, 124216, 125325, 124400, 124942, 125103, 126217, 125747, 126337, 126902, 127028, 127287, 127764, 127839, 128510, 127983, 128841, 129748, 129415, 130387, 130922, 131171, 131123, 131585, 132309, 132694, 132661, 133449, 133725, 134008, 133762, 135055, 135226, 135142, 135396]
死亡概率是定值时模拟实验
这种理解的理论推导和实验评论区都有,这里就不重复推导了,就让计算机做一下模拟实验,做一个补充。进行1200万次模拟实验,得到的结果如图3所示。
存活次数最多的是第1个人129708次,存活次数最少的3个是第2个人108017次
所以结论是
第1个人的存活率是最高的,但是和第100个人,第99个人没有显著的差别。
第2个人的存活旅明显低于其他人,然后就是2到100的存活概率基本在增加。
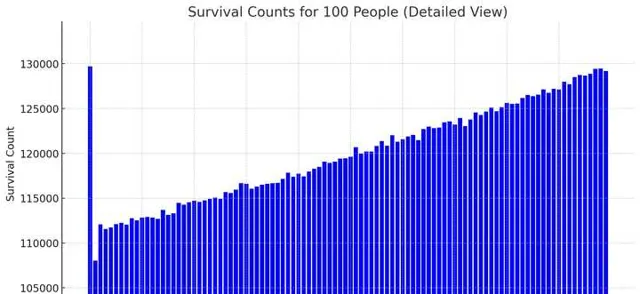
死亡概率是定值的关键代码
import
random
#死亡概率是定值
def
simulate_game
(
total_people
,
simulations
):
survival_counts
=
[
0
]
*
total_people
for
i
in
range
(
simulations
):
people
=
list
(
range
(
1
,
total_people
+
1
))
while
len
(
people
)
>
1
:
shooter
=
people
.
pop
(
0
)
if
random
.
randint
(
1
,
6
)
==
1
:
people
.
pop
(
0
)
people
.
append
(
shooter
)
if
people
:
survival_counts
[
people
[
0
]
-
1
]
+=
1
return
survival_counts
模拟1200万次的实验具体数据如下:
[129708, 108017, 112087, 111569, 111733, 112116, 112248, 112045, 112753, 112508, 112820, 112887, 112844, 112704, 113683, 113131, 113312, 114477, 114278, 114560, 114712, 114587, 114743, 114939, 115076, 114925, 115664, 115581, 115969, 116664, 116613, 116047, 116279, 116505, 116596, 116663, 116693, 117143, 117824, 117382, 117731, 117441, 117980, 118277, 118489, 119072, 118928, 119057, 119404, 119448, 119614, 120669, 119956, 120201, 120205, 120834, 121370, 120872, 122029, 121318, 121566, 121880, 122052, 121477, 122694, 122983, 122823, 122889, 123463, 123570, 123240, 123929, 123049, 123782, 124559, 124293, 124655, 125094, 124705, 125139, 125623, 125533, 125566, 126189, 126513, 126378, 126567, 127151, 126756, 127195, 127134, 127992, 127712, 128501, 128756, 128681, 128875, 129422, 129454, 129180]
最后
如果有幸玩这种游戏,可以先写遗书准备后事。
然后尽量让自己是第一个开枪,如果不能,那就最后一个开枪。










