最喜歡通俗易懂地解釋一個事情。
一、共變異數:
可以通俗的理解為:兩個變量在變化過程中是同方向變化?還是反方向變化?同向或反向程度如何?
你變大,同時我也變大,說明兩個變量是同向變化的,這時共變異數就是正的。
你變大,同時我變小,說明兩個變量是反向變化的,這時共變異數就是負的。
從數值來看,共變異數的數值越大,兩個變量同向程度也就越大。反之亦然。
咱們從公式出發來理解一下:
Cov(X,Y)=E[(X-\mu _{x})(Y-\mu _{y})]
公式簡單轉譯一下是:如果有X,Y兩個變量,每個時刻的「X值與其均值之差」乘以「Y值與其均值之差」得到一個乘積,再對這每時刻的乘積求和並求出均值(其實是求「期望」,但就不引申太多新概念了,簡單認為就是求均值了)。
下面舉個例子來說明吧:
比如有兩個變量X,Y,觀察t1-t7(7個時刻)他們的變化情況。
簡單做了個圖:分別用紅點和綠點表示X、Y,橫軸是時間。可以看到X,Y均圍繞各自的均值運動,並且很明顯是同向變化的。
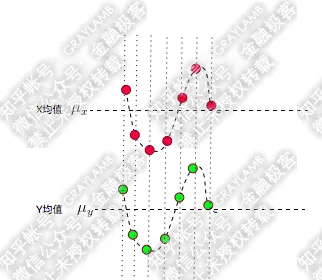
這時,我們發現每一時刻X-\mu _{x} 的值與Y-\mu _{y} 的值的「正負號」一定相同(如下圖:比如t1時刻,他們同為正,t2時刻他們同為負):
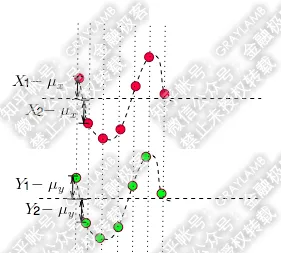
所以,像上圖那樣,當他們同向變化時,X-\mu _{x} 與Y-\mu _{y} 的乘積為正。這樣,當你把t1-t7時刻X-\mu _{x} 與Y-\mu _{y} 的乘積加在一起,求平均後也就是正數了。
如果反向運動呢?
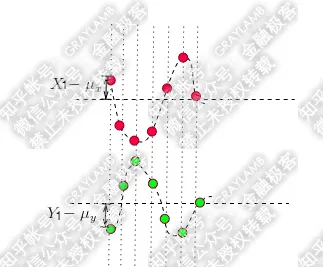
很明顯,X-\mu _{x} 的值與Y-\mu _{y} 的值的「正負號」一定相反,於是X-\mu _{x} 與Y-\mu _{y} 的乘積就是負值了。這樣當你把t1-t7時刻X-\mu _{x} 與Y-\mu _{y} 的乘積加在一起,求平均的時候也就是負數了。
當然上面說的是兩種特殊情況,很多時候X,Y的運動是不規律的,比如:
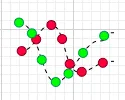
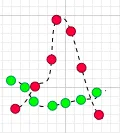
這時,很可能某一時刻X-\mu _{x} 的值與Y-\mu _{y} 的值乘積為正,另外一個時刻X-\mu _{x} 的值與Y-\mu _{y} 的值乘積為負。
將每一時刻X-\mu _{x} 與Y-\mu _{y} 的乘積加在一起,其中的正負項就會抵消掉,最後求平均得出的值就是共變異數,透過共變異數的數值大小,就可以判斷這兩個變量同向或反向的程度了。
所以,t1-t7時刻中,X-\mu _{x} 與Y-\mu _{y} 的乘積為正的越多,說明同向變化的次數越多,也即同向程度越高。反之亦然。
總結一下,如果共變異數為正,說明X,Y同向變化,共變異數越大說明同向程度越高;如果共變異數為負,說明X,Y反向運動,共變異數越小說明反向程度越高。
--------LINE---------
一般的同學看到above the line的內容就ok了。但有一些愛鉆研的同學,可能會進一步提問:
那如果X,Y同向變化,但X大於均值,Y小於均值,那X-\mu _{x} 與Y-\mu _{y} 的乘積為負值啊?這不是矛盾了嗎?
那就繼續往下看……
這種情況是有可能出現的,比如:
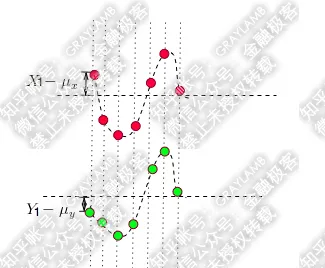
可以看到,t1時刻,X-\mu _{x} 與Y-\mu _{y} 的符號相反,他們的乘積為負值。
但是,總體看,這兩個變量的共變異數仍然是正的,因為你還要計算t2,t3……t7時刻X-\mu _{x} 與Y-\mu _{y} 的乘積,然後再把這7個時刻的乘積求和做均值,才是最後X,Y的共變異數。1個負、6個正,顯然最後共變異數很大可能性是正的。
所以t1時刻X-\mu _{x} 與Y-\mu _{y} 的乘積為負值,並不能說明他們反向運動,要結合整體的情況來判斷。
那麽你可能又要問了,既然都是同向變化,那t1時刻X-\mu _{x} 與Y-\mu _{y} 的乘積為負值、其他時刻乘積為正的這種情況,與,t1-t7時刻X-\mu _{x} 與Y-\mu _{y} 的乘積均為正值的情況,到底有什麽差異呢?這點其實前面也解釋過了,差異就是:第一種情況的同向程度不如第二種情況的同向程度大(第一種情況6正1負,第二種情況7正,所以第一種情況的共變異數小於第二種情況的共變異數,第一種情況X,Y變化的同向程度要小於第二種情況)。
另外,如果你還鉆牛角尖,說如果t1,t2,t3……t7時刻X,Y都在增大,而且X都比均值大,Y都比均值小,這種情況共變異數不就是負的了?7個負值求平均肯定是負值啊?但是X,Y都是增大的,都是同向變化的,這不就矛盾了?
這個更好解釋了:這種情況不可能出現!
因為,你的均值算錯了……
X,Y的值應該均勻的分布在均值兩側才對,不可能都比均值大,或都比均值小。
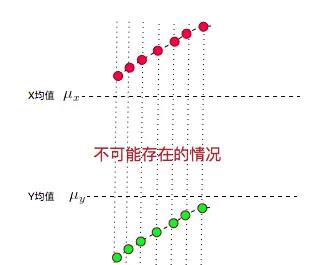
所以,實際它的圖應該是下面這樣的:
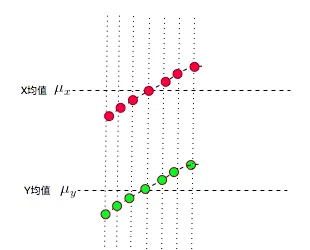
發現沒有,又變成X-\mu _{x} 與Y-\mu _{y} 的符號相同的情況了~有沒有種被大自然打敗的感覺~
好了,現在,對於共變異數應該有點感覺了吧?
二、相關系數:
對於相關系數,我們從它的公式入手。一般情況下,相關系數的公式為:
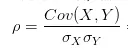
轉譯一下:就是用X、Y的共變異數除以X的標準差和Y的標準差。
所以,相關系數也可以看成共變異數:一種剔除了兩個變量因次影響、標準化後的特殊共變異數。
既然是一種特殊的共變異數,那它:
1、也可以反映兩個變量變化時是同向還是反向,如果同向變化就為正,反向變化就為負。
2、由於它是標準化後的共變異數,因此更重要的特性來了:它消除了兩個變量變化振幅的影響,而只是單純反應兩個變量每單位變化時的相似程度。
比較抽象,下面還是舉個例子來說明:
首先,還是承接上文中的變量X、Y變化的示意圖(X為紅點,Y為綠點),來看兩種情況:
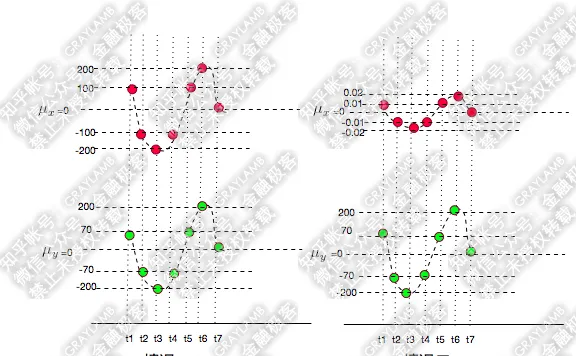
很容易就可以看出以上兩種情況X,Y都是同向變化的,而這個「同向變化」,有個非常顯著特征: X、Y同向變化的過程,具有極高的相似度! 無論第一還是第二種情況下,都是:t1時刻X、Y都大於均值,t2時刻X、Y都變小且小於均值,t3時刻X、Y繼續變小且小於均值,t4時刻X、Y變大但仍小於均值,t5時刻X、Y變大且大於均值……
可是,計算一下他們的共變異數,
第一種情況下:
[(100-0)\times (70-0) +( -100-0)\times ( -70-0)+(-200-0)\times (-200-0)...]\div 7\approx 15428.57
第二種情況下:
[(0.01-0)\times (70-0) +( -0.01-0)\times ( -70-0)+(-0.02-0)\times (-200-0)...]\div 7\approx 1.542857
共變異數差出了一萬倍,只能從兩個共變異數都是正數判斷出兩種情況下X、Y都是同向變化,但是,一點也看不出兩種情況下X、Y的變化都具有相似性這一特點。
這是為什麽呢?
因為以上兩種情況下,在X、Y兩個變量同向變化時,X變化的振幅不同,這樣,兩種情況的共變異數更多的被變量的變化振幅所影響了。
所以,為了能準確的研究兩個變量在變化過程中的相似程度,我們就要把變化振幅對共變異數的影響,從共變異數中剔除掉。於是,相關系數就橫空出世了,就有了最開始相關系數的公式:
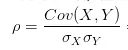
那麽為什麽要透過除以標準差的方式來剔除變化振幅的影響呢?咱們簡單從標準差公式看一下:
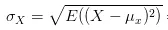
從公式可以看出,標準差計算方法為,每一時刻變量值與變量均值之差再平方,求得一個數值,再將每一時刻這個數值相加後求平均,再開方。
「變量值與變量均值之差」X-\mu _{x} 是什麽呢?就是偏離均值的振幅:
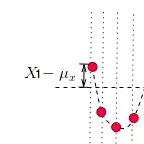
那為何要對它做平方呢?因為有時候變量值與均值是反向偏離的(見下圖),X-\mu _{x} 是個負數,平方後,就可以把負號消除了。這樣在後面求平均時,每一項數值才不會被正負抵消掉,最後求出的平均值才能更好的體現出每次變化偏離均值的情況。
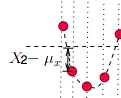
當然,最後求出平均值後並沒有結束,因為剛才為了消除負號,把X-\mu _{x} 進行了平方,那最後肯定要把求出的均值開方,將這個偏離均值的振幅還原回原來的量級。於是就有了下面標準差的公式:
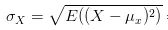
所以標準差描述了變量在整體變化過程中偏離均值的振幅。共變異數除以標準差,也就是把共變異數中變量變化振幅對共變異數的影響剔除掉,這樣共變異數也就標準化了,它反應的就是兩個變量每單位變化時的情況。這也就是相關系數的公式含義了。
同時,你可以反過來想象一下:既然相關系數是共變異數除以標準差,那麽,當X或Y的波動振幅變大的時候,它們的共變異數會變大,標準差也會變大,這樣相關系數的分子分母都變大,其實變大的趨勢會被抵消掉,變小時也亦然。於是,很明顯的,相關系數不像共變異數一樣可以在+\infty 到-\infty 間變化,它只能在+1到-1之間變化(相關系數的取值範圍在+1到-1之間變化可以透過施瓦茨不等式來證明,有些復雜,這裏就不贅述了,有興趣的可以google下)。
總結一下,對於兩個變量X、Y,
當他們的相關系數為1時,說明兩個變量變化時的正向相似度最大,即,你變大一倍,我也變大一倍;你變小一倍,我也變小一倍。也即是完全正相關(以X、Y為橫縱座標軸,可以畫出一條斜率為正數的直線,所以X、Y是線性關系的)。
隨著他們相關系數減小,兩個變量變化時的相似度也變小,當相關系數為0時,兩個變量的變化過程沒有任何相似度,也即兩個變量無關。
當相關系數繼續變小,小於0時,兩個變量開始出現反向的相似度,隨著相關系數繼續變小,反向相似度會逐漸變大。
當相關系數為-1時,說明兩個變量變化的反向相似度最大,即,你變大一倍,我變小一倍;你變小一倍,我變大一倍。也即是完全負相關(以X、Y為橫縱座標軸,可以畫出一條斜率為負數的直線,所以X、Y也是線性關系的)。
有了上面的背景,我們再回到最初的變量X、Y的例子中,可以先看一下第一種情況的相關系數:
X的標準差為
\sigma _{X} =\sqrt{E((X-\mu _{x})^{2} )} =\sqrt{[(100-0)^{2}+ (-100-0)^{2}...]\div 7} \approx 130.9307
Y的標準差為
\sigma _{Y} =\sqrt{E((Y-\mu _{y})^{2} )} =\sqrt{[(70-0)^{2}+ (-70-0)^{2}...]\div 7} \approx 119.2836
於是相關系數為
\rho =15428.57\div (130.9307\times 119.2836)\approx 0.9879
說明第一種情況下,X的變化與Y的變化具有很高的相似度,而且已經接近完全正相關了,X、Y幾乎就是線性變化的。
那第二種情況呢?
X的標準差為
\sigma _{X} =\sqrt{E((X-\mu _{x})^{2} )} =\sqrt{[(0.01-0)^{2}+ (-0.01-0)^{2}...]\div 7} \approx 0.01309307
Y的標準差為
\sigma _{Y} =\sqrt{E((Y-\mu _{y})^{2} )} =\sqrt{[(70-0)^{2}+ (-70-0)^{2}...]\div 7}\approx 119.2836
於是相關系數為
\rho =1.542857\div (0.01309307\times 119.2836)\approx 0.9879
說明第二種情況下,雖然X的變化振幅比第一種情況X的變化振幅小了10000倍,但是絲毫沒有改變「X的變化與Y的變化具有很高的相似度」這一結論。同時,由於第一種、第二種情況的相關系數是相等的,因此在這兩種情況下,X、Y的變化過程有著同樣的相似度。
好了,講了這麽多,不知你看完是否對相關系數也有了一些感覺?
三、寫在最後
本文主要還是想給非理工專業、入門級的各位朋友看的,自己也曾在茫茫公式海中痛苦過,但後來發現對一個公式的原理有了一個感覺後,它也就變得好記很多了,而且也願意深入研究它了。這篇文章也就是培養你對於共變異數、相關系數的這種感覺。但是,為了通俗易懂,有些地方也不夠全面、嚴謹。也許你看完本文,經過自己的學習研究,也會有自己的一些想法,那你可以繼續研究一下本題目下其他答主的答案,透過引入向量、內積等定義,會把共變異數、相關系數說明得更加嚴謹和透徹。總之學習是一個循序漸進的過程,不要覺得徹底明白了什麽,那往往是你踏入一個領域的第一步。
(完)
其他一些推薦的通俗易懂類答案,感興趣的朋友可以閱讀:
作為一個非金融從業者怎樣才能看懂電影【大空頭】? - GRAYLAMB 的回答 - 知乎
關於外匯標價方法的定義,直接標價法到底是什麽? - GRAYLAMB 的回答 - 知乎
如何淺顯易懂地解說 Paxos 的演算法?
未來計劃繼續通俗易懂解讀ApplePay、區塊鏈、機器學習,歡迎關註。
——2017.2.25
關於比特幣與區塊鏈的文章寫好了,有興趣的可以來瞅瞅~
GRAYLAMB:比特幣 (Bitcoin) 系統是如何執行的?
——2017.8.4











