之前鼓起勇氣寫了下面這篇文章。貼出來應該可以回答這個問題,供參考^_^。
簡諧振動是最簡單最基本的振動,它的典型例子是彈簧振子。
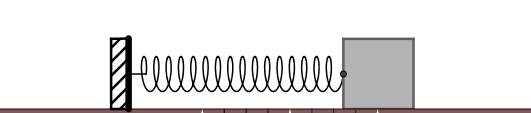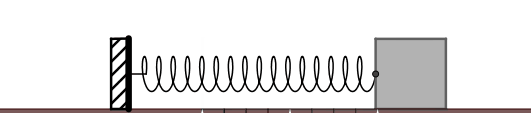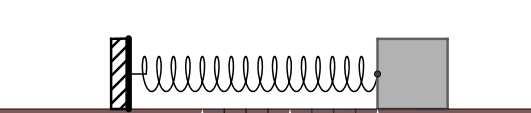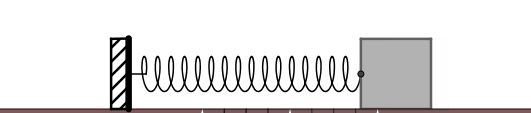
什麽是彈簧振子呢?一個不考慮質素的彈簧連線一個有質素的小球或物塊,然後把它沿著彈簧的方向壓縮或者拉伸一定的距離(不要拉得太狠,悠著點兒)後松手,那麽物塊就會 只在彈簧彈力的作用下,周期性地往復振動 。彈簧振子是一個理想物理模型。振子速度最大的位置回復力為零,此處稱之為 平衡位置 。
在高中我們就知道,彈簧振子的運動學方程式可以表達為如下正弦或余弦函數形式:
\begin{aligned} x(t)=A \cos (\omega t+\varphi)\\ x(t)=A \sin (\omega t+\varphi’) \end{aligned}\\
它們都表述了 振子偏離平衡位置的位移隨時間變化的關系 。由中學數學可知這兩個函數是等價的。 那麽這個振動方程式到底是怎麽推匯出來的呢?
我的書架上有四本書對這個振動方程式有所描述,分別是漆安慎版【力學】、人教社的高中物理教材、【費曼物理學講義】、趙凱華版【新概念物理教程·力學】,外加知乎@烤羚羊的思路。他們 面對同一件事雖然思路迥異,卻又殊途同歸,真真是各有各的特點,各有各的巧妙 。我們一起來看看吧^_^
方式一 「易得」型
這種方式的典型代表是漆老的【力學】,在書中,振動方程式來自於直接寫出微分方程式的解,畫風是下面這這樣的:

為什麽可以寫成這樣呢?當時的我左思右想也沒搞明白這個余弦函數是怎麽來的。漆老可能覺得讀者基本都是大學生了,這等小菜,自己可以推出來。看來我和漆老對大學生的基本要求隔了一個地球周長。所以當時我只是把它當成基本結論去記的。現在,這種處理方式著實不能滿足我對科學的渴望,必須深究下去。
方式二 科學探究型
這種方式的典型代表是現行高中物理人教版教材。從國家到地方都在大力開展新課程改革,要求在物理教學中要重視學生的物理探究過程, 多多體驗一下科學家們發現問題、提出猜想、設計實驗、得出結論、討論驗證等的科學研究過程 。所以人教版高中物理教材是按如下方式得出振動方程式的。
首先, 觀察彈簧振子的頻閃照片 。
讓彈簧振子先振動起來,然後讓頻閃儀對著彈簧振子每隔 0.05s閃光一次,閃光的瞬間振子就會被照亮,從而得到閃光時小球的位置,相鄰兩個位置之間的時間相隔為0.05 s。拍攝時讓底片從左向右勻速運動,因此在底片上留下了小球和彈簧的一系列的像。

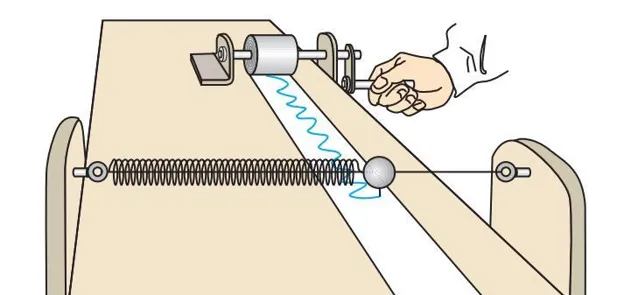
或者,在桌面上放一個彈簧振子(附一支描線筆),下面放上一條長長的寬紙帶,然後在彈簧振子振動的同時在一側把紙帶勻速卷起來,這樣就得到一條和頻閃照片類似的影像。
然後, 猜想影像的函數並驗證 。書上引導讀者猜想這是正弦函數。然後根據振幅和周期寫出正弦函數運算式,再從實驗中得到的影像中選擇幾個點,得到不同時間所得到的位置值,把這個位置值和運算式中對應時間的函數值做個比較。如果符合得很好,說明振動影像就是對應正弦函數。
接著,書上就直接給出了振動方程式,如下圖所示。

人教版高中教材的這個方法簡單直觀,規避了嚴謹的數學推理。其中,把時間作為一個數軸,位移作為另一個數軸,從一維振動中拉一個二維影像的方法是很奇妙的一個思路。
然而,彈簧振子的一維振動,怎麽就跟三角函數扯上了關系呢? 彈簧振子難道就有沒有什麽內在的、固有性質使得它必然與三角函數有關系嗎?
答案顯示不是。 一定是彈簧振子的某些固有內容使得它與三角函數有關系 。那麽我們首先就得找找,彈簧振子到底有哪些固有的內容和規律呢。
彈簧振子的常微分方程式
(如果你時中學生,當你看到常微分方程式這五個字時也許會比較納悶,先不管它,我們來一步步把它給逼出來)
彈簧振子的固有內容
彈簧振子有哪些固有內容會影響到它的振動呢?
首先要想到的性質一定有 物塊的質素 m ,我們可以想想,在彈簧被拉伸的長度一定的前提下,如果物塊越重,那麽振子就應該越「懶」,運動狀態越難得改變,也就是振動得越慢。所以質素m 可能會在振動方程式中體現出來。
接著,我們還應該想到彈簧的 勁度系數 k 也會影響到振動的快慢。如果彈簧越是「硬邦邦」,在彈簧被拉長相同的長度時所具有的拉力越大,物塊受到更大的拉力應該會更快地回到平衡位置。所以勁度系數k 也可能會在振動方程式中體現出來。
有了質素和勁度系數,這只是我們尋找振動方程式的一小步,還需要從彈簧振子必須滿足的內在規律上找。
振子的牛頓第二定律
最先想到的應該是牛頓運動定律。
中學時老師就講,牛頓牛爵爺把力和運動透過 牛頓第二定律 結合起來,小到灰塵,大到天體都可以用它,可以說是相當的厲害。彈簧振子自然也不例外。也就是說,彈簧振子一定滿足F=ma ,其中,F 就是彈簧受到的彈力,a 是振子的加速度。
但是,這和我們尋找的振動方程式有什麽關系呢?牛二定律裏面並沒有出現時間、也沒有出現位移呀。其實,這裏需要一丟丟的微積分知識,利用微積分, 加速度可以表達為位置向量的二階導數 。即可以把牛頓第二定律表達為如下形式:
F= ma = m \frac{\mathrm{d} ^{2}x}{\mathrm{d}{t^2}} \\
如果你沒有微積分方面的數學儲備,推薦你參閱長尾科技的文章【你也能懂的微積分】。
這樣一操作,x 和t 就立馬出現了,似乎答案以經找到了。仔細一想,其實還沒有。你想想看,在振子振動的過程中,彈力總是保持不變的嗎?顯然不是。換句話說, 彈力 F 也會隨著時間,或者說隨著位移發生變化 。如果力F 不隨位移變化還好,我們直接積分就可以得到位移和時間的關系了。可是現在F 並不單純,它裏面還藏著x 或t 沒有露出來,要想直接積分就比較麻煩。
虎克定律
下一步,我們自然要再去找找F 與x 之間有什麽關系。想必你已經知道了,就是牛頓的死對頭虎克發現的 虎克定律 。虎克定律表達為如下形式:
F=-kx \\
虎克定律中有兩點需要註意, 一是它表達了振子離開平衡位置的位移與所受彈力成正比,二是彈力方向始終與位移的方向相反 (前提是我們把振子的平衡位置定義為原點,即位移為0的位置)。
牛頓與虎克的「聯姻」——常微分方程式
接下來,讓人尷尬的一步就出現了。如果我們把虎克定律中表達的F 帶進牛頓第二定律中去,再把常數放在一起,就得到了下面這貨:
\begin{align} \frac{\mathrm{d} ^{2}x}{\mathrm{d}{t^2}}=-\frac{k}{m}x \end{align} \\
在數學中為了更一般的討論,常常把它寫成下面這種形式:
\begin{align} m \frac{\mathrm{d} ^{2}x}{\mathrm{d}{t^2}}+kx=0 \end{align} \\
在數學中,這被稱為 二階常微分方程式 。叫「微分方程式」是因為方程式中有自變量的微商;叫二階是因為微商的階數最高是二階的;叫「常」是因為自變量只有一個(即時間" t ,在數學中,還會出現多變量的情況,這個是後話)。
為什麽說尷尬呢?你瞧瞧,有著恩恩怨怨的牛頓和虎克雖然吵了一輩子,但是他們在科學上的成就卻彼此左手拉右手,至少在描述簡諧振動這件事兒上,別提它們有多甜蜜。
那麽該如何求解這個二階常微分方程式,來得到位移 關於時間的運算式呢?解法其實有很多,真真是八仙過海,各顯神通了。在這裏,我介紹兩種求解方式,一個用的是費曼的推理手法,另一個復數和指數求解的思路。我們一個個地看。
方式三 費曼的推理
費曼是一位擅長 透過簡單的例子去說明高深問題 的大師。比如,1986年,挑戰者號失事後,費曼只用一杯冰水和一只橡皮環,就在國會向公眾揭示了挑戰者失事的根本原因——低溫下橡膠失去彈性。而在彈簧振子的問題上,費曼體現了他的另一個能力—— 面對一個一般問題,先從簡單的情況入手,抓住事物規律的核心,再去考慮其他情況 。

接下來,就讓我們一起,看看費曼是如何推匯出振子位移隨時間變化的振動方程式的。
1. 考慮特殊情況,化簡微分方程式
上面的二階常微分方程式中有兩個常數m 和k ,為分析的方便,我們不妨把m 和k 放到一塊兒,並令k/m=1 ,即假設有這樣一個彈簧振子,它的勁度系數的數值和物塊質素的比值等於1,這個假設顯然是允許的。這樣,沒有常數幹擾的微分方程式就寫成了
\begin{align} \frac{\mathrm{d} ^{2}x}{\mathrm{d}{t^2}}=-x \end{align} \\
至於k/m 不等於1的情況,我們先放一邊兒,過一會兒再考慮它。
2. 抓住微分方程式的關鍵性質嘗試建構函式
不知你發現了沒有,方程式(3)其實表達了這麽一個意思: 關於時間的函數 x ,在經過兩次求導 (即 \frac{\mathrm{d} ^{2}x}{\mathrm{d}{t^2}} ) 後居然變回了自己,還是 x 。只不過多了一個負號 。
到底是什麽樣的函數具有這樣的性質呢?此處迅速在頭腦裏回憶一下初等函數,我們發現,正弦函數或余弦函數都行。不妨設x=\cos(t)\\
3. 根據物理意義最佳化函數的表達
我們知道,時間的單位是"秒",而余弦cos的括弧裏裝著的,應該是以"度"為單位的角度量。因此 括弧裏面不單單是時間 t ,還應該乘上一個量,它與時間的乘積應該是一個角度 。我知道你一定想到了圓周運動的角速度\omega ,因為它乘以時間就是角度。
不過,這裏需要提醒一下,我們需要的這個量雖然與角速度在單位上相同,但是它並不是物體旋轉時的角速度,因為這裏的振子並沒有體現出旋轉的意思。但是我們依然可以把這個量寫成符號\omega_0 。這樣,振動方程式進一步被最佳化成了下面這個樣子:
\begin{align} x(t)=\cos\omega_0t \end{align} \\
這個函數離我們的目標以經很近了,可是 那個 \omega_0 到底是個啥?它有什麽物理意義呢 ?我們還需要進一步探索。
4.把函數嘗試代入微分方程式
為了理解\omega_0 的物理意義,我們把猜測的x=\cos(\omega_0t) 帶入二階常微分方程式中,去看看\omega_0 將會有什麽表現。代入後的結果如下:
\begin{align} \frac{\mathrm{d} ^{2}x}{\mathrm{d}{t^2}}=-\omega_0^{2}x \end{align} \\
透過比較(1)、(5)這兩個式子我們發現,只要令\omega_0^{2}=\frac{k}{m} ,即這兩個式子就相同了。那麽\omega_0=\sqrt{k/m} 。
可以看出, 這個 \omega_0 的確跟彈簧的固有內容有關系,那麽這個關系體現在什麽方面呢?
結合物理情景分析意義
對函數x=\cos\omega_0t ,我們結合實際振動來分析看看。
- 首先振子的位移一定在一個區間內變化,最大值有正負之分,有對稱性,而且最小值為0,余弦函數的取值範圍是(-1,1),也具有對稱性;
- 當時間t=0 時,x 取最大值,這表示振子是從最大位移處開始運動的;
- 振子振動具有周期性,而\cos\omega_0 t 正好是周期函數。
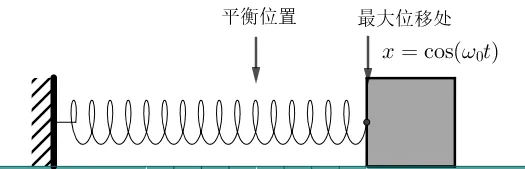
函數的性質與振子的物理性質符合得很好,所以我們有理由相信, 彈簧振子的運動學方程式一定具有余弦函數的內核 。
但是還有個問題, 振子的振動周期,到底等於多少呢 ?
這個問題其實很好回答。我們知道,所謂周期,其實就是物體經過一個時間段T 之後,正好回到出發點。而在余弦函數\cos\theta 中,周期是2\pi 。也就是說,當振子運動了t=T 的時間後,\cos(\omega_0 t) 括弧中所謂的"角度"\omega_0t ,就將等於2\pi 。這樣我們就有\omega_0 T=2\pi ,這樣就求得了周期的運算式為:
\begin{align} T=2\pi\sqrt{\frac{m}{k}} \end{align} \\
這個運算式說明什麽意思呢?
- 表明了當振子質素越大,振動的周期越大,即振子振動得越慢;
- 表明了當彈簧勁度系數越大,振子得周期越小,即振子振動得越快。這和我們上面得討論和實驗規律相吻合。
說到這裏, 對於振子的運動方程式,我們不僅把它的蓋頭掀開了一大半,還順帶求出了彈簧振子的振動周期,還進一步發現了是一個跟周期有關的量,表達了振動的固有內容 。
由特殊到一般,得到通解
透過剛才的分析我們知道,\cos(\omega_0t) 僅僅表達了振子從最大位移處開始運動的情況,此時振子的速度為0,然而, 振子的運動初速度可以不為0啊 。比如本來振子靜止在平衡位置,現在讓一顆子彈射入振子內部,並從此刻開始計時,那麽振子的運動方程式就不再是余弦,而要用正弦。
更進一步想想下這個場景,你正在用秒表去記錄振子的運動,讓秒表指零時為計時起點,此時振子在最大位移處,振動方程式正好是余弦。然後牛頓也帶著秒表走進來,他剛令秒表從零開始計時(假設你的秒表已經走過了\Delta t 的時間),就發現振子在最大位移的一半處。這個時候,對牛頓而言,他在零時刻看到的振子的位置,應該跟你經過了\Delta t 時刻看到的位置是一樣的。因此,牛頓的振動方程式應該寫作:
\cos\omega(t+t_0) \\
由於t_0 是一個任意的數,此時令\varphi =\omega t_0 ,它也是一個任意的數,這樣,方程式可以進一步改成x=\cos(\omega t+\varphi) 。
還有最後一個事兒沒處理幹凈,就是振子的振幅,在上面的運算式中,余弦函數的最大值是1,可是我們可以讓振子以任意的振幅運動,所以,我們還得把振幅A 添加到方程式裏面去。最終,振子的運動學方程式就變成了:
\begin{align} x=A\cos(\omega t+\varphi) \end{align}\\
這就是以彈簧振子為代表的簡諧振動的通解。
方式四 用復變函數的思路
這個思路要感謝知乎大佬 @烤羚羊,他也是從二階常微分方程式入手,在他給出的求解過程一開始和費曼是一樣的,都是先 猜想 解的形式。只不過,費曼猜想的是余弦函數,而@烤羚羊猜想的是e 指數,即e^{\lambda t} ,它和余弦函數一樣,也可以在經歷兩次求導後得到於原函數類似的形式。經過一通推導後,得到了簡諧振動方程式的復數形式如下:
x(t)=r\left[\mathrm{e}^{i(\omega t+\phi)}+\mathrm{e}^{-i(\omega t+\phi)}\right] \\
有興趣的同學可以跳轉到知乎@ 烤羚羊的文章 去看看。
在下一篇文章中,我將從簡諧振動的復數形式出發,去看看怎麽在GeoGebra中把簡諧振動與圓周運動直觀地聯系起來。
方式五 能量守恒大法好
上面的做法總結起來無外乎兩種, 一種是從振子的實驗數據出發,去猜余弦函數 (高中教材的做法), 一種是從振子的動力學方程式出發,去猜常微分方程式的解的可能形式 (費曼的做法和知乎@烤羚羊的做法)。都是 靠猜 。
那有沒有什麽辦法可以不用靠猜,直接透過嚴謹的數學推導就能得出振動方程式呢?有的,就是利用 機械能守恒定律 。這和上面的思路完全不同,【新概念物理學教程·力學】中用的就是這種辦法。我們一起看看吧^_^
彈簧振子具有的能量
為了討論振子的運動學方程式,我們先看看 振子運動過程中的不變量 —— 總能量 。
對於宏觀的彈簧振子而言,總能量無外乎兩種,一種是 振子的動能 ,我們在中學就已經知道它的計算式為\frac{1}{2}mv^2 ,顯然它和振子的速度有關系,而速度是位置的一階導數。另一種是 系統的彈性勢能 U(x) ,那麽彈性勢能的具體運算式又是什麽呢?我麽一起把它搞出來。
彈性勢能的泰勒級數
我以前被泰勒級數這四個字嚇住過,不知道是個什麽玩意兒,隨著認識的加深,我逐漸明白了它的意義——用來近似的。部份讀者可能還蒙在鼓裏。接下來請允許我對它多嘮叨幾句。
首先,我們給出彈性勢能的泰勒級數展示式。為了討論的方便,我們把平衡位置記為0點,那麽偏離平衡位置的位移和振子的位置在數值上相等,這樣,振子的泰勒級數可以表達為如下形式:
U(x)=U(0)+U^{\prime}(0)x+\frac{U^{\prime \prime}(0)}{2 !}x^{2}+\frac{U^{\prime \prime \prime}\left(0\right)}{3 !}(x^{3}+\ldots
大家不要被這麽一長串公式給嚇著,怎麽理解它的意義呢?我們透過分析一副石膏像的素描過程來理解它。

在上圖的素描畫中,第一步先畫出人物的輪廓,雖然它和真實的照片差距很遠,但仍然可以知道這畫了一個人,我把它稱為對真實照片的模擬加入了 一階近似 ;
接著第二步,對人像的五官進行深入勾勒,這時我們發現摩西斯的感覺已經出來了,但還是和真實照片有差距,我把它稱為對真實照片的模擬加入了 二階近似 ;
然後到了第三步,畫家開始對照片中的光影明暗進行深入分析和表現,使得素描畫更加立體豐滿,此時的畫作和真實照片的差距已經很小了。我把這稱為對真實照片的模擬加入了 三階近似 ;
現在你應該明白了, 只要我們不斷地近似下去,讓近似項越來越多,我們對原始物件地表現將會越來越逼真 。
回到泰勒級數上去,它幹的活兒和上面的素描過程其實是一樣的。U(0) 就相當於那一張白紙,U^{\prime}(0)x 就是對彈性勢能加了一階近似,\frac{U^{\prime \prime}(0)}{2 !}x^{2} 就是對彈性勢能加了二階近似,依此類推。
這麽做有什麽好處呢?它可以幫助我們得到彈性勢能的運算式。接下來我們分析一下這些近似的含義和他們的運算式。
1.首先看U(0) ,它表示振子在平衡位置時的彈性勢能。根據對稱性的方便,我們令平衡位置時的彈性勢能為0,即
U(0)=0 \\
2.再看一級近似U^{\prime}(0)x 。這裏有個一階導數U^{\prime}(0) ,它表示什麽意思呢?嘿嘿,在中學我們就學過, 彈簧彈力做的功等於彈性勢能變化量的負值 ,寫成微碎形式就是 F\mathrm{d}x=-\mathrm{d}U 。然後把它變革形,就得到了彈性勢能一階導數的運算式:
U^{\prime}(x)=\frac{\mathrm{d}U}{\mathrm{d}x}=F \\
再根據虎克定律,彈簧彈力大小F=kx ,所以最終我們得到了彈性勢能一階導數為
U^{\prime}(x)=kx \\
而當x=0 時,振子處於平衡位置時的彈力為零,把x=0 帶入上式就得到彈性勢能的一階導數為0。
3.再看彈性勢能的二階導數。有了一階導數的運算式,二階導數自然就可以輕松得到,即
U^{\prime\prime}(x)=k \\
4.最後看高階項。由於二階導數已經為一個常數k 了,那麽三階以上的各項就都等於0了。
終於,彈性勢能的運算式就被我們搞出來了,即
U(x)=\frac{k}{2}x^{2} \\
換元積分求解
有了動能和勢能的運算式,我們就可以得到總的機械能運算式
\begin{align} E=\frac{1}{2}mv^2+\frac{1}{2}kx^2 \end{align}\\
為了等會兒的積分,我們也可以把它改成
\begin{align} v=\sqrt{\frac{2E}{m}(1-\frac{k}{2E}x^2)} \end{align}\\
因為振子振動過程中總能量守恒,所以E 是一個定值常數。為了求解x 隨時間變化的函數,我們寫出速度的導數形式v=\mathrm{d}x/\mathrm{d}t ,那麽有
\begin{align} \frac{\mathrm{d}x}{\sqrt{1-\frac{kx^2}{2E}}}=\sqrt{\frac{2E}{m}}\mathrm{d}t \end{align}\\
接下來就是積分技巧了,我們透過換元法,令\sqrt{k/2E}x=\sin\varphi ,這樣分母
\sqrt{1-\frac{kx^2}{2E}}=\sqrt{1-\sin^2 \varphi}=\cos\varphi \\
而且有
\mathrm{d}x=\sqrt{2E/k}\cos\varphi\mathrm{d}\varphi \\
經過這麽一折騰,上面第3個式子就被改成了
\begin{align} \mathrm{d}\varphi=\sqrt{\frac{k}{m}}\mathrm{d}t \end{align}\\
然後兩邊積分,得到
\begin{align} \varphi=\sqrt{\frac{k}{m}}t+\varphi_0 \end{align}\\
再換元到x ,有
\begin{align} x=\sqrt{2E/k}·\sin(\sqrt{\frac{k}{m}}t+\varphi_0) \end{align}\\
終於大功告成,這個運算式和我們的常見運算式 x(t)=A \sin (\omega t+\varphi’) 在意思上是一樣的。其中的\sqrt{2E/k} 就是振幅A , \sqrt{\frac{k}{m}} 就是我們之前定義那個\omega 。
最後的話
洋洋灑灑六千多字,不算多但也不算少,經過這麽一通分析,我感受到了以下幾點:
- 要想認真學懂一個知識,少不了旁征博引,博覽群書,不要囿於一家之言 。因為一本書有一本書的觀點,它往往會受作者的意圖、篇幅、定位等方面的考慮,不一定面面俱到。
- 把學到的知識寫下來,講給大家聽,會加深、鞏固和檢驗你對知識了解,結交優秀的人 。其實我是一個很自卑的人,很少跟人交流,加上以前視野不開闊,學習不夠深入,對很多知識的認識只是浮於表面。在長尾君的引導下,我逐漸學著去學習,學者寫點東西,把學著把學到的東西講出來。這麽做不僅利己,還能利人,還能借此機會認識更多優秀的人,何樂而不為呢?
關於簡諧振動的方程式,也許還有其它的推導方式,如果你知道的話,歡迎在評論區留言與我分享,讓更多的人知道。











